bzoj 4727: [POI2017]Turysta 图论

        在与Claris谈笑风生和自己的思考后终于学会了竞赛图的哈密顿回路。

       讲道理我以前连竞赛图是啥都不知道。

       首先求出强联通分量+dp是没有疑问的。那么考虑一个强联通分量，有一个结论是竞赛图一定存在哈密顿路径，然后存在哈密顿回路当且仅当强联通。下面给出构造方法。

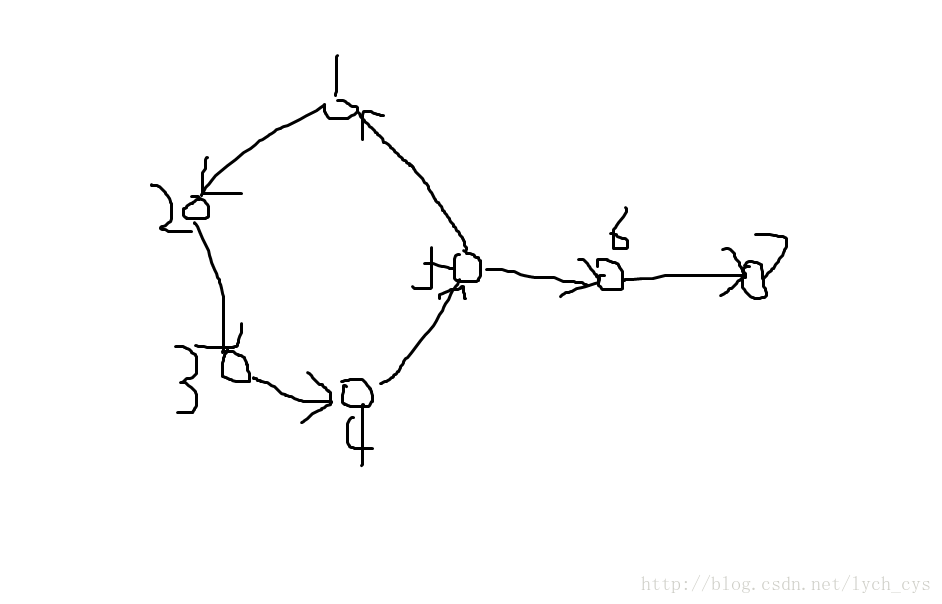
       首先求哈密顿路径（见代码或百度即可）；然后将路径变成环，考虑一个环+一条延伸出去的链，那么要扩大环的大小，分类讨论：

       1.存在边4->6，直接连上即可；

       2.存在边i->6->i+1，用这个替换i->i+1即可；

       3.不存在边6->i(i<=5)，那么在6之后的一条链上一定存在x，使得至少存在x->i(i<=5)，否则就不强联通了。假设存在7->2，那么就变成1->6->7->2->3->4->5->1，其中1->6一定存在因为是竞赛图并且没有边6->1；

       这样就好了，剩下就是一个dp的问题了。

       张姿势了啊~~~

AC代码如下：

#include<bits/stdc++.h>
#define N 2005
using namespace std;

int n,m,cnt,dfsclk,tp,opt_tp,q[N],h[N],nxt[N],pos[N],low[N],scc[N],sz[N],f[N],g[N],p[N];
bool a[N][N],b[N][N],bo[N],vis[N]; char opt_stk[105];
void join(int x){
	int i; vis[x]=1;
	for (i=1; i<=m; i++) if (a[h[i]][x]) bo[h[i]]=1;
}
void work(){
	int head=h[1],tail=h[1],i,j,x,y;
	for (i=2; i<=m; i++){
		x=h[i];
		if (a[x][head]){
			nxt[x]=head; head=x; continue;
		}
		for (j=head,y=0; y!=tail && a[j][x]; y=j,j=nxt[j]);
		if (y==tail){
			nxt[tail]=x; tail=x;
		} else{
			nxt[x]=j; nxt[y]=x;
		}
	}
	int mid=head; join(head);
	while (mid!=tail){
		x=nxt[mid];
		if (a[x][head]){
			mid=x; join(x);
			continue;
		}
		for (i=head; i!=mid && a[i][x]; j=i,i=nxt[i]);
		if (i!=mid){
			nxt[j]=x; nxt[mid]=head;
			mid=x; head=i; join(x);
		} else{
			for (i=1; i<=m; i++) if (bo[h[i]] && !vis[h[i]]) break;
			for (j=head; j!=mid && a[j][h[i]]; j=nxt[j]);
			for (y=nxt[mid]; ; y=nxt[y]){
				join(y);
				if (y==h[i]) break;
			}
			nxt[mid]=head; head=j; mid=h[i];
			for (j=head,i=nxt[head]; i!=head; j=i,i=nxt[i]);
			nxt[j]=x;
		}
	}
	for (i=1; i<=m; i++) bo[h[i]]=vis[h[i]]=0;
	nxt[tail]=head;
}
void dfs(int x){
	int y; pos[x]=low[x]=++dfsclk; q[++tp]=x;
	for (y=1; y<=n; y++) if (a[x][y])
		if (!pos[y]){
			dfs(y); low[x]=min(low[x],low[y]);
		} else if (!scc[y]) low[x]=min(low[x],pos[y]);
	if (pos[x]==low[x]){
		for (p[++cnt]=x,m=0; ;){
			scc[q[tp]]=cnt; h[++m]=q[tp];
			sz[cnt]++;
			if (q[tp--]==x) break;
		}
		work();
	}
}
int dp(int x){
	if (f[x]) return f[x];
	int y,z;
	for (y=1; y<=cnt; y++) if (b[x][y]){
		z=dp(y);
		if (z>f[x]){
			f[x]=z; g[x]=y;
		}
	}
	f[x]+=sz[x]; return f[x];
}
void opt(int x){
	if (!x) putchar('0'); else{
		int y;
		for (; x; x=y){ y=x/10; opt_stk[++opt_tp]='0'+x-y*10; }
		while (opt_tp) putchar(opt_stk[opt_tp--]);
	}
}
void solve(int x){
	if (!x) return;
	int y; putchar(' '); opt(x);
	for (y=nxt[x]; y!=x; y=nxt[y]){
		putchar(' '); opt(y);
	}
	solve(p[g[scc[x]]]);
}
int main(){
	scanf("%d",&n);
	int i,j; char cr;
	for (j=2; j<=n; j++)
		for (i=1; i<j; i++){
			cr=getchar(); while (cr!='0' && cr!='1') cr=getchar();
			a[i][j]=(cr=='1'); a[j][i]=!a[i][j];
		}
	for (i=1; i<=n; i++) if (!pos[i]) dfs(i);
	for (i=1; i<=n; i++)
		for (j=1; j<=n; j++)
			if (scc[i]!=scc[j]) b[scc[i]][scc[j]]|=a[i][j];
	for (i=1; i<=cnt; i++) f[i]=dp(i);
	for (i=1; i<=n; i++){
		printf("%d",f[scc[i]]);
		solve(i); puts("");
	}
	return 0;
}

by lych

2017.1.20