ADC的精度和带宽问题，你知道多少？

今天我们讲ADC的带宽精度，话不多说，直接进入正题↓↓↓

 

ADC建立时间精度

一般而言，一个ADC的内部前端需要在半个周期或采样时钟周期内建立(0.5/Fs)，这样才能提供对内模拟信号捕捉的精确表达。因此，对于一个12位ADC(采样速率为2.5 GSPS，满量程输入范围为1.3 V p-p)来说，全功率带宽(FPBW)可通过下列瞬态公式推导：

求解t：

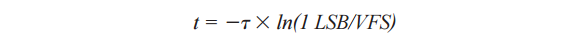代入τ = 1/(2 × π × FPBW)，一个时间常数，求解FPBW：

现在，令t = 0.5/Fs，则样本建立所需的时间如下(样本周期为1/Fs)：

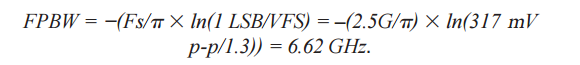这样会使ADC内部前端所需的带宽或FPBW最小。这是转换器内部前端建立至1 LSB以内并正确采样模拟信号所需的带宽。为了满足这类ADC的1 LSB精度要求，这将会需要花费数个时间常数。

 

一个时间常数为24 ps或τ = 1/(2 × π × FPBW)。要了解ADC满量程范围内达到LSB尺寸要求所需的时间常数数量，就需要找出满量程误差或%FS。

 

或者1 LSB = FS/(2N)，其中N = 位数；

或1.3 V p-p/(212) = 317 mV p-p，且%FS = (LSB/FS) × 100 = 0.0244。

 

通过描绘欧拉数或eτ，可以绘出一条曲线，以便每次通过常数都能方便地看出相对误差。如图1可见，12位ADC样本建立至大约1 LSB以内需时8.4个时间常数。

图1.建立精度与时间常数的关系

 

这样，设计人员便能估算用于转换器的最大模拟输入频率或采样带宽，并依旧建立至1 LSB误差以内。超出这个范围，则ADC无法精确表示信号。这可以简单定义为：

 

FMAX = 1/(τ × 时间常数数量)

或

1/(24 ps × 8.4) = 4.96 GHz

 

记住，这里表示的是最佳情形，并假定采用单极点ADC前端。并非所有现实中的转换器都以这种方式工作，但这是一个很好的开端。

 

关于ADC带宽的简要说明

ADC全功率带宽不同于定义的转换器可用带宽或采样带宽，它可以当成是模拟信号输入运算放大器的全功率带宽(FPBW)，信号更像是三角波信号，并且输出端存在大量失真。

 

FPBW是ADC精确捕捉信号并使内部前端正确建立所需的带宽(前文示例中为6.62 GHz)。选择一个IF并在该范围内使用转换器不是一个好主意，因为系统的性能结果会大幅改变；在大约5 GHz处，根据转换器数据手册中的额定分辨率和性能指标，满量程带宽远高于转换器自身的最大采样带宽。

 

设计是围绕采样带宽而展开的。所有设计都应当避免使用额定全功率带宽的某一或全部最高频率部分，否则动态性能(SNR/SFDR)会下降并大幅改变。为了确定高速ADC的采样带宽，应当使用文中的示例，因为这些数据并非总能从数据手册中获取。

 

通常，数据手册会规定甚至列出转换器采样带宽内经过生产测试、能够保证额定性能的频率。然而，在较老的ADC产品中这些测试频率在数据手册中并不总是以FMAX来定义。今后还需要对行业中的这些带宽术语做出更好的说明、定义和测试。