这是一篇翻译 原文:纠错码;
简介
纠错码(RS码)是一种用于纠正错误的信号处理技术。 如今,它们无处不在,例如在通信(移动电话、互联网)、数据存储和存档(硬盘驱动器、光盘 CD/DVD/蓝光、存档磁带)、仓库管理(条形码)和广告(二维码)中。
其中Reed–Solomon 纠错是一种特定类型的纠错码。 它是最古老的算法之一,但仍被广泛使用,因为它的定义非常明确,并且现在在公共领域有几种有效的算法可用。
通常,纠错码是隐藏的,大多数用户甚至不知道它们,也不知道它们何时被使用。 但是,它们是某些应用程序可以正确运行的关键部分,例如通信或数据存储。 事实上,每隔几天就会随机丢失数据的硬盘驱动器将毫无用处,同时只能在理想环境(也就是说网络不存在丢包乱序等)下使用电话交流也是无意思的。但是使用纠错码后就可以将丢失或者损坏的信息恢复为完整的原始消息 。
在上述的使用场景中条形码和 QR 码是值得研究的有趣的应用,因为它们具有直观显示纠错码的特殊性,使好奇的用户可以轻松访问这些代码。
在这篇文章中,我们将尝试从程序员而不是数学家的角度来介绍 Reed-Solomon 码的原理,这意味着我们将更多地关注实践而不是理论,尽管我们也会解释部分理论 ,但只是直观和可执行(代码运行)的必要知识。 同时文中也将提供该领域的著名参考文献,以便感兴趣的读者可以去深入挖掘数学理论。 我们将以目前流行的二维码和条码系统的真实示例以及工作代码示例。 我们选择使用 Python 作为示例(主要是因为它看起来很漂亮并且类似于伪代码),但我们将尝试为不熟悉它的人解释任何不是很好去理解的地方。 文章所涉及的数学是高级的,因此它通常不会在大学水平以下教授,但对于掌握高中代数的人来说应该是可以理解的。
首先我们将去直观的介绍二维码背后的原理,然后在第二部分中我们将介绍二维码的结构设计,即信息如何存储在二维码中以及如何读取和生成它,第三部分我们将通过 Reed-Solomon 解码器的实现来研究纠错码,并快速介绍更大的 BCH 码系列,以便可靠地读取损坏的 QR 码。
请好奇的读者注意,可以在附录和讨论页中找到扩展信息。
1. 纠错原理
在详细介绍代码之前,了解纠错背后的实现可能很有用。 事实上,尽管纠错码在数学上看起来令人生畏,但大多数数学运算都是高中级的(伽罗华域除外,但实际上对任何程序员来说都很简单和常见:它只是对整数进行模数运算 数字)。 然而,纠错码背后的数学独创性的复杂性隐藏了非常直观的目标和机制。
纠错码似乎是一个困难的数学概念,但它们实际上是基于一个直观的想法和巧妙的数学实现:让我们将数据结构化,这样我们就可以通过“修复”结构来“猜测”数据是否被损坏。。 在数学上,我们使用来自伽罗瓦域的多项式来实现这种结构。
让我们做一个更实际的类比:假设您想将消息传达给其他人,但这些消息在此过程中可能会被破坏。纠错码的主要见解是,我们可以使用较小的一组精心挑选的单词,即“精简词典”,而不是使用整个单词词典,以便每个单词都与其他单词一样不同。这样,当我们收到一条消息时,我们只需要在我们的精简字典中查找到 1) 检测哪些单词已损坏(因为它们不在我们的精简字典中); 2)通过在我们的字典中找到最相似的词来纠正损坏的词。
让我们举一个简单的例子:我们有一个只有 4 个字母的三个单词的精简词典:this、that 和 corn。假设我们收到一个损坏的词:co**,其中 * 是擦除。由于我们的字典中只有 3 个单词,因此我们可以轻松地将接收到的单词与我们的字典进行比较,以找到最接近的单词。在这种情况下,它是容易的(corn)。因此丢失的字母是 rn。
现在假设我们收到了单词 th**。这里的问题是我们的字典中有两个词与接收到的词相匹配:this 和 that。在这种情况下,我们无法确定它是哪一个,因此我们无法解码。这意味着我们的字典不是很好,我们应该用另一个更不同的词来代替它,比如破折号,以最大限度地提高每个词之间的差异。这种差异,或者更准确地说是我们字典中任意 2 个单词之间不同字母的最小数量,称为我们字典的最大汉明距离。确保字典中的任意 2 个单词在同一位置仅共享最少数量的字母称为最大可分离性。
大多数纠错码都使用相同的原则:我们只生成一个缩减字典,其中只包含最大可分离性的单词(我们将在第三部分详细介绍如何做到这一点),然后我们只与这个缩减字典中的单词进行通信. Galois Fields 提供的是结构(即简化的字典基础),而 Reed-Solomon 是一种自动创建合适结构的方法(为数据集量身定制具有最大可分离性的简化字典),并提供自动化方法检测并纠正错误(即在精简字典中查找)。更准确地说,Galois Fields(伽罗华域一种有限域])是结构(由于其循环性质,对整数取模),Reed–Solomon(里德-所罗门码) 是基于 Galois Fields 的编解码器(编码器/解码器)。
如果一个词在通信中丢失,那没什么大不了的,因为我们可以通过查看字典并找到最接近的词来轻松修复它,这可能是正确的词(然而,如果输入消息被严重损坏,则有可能选择错误的消息,但概率非常小)。此外,我们的单词越长,它们就越容易分离,因为更多的字符可以在没有任何影响的情况下被破坏。
生成最大可分词词典的最简单方法是使词比实际长度更长。
让我们再次举个例子:
t h i s
t h a t
c o r n
附加一组独特的字符,以便在任何附加位置都没有重复的字符,并再添加一个单词以帮助解释:
t h i s a b c d
t h a t b c d e
c o r n c d e f
请注意,本词典中的每个字与其他字至少相差 6 个字符(t和d相差6个字符),因此距离为 6。这最多允许纠正已知位置(称为擦除)的 5 个错误或未知位置的 3 个错误 .
假设发生 4 次擦除:
t * * * a b * d
然后可以在字典中搜索 4 个未擦除的字符以找到与这 4 个字符匹配的唯一条目,因为距离是 5。这里给出: t h i s a b c d
假设在以下模式之一中发生 2 个错误:
t h o s b c d e
这里的问题是错误的位置未知。 擦除可能发生在任何 2 个位置,这意味着 ( 8 6 ) (_8^6) (86) 或 28 个可能的 6 个字符的子集:
t h o s b c * *
t h o s b * d *
t h o s b * * e
...
如果我们对这些子序列中的每一个进行字典搜索,我们会发现只有一个子集匹配 6 个字符。 t h * * b c d e 匹配 t h a t b c d e。
通过这些示例,可以看出冗余在恢复丢失信息方面的优势:冗余字符可以帮助您恢复原始数据。 前面的例子展示了一个粗略的纠错方案是如何工作的。 Reed–Solomon 的核心思想类似,基于伽罗瓦域数学将冗余数据附加到消息中。 原来的纠错解码器与上面的错误示例类似,在接收到的消息中搜索与有效消息对应的子集,并选择匹配最多的一个作为更正的消息。 这对于较大的消息是不切实际的,因此开发了数学算法以在合理的时间内执行纠错。
2. 二维码结构
本节介绍二维码的结构,即二维码中数据的存储方式。 本节中的信息故意不完整。 此处仅介绍了小尺寸 21×21 尺寸符号(也称为版本 1)的最常见功能,但请参阅附录appendix 以获取更多信息。
这是一个 QR图片,将用作示例。 它由深色和浅色方块组成,在条形码世界中被称为模块。 角落中的三个方形定位器图案是 QR 符号的标识特征。

2.1 掩码
之所以需要掩码处理,是为了避免数据区域中出现诸如类似定位器模式的形状,或者是大片的空白区域等,可能会使扫描器混淆、错乱。掩码处理逆转某些模块(白色变成黑色,黑色变成白色),保留其他模块不变。
屏蔽过程用于避免符号中可能混淆扫描仪的特征,例如看起来像定位器图案和大的空白区域的误导性形状。 掩蔽会反转某些模块(白色变为黑色,黑色变为白色),而让其他模块不受影响。
在下图中,红色区域编码格式信息并使用固定的掩码模式。 数据区域(黑色和白色)用可变图案屏蔽。 创建代码时,编码器会尝试多种不同的掩码,然后选择能够最大限度减少结果中不良特征的掩码。 然后在格式信息中指示所选的掩码模式,以便解码器知道使用哪个。 浅灰色区域是不编码任何信息的固定图案。 除了明显的定位器模式外,还有包含交替明暗模块的计时模式。

使用异或运算(在许多编程语言中由插入符号 ^ 表示)可以轻松应用(或删除)屏蔽转换。 格式信息的取消屏蔽如下所示。 围绕左上角定位器模式逆时针读取,我们有以下位序列。 白色模块代表 0,黑色模块代表 1。
Input 101101101001011
Mask ^ 101010000010010
Output 000111101011001
2.2 格式化信息
有两份相同的格式化信息,以便即使符号损坏,仍然可以对其进行解码。第二份副本分成两部分,分别放置在其他两个定位器周围,并按顺时针方向(在左下角向上,然后在右上角从左到右)读取。
格式化信息的前两位提供了用于消息数据的纠错级别。此大小的QR符号包含26个字节的信息。其中一些用于存储消息,一些用于纠错,如下表所示。左列只是给该级别起的名称。
| 纠错级别 | 级别指示符 Level Indicator | 纠错字节数 | 消息数据字节数 |
|---|---|---|---|
| L | 01 | 7 | 19 |
| M | 00 | 10 | 16 |
| Q | 11 | 13 | 13 |
| H | 10 | 17 | 9 |
格式信息的下三位选择在数据区域中使用的掩模模式。以下是模式的示例,包括告诉模块是黑色还是白色的数学公式(其中i和j分别是行号和列号,并从左上角开始编号为0)。

其余十位格式信息用于纠正格式本身的错误。 这将在后面的部分中解释。
2.3 消息数据
这是一张更大的图表,显示了“未屏蔽”的 QR 码。 指示了符号的不同区域,包括消息数据字节的边界。
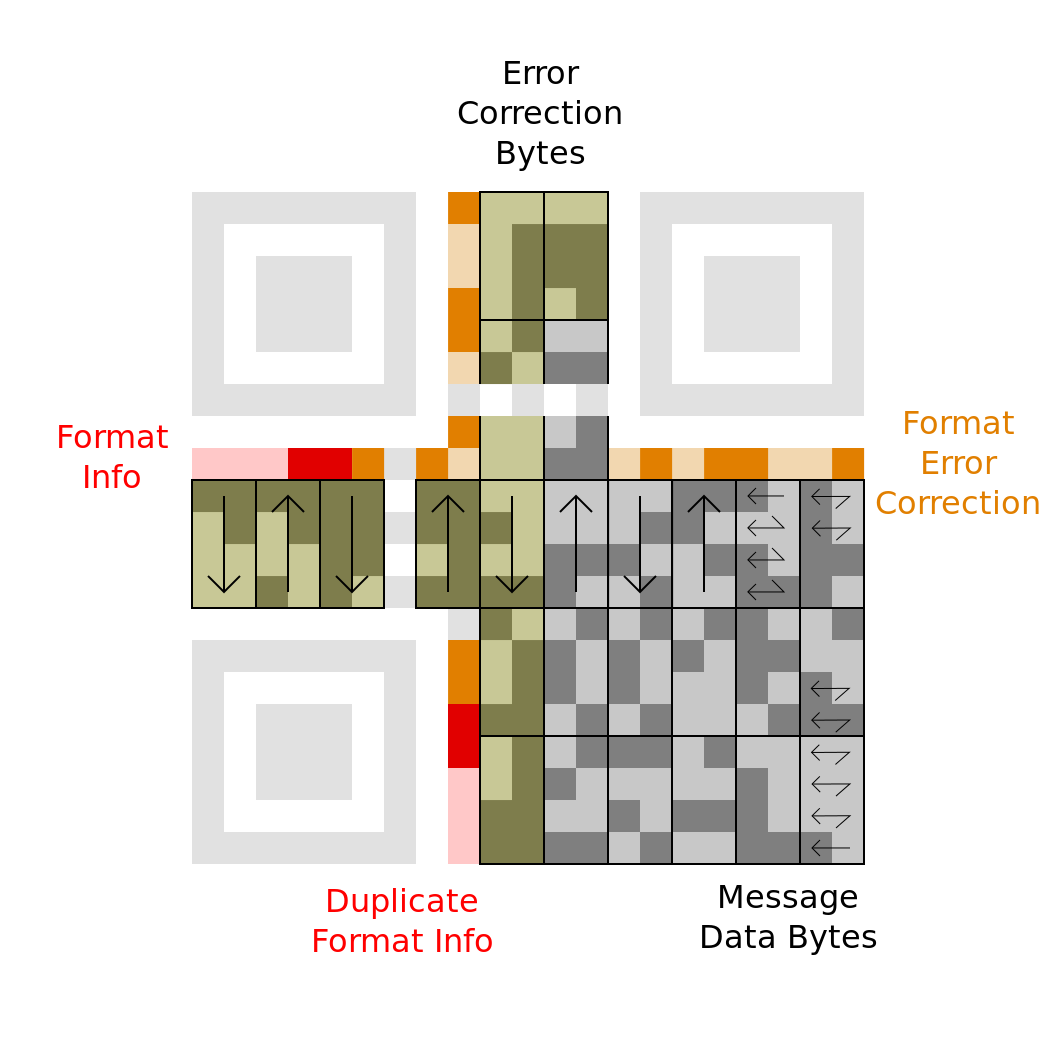
图中数据的读取方式如下:
- 数据位从右下角开始读取,按照之字形的方式依次向上读取右侧两列,首先读取的是01000000 11010010 01110101三个字节。
- 接着,下两列向下读取,因此下一个字节是01000111。
- 当到达底部后,接下来两列将向上读取,以这种上下方式一直读取到符号的左侧(必要时跳过计时图案)。
下面是十六进制符号的完整消息。
- 消息数据字节:
40 d2 75 47 76 17 32 06 27 26 96 c6 c6 96 70 ec - 纠错字节:
bc 2a 90 13 6b af ef fd 4b e0
2.4 解码
最后一步是将消息字节解码为可读的内容,其中前四位指示消息的编码方式。在QR码中会使用多种不同的编码方案,以便可以高效地存储不同种类的消息。下表总结了这些编码方案,在模式指示符之后是一个长度字段,用于说明存储的字符数,长度字段的大小取决于具体的编码方式:
| 模式名称 | 模式指示符 | 长度位 | 数据位 |
|---|---|---|---|
| 数字 | 0001 | 10 | 每3个数字10位 |
| 字母数字混合 | 0010 | 9 | 每2个字符11位 |
| 字节 | 0100 | 8 | 每个字符8位 |
| 汉字 | 1000 | 8 | 每个字符13位 |
(上述长度字段大小仅适用于较小的QR码。)
在上表中,样本消息以0100(十六进制4)开头,表示每个字符有8位,接下来的8位(十六进制0d)是长度字段,十进制为13。之后的位可以重新排列,表示消息的实际字符:27 54 77 61 73 20 62 72 69 6c 6c 69 67,还有0e c。前两个字节,十六进制27和54,是撇号和T的ASCII码。整个消息是“'Twas brillig”(取自w:Jabberwocky#Lexicon)。
在最后一个数据位之后是另一个4位模式指示符。它可能与第一个不同,允许在同一个QR码中混合不同的编码。当没有更多的数据需要存储时,给出特殊的消息结束代码0000。(请注意,如果消息结束代码无法适应可用数据字节数,则标准允许省略消息结束代码。)
此时,我们知道如何解码或读取整个QR码。但是,在实际条件下,QR码很少是完整的:通常,它通过手机相机扫描,在可能存在照明不良的条件下进行扫描,或者在划痕的表面上扫描,其中部分QR码被撕裂,或者在污渍的表面上扫描等等。
为了使我们的QR码解码器可靠,我们需要能够纠正错误。本文的下一部分将描述如何纠正错误,通过构建BCH解码器,更具体地说是一个Reed-Solomon解码器。
3. BCH 编码
在本节中,我们介绍一类通用的纠错码:BCH码,这是现代Reed-Solomon码的母体系。我们还将介绍基本的检测和纠错机制。
格式信息是使用BCH码进行编码的,该码允许检测和纠正一定数量的位错误。BCH码是Reed-Solomon码的一般化(现代的Reed-Solomon码是BCH码)。在QR码的情况下,用于格式信息的BCH码比用于消息数据的Reed-Solomon码要简单得多,因此从BCH码开始讲解是有意义的。
3.1 BCH 错误检测
校验编码信息的过程类似于长除法,但是使用异或运算而不是减法。格式码应该在“除以”该编码的所谓生成器时产生余数为零。QR格式码使用生成器10100110111。下面以示例代码(000111101011001)演示此过程。
0001110100110111 )
000111101011001
^ 101001101110
010100110111
^ 10100110111
00000000000
这里有一个实现这个计算的Python函数。
def qr_check_format(fmt):
g = 0x537 # = 0b10100110111 in python 2.6+
for i in range(4,-1,-1):
if fmt & (1 << (i+10)):
fmt ^= g << i
return fmt
Python注释:对于非Python程序员,range函数可能不太清楚。它产生一个从4到0倒数计数的数字列表(代码中有“-1”,因为“range”返回的间隔包括开始值但不包括结束值)。在C派生的语言中,for循环可能写成for (i = 4; i> = 0; i-);在Pascal衍生的语言中,for i:= 4 downto 0。
Python注释2:&运算符执行按位与,而<<是左位移。这与类C语言一致。
这个函数也可以用来编码5位格式信息。
encoded_format = (format<<10) + qr_check_format(format<<10)
读者可以尝试将此功能推广到除以不同的数字。例如,较大的QR代码包含12个错误纠正位的6位版本信息,使用生成器1111100100101。
在数学形式上,这些二进制数被描述为多项式,其系数是模2的整数。数字的每一位是一个项的系数。例如:
10100110111
=
1
⋅
x
10
+
0
⋅
x
9
+
1
⋅
x
8
+
0
⋅
x
7
+
0
⋅
x
6
+
1
⋅
x
5
+
1
⋅
x
4
+
0
⋅
x
3
+
1
⋅
x
2
+
1
⋅
x
+
1
=
x
10
+
x
8
+
x
5
+
x
4
+
x
2
+
x
+
1
10100110111 = 1\cdot x^{10} + 0\cdot x^9 + 1\cdot x^8 + 0\cdot x^7 + 0\cdot x^6 + 1\cdot x^5 + 1\cdot x^4 + 0\cdot x^3 + 1\cdot x^2 + 1\cdot x + 1 = x^{10} + x^8 + x^5 + x^4 + x^2 + x + 1
10100110111=1⋅x10+0⋅x9+1⋅x8+0⋅x7+0⋅x6+1⋅x5+1⋅x4+0⋅x3+1⋅x2+1⋅x+1=x10+x8+x5+x4+x2+x+1
如果qr_check_format产生的余数不为零,则代码已经损坏或读取错误。下一步是确定哪个格式代码最可能是预期的代码(即在我们的缩小的字典中查找)。
3.2 BCH错误纠正
虽然解码BCH代码的复杂算法存在,但在这种情况下它们可能是过度的。由于只有32个可能的格式代码,因此更容易的方法是尝试每个代码并选择与问题代码不同的最小位数的代码(不同位数的数量称为汉明距离)。查找最接近代码的方法称为穷举搜索,只有因为我们有很少的代码(代码是有效消息,在这里只有32个,所有其他二进制数都不正确)。
(请注意,Reed-Solomon也基于这个原则,但由于可能的编码字数太大,我们负担不起进行穷举搜索,这就是为什么已经设计了聪明但复杂的算法,例如Berlekamp-Massey。)
def hamming_weight(x):
weight = 0
while x > 0:
weight += x & 1
x >>= 1
return weight
def qr_decode_format(fmt):
best_fmt = -1
best_dist = 15
for test_fmt in range(0,32):
test_code = (test_fmt<<10) ^ qr_check_format(test_fmt<<10)
test_dist = hamming_weight(fmt ^ test_code)
if test_dist < best_dist:
best_dist = test_dist
best_fmt = test_fmt
elif test_dist == best_dist:
best_fmt = -1
return best_fmt
函数 qr_decode_format 如果无法解码格式代码,则返回-1。当两个或更多格式代码与输入的距离相同时,就会发生这种情况。
要在Python中运行此代码,首先启动IDLE,Python的集成开发环境。您应该会看到一个版本消息和交互式输入提示符>>>。打开一个新窗口,将函数qr_check_format、hamming_weight和qr_decode_format复制到其中,并保存为qr.py。返回提示符>>>之后依次输入面的行。
>>> from qr import *
>>> qr_decode_format(int("000111101011001",2)) # no errors
3
>>> qr_decode_format(int("111111101011001",2)) # 3 bit-errors
3
>>> qr_decode_format(int("111011101011001",2)) # 4 bit-errors
-1
当然也可以在命令提示符下键入python来启动Python。
在接下来的章节中,我们将研究有限域算术和Reed-Solomon代码,它是BCH代码的一个子类型。基本思想(即使用具有最大可分离性的有限字典)是相同的,但由于我们将编码更长的字(256个字节而不是2个字节),具有更多可用符号(编码在所有8位上,因此有256种不同的可能值),因此我们不能使用这种朴素、穷举的方法,因为这将花费太多时间:我们需要使用更聪明的算法,有限域数学将帮助我们做到这一点,给我们提供一个结构。
4. 有限域算法
4.1 数学领域介绍
在讨论用于消息的Reed-Solomon编码之前,介绍一些更多的数学知识会很有用。
我们希望为8位字节定义加法、减法、乘法和除法,并始终产生8位字节作为结果,以避免任何溢出。天真地说,我们可以尝试使用这些操作的普通定义,然后对256取模,以防止结果溢出。这正是我们将要做的事情,也被称为Galois域2^8。你可以很容易地想象为什么它适用于所有操作,除了除法:5/4是多少?
这里简要介绍一下Galois域:有限域是一组数字,而一个域需要具有六个属性来规定加法、减法、乘法和除法:闭合性、结合性、交换律、分配律、单位元和逆元。更简单地说,使用一个域可以让我们研究该域中的数字之间的关系,并将结果应用于遵循相同属性的任何其他域。例如,实数集ℝ就是一个域。换句话说,数学域研究了一组数字的结构。
但是,整数ℤ不是一个域,因为如上所述,不是所有的除法都被定义了(比如5/4),这违反了乘法逆元的属性(不存在x使得x4=5)。修复它的一种简单方法是使用模数,使用质数,例如257,或任何质数的正整数幂:这样,我们保证x4=5存在,因为我们只需循环回来。ℤ模任何质数被称为Galois域,而模2是一个额外有趣的Galois域:因为一个8位字符串可以表示总共256=2^8个值,所以我们说我们使用2^8的Galois域,或GF(2^8)。在口语中,2是域的特征,8是指数,256是域的基数。有关有限域的更多信息可以在这里找到。
在这里,我们将定义通常使用整数进行的数学操作,但是改为适用于GF(2^8),这基本上是在2^8模下执行常规操作。
另一种考虑GF(2)和GF(2^8)之间的联系的方法是认为GF(2^8)代表8个二进制系数的多项式。例如,在GF(2^8)中,170等价于10101010 = 1*x^7 + 0*x^6 + 1*x^5 + 0*x^4 + 1*x^3 + 0*x^2 + 1*x + 0 = x^7 + x^5 + x^3 + x.。这两种表示是等价的,只是在第一种情况下,这两种表示法是等价的,只是在第一种情况下,170的表示是十进制的,而在另一种情况下,它是二进制的,可以想象为按照约定表示多项式(仅在GF(2 ^ p)中使用,如此处所述)。后者通常是学术书籍和硬件实现中使用的表示法(因为逻辑门和寄存器在二进制级别上工作)。对于软件实现,可以优先选择十进制表示法,以获得更清晰、更接近数学代码的效果(这是本教程中将使用的表示方法,除了一些将使用二进制表示法的示例)。
无论如何,要注意不要混淆表示单个GF(2 ^ p)符号的多项式(每个系数都是位/布尔值:要么为0,要么为1),以及表示GF(2 ^ p)符号列表的多项式(在这种情况下,多项式相当于消息+RS码,每个系数是0到2 ^ p之间的值,代表消息+RS码的一个字符)。我们将首先描述单个符号的运算,然后是一系列符号的多项式运算。
4.2 加和减 (Addition and Subtraction)
在以 2 为底的伽罗华域中,加法和减法都被异或替换。这是合乎逻辑的:加法模 2 与异或完全相同,减法模 2 与加法模 2 完全相同。这是因为在这个伽罗瓦域中,加法和减法都没有进位的概念。
我们可以将8位值看作系数模2的多项式:
0101 + 0110 = 0101 - 0110 = 0101 XOR 0110 = 0011
相同的方式(以两个单个 GF(2^8) 整数的二进制表示):
(
x
2
+
1
)
+
(
x
2
+
x
)
=
2
x
2
+
x
+
1
=
0
x
2
+
x
+
1
=
x
+
1
( x^{2} + 1) + (x^{2} + x) = 2 x^{2} + x + 1 = 0 x^{2} + x + 1 = x + 1
(x2+1)+(x2+x)=2x2+x+1=0x2+x+1=x+1
由于 (a ^ a) = 0,每个数字都是它自己的相反数,所以 (x - y) 与 (x + y) 相同。
请注意,在文中,您会发现加法和减法定义了一些对 GF 整数的数学运算,但实际上,您可以只进行 XOR(只要您处于基数为 2 的伽罗瓦域;在其他域中则不然)。
这是等效的 Python 代码:
def gf_add(x, y):
return x ^ y
def gf_sub(x, y):
return x ^ y # in binary galois field, subtraction is just the same as addition (since we mod 2)
4.3 乘法(Multiplication)
乘法同样基于多项式乘法。 只需将输入写成多项式,然后像往常一样使用分配律将它们相乘。 例如,10001001 乘以 00101010 计算如下:
(
x
7
+
x
3
+
1
)
(
x
5
+
x
3
+
x
)
=
x
7
(
x
5
+
x
3
+
x
)
+
x
3
(
x
5
+
x
3
+
x
)
+
1
(
x
5
+
x
3
+
x
)
=
x
12
+
x
10
+
2
x
8
+
x
6
+
x
5
+
x
4
+
x
3
+
x
=
x
12
+
x
10
+
x
6
+
x
5
+
x
4
+
x
3
+
x
(x^{7} + x^{3} + 1) (x^{5} + x^{3} + x) = x^{7} (x^{5} + x^{3} + x) + x^{3} (x^{5} + x^{3} + x) + 1 (x^{5} + x^{3} + x) = x^{12} + x^{10} + 2 x^{8} + x6 + x^{5} + x^{4} + x^{3} + x = x^{12} + x^{10} + x^{6} + x^{5} + x^{4} + x^{3} + x
(x7+x3+1)(x5+x3+x)=x7(x5+x3+x)+x3(x5+x3+x)+1(x5+x3+x)=x12+x10+2x8+x6+x5+x4+x3+x=x12+x10+x6+x5+x4+x3+x
可以通过标准小学乘法程序的修改版本获得相同的结果,其中我们将加法替换为异或。
10001001
* 00101010
10001001
^ 10001001
^ 10001001
1010001111010
注意:这里的异或乘法是没有进位的!如果你使用了带进位的异或乘法,你将会得到错误的结果1011001111010,而不是正确的结果1010001111010。
这是一个在单个GF(2 ^ 8)整数上实现此多项式乘法的Python函数。
注意:这个函数(以及下面的一些其他函数)使用了很多位运算符,比如>>和<<,因为它们在做我们想做的事情时既快又简洁。这些运算符在大多数编程语言中都可以使用,它们不是特定于Python的,你可以在这里获取更多关于它们的信息。
def cl_mul(x,y):
'''Bitwise carry-less multiplication on integers'''
z = 0
i = 0
while (y>>i) > 0:
if y & (1<<i):
z ^= x<<i
i += 1
return z
当然,结果不再适合于8位字节(在这个例子中,它有13位长),因此我们需要在完成之前再执行一步操作。结果被模除100011101(这个数字的选择在代码下面解释),使用之前描述过的长除法过程。在这种情况下,这被称为“模约简”,因为基本上我们所做的就是除法并只保留余数,使用了一个模。这在我们的例子中产生了最终答案11000011。
1010001111010
^ 100011101
0010110101010
^ 100011101
00111011110
^ 100011101
011000011
以下是执行整个伽罗瓦域乘法和模约简的Python代码:
def gf_mult_noLUT(x, y, prim=0):
'''在不使用预先计算的查找表的情况下在伽罗瓦域中进行乘法(因此速度较慢)
通过使用标准的无进位乘法 + 使用不可约素多项式的模约简'''
### 将按位无进位操作定义为内部函数 ###
def cl_mult(x,y):
'''Bitwise carry-less multiplication on integers'''
z = 0
i = 0
while (y>>i) > 0:
if y & (1<<i):
z ^= x<<i
i += 1
return z
def bit_length(n):
'''Compute the position of the most significant bit (1) of an integer. Equivalent to int.bit_length()'''
bits = 0
while n >> bits: bits += 1
return bits
def cl_div(dividend, divisor=None):
'''Bitwise carry-less long division on integers and returns the remainder'''
# Compute the position of the most significant bit for each integers
dl1 = bit_length(dividend)
dl2 = bit_length(divisor)
# If the dividend is smaller than the divisor, just exit
if dl1 < dl2:
return dividend
# Else, align the most significant 1 of the divisor to the most significant 1 of the dividend (by shifting the divisor)
for i in range(dl1-dl2,-1,-1):
# Check that the dividend is divisible (useless for the first iteration but important for the next ones)
if dividend & (1 << i+dl2-1):
# If divisible, then shift the divisor to align the most significant bits and XOR (carry-less subtraction)
dividend ^= divisor << i
return dividend
### Main GF multiplication routine ###
# Multiply the gf numbers
result = cl_mult(x,y)
# Then do a modular reduction (ie, remainder from the division) with an irreducible primitive polynomial so that it stays inside GF bounds
if prim > 0:
result = cl_div(result, prim)
return result
运行结果:
>>> a = 0b10001001
>>> b = 0b00101010
>>> print bin(gf_mult_noLUT(a, b, 0)) # multiplication only
0b1010001111010
>>> print bin(gf_mult_noLUT(a, b, 0x11d)) # multiplication + modular reduction
0b11000011
为什么要使用模数100011101(十六进制:0x11d)?这里的数学有点复杂,但简而言之,100011101表示一个“不可约”(意味着它不能表示为两个较小的多项式的乘积)的8次多项式。这个数字被称为原始多项式、不可约多项式或素多项式(本教程的其余部分主要使用后者的名称)。这对于除法的行为良好是必要的,也就是保持在伽罗瓦域的限制之内,但不会重复值。我们可以选择其他数字,但它们本质上都是相同的,而100011101(0x11d)是Reed-Solomon编码的常见素多项式。如果您想知道如何生成这些素多项式,请参见附录。
关于素多项式的其他信息(您可以跳过):什么是素多项式?它是在伽罗瓦域中的一个等价于质数的概念。请记住,伽罗瓦域使用2的倍数作为生成器。当然,在标准算术中,质数不能是2的倍数,但在伽罗瓦域中是可能的。为什么需要素多项式?因为为了保持在域的边界内,我们需要对域以上的任何值进行模运算。为什么不能直接用域的大小来取模?因为我们最终会得到许多重复的值,我们希望在域中有尽可能多的唯一值,以便在进行模运算或使用素多项式进行异或运算时,数字始终只有一个并且仅有的投影。
对于有兴趣的读者的注释:作为使用巧妙算法可以实现的示例,这里是一种使用俄罗斯农民乘法算法以更简洁、更快速的方式实现GF数乘法的方法:
def gf_mult_noLUT(x, y, prim=0, field_charac_full=256, carryless=True):
'''使用 Russian Peasant Multiplication 算法的 Galois Field 整数乘法(比标准乘法 + 模归约更快)。
如果 prim 为 0 且 carryless=False,则该函数生成标准整数乘法的结果(无进位算术或模归约).'''
r = 0
while y: # while y is above 0
if y & 1: r = r ^ x if carryless else r + x # 如果y是奇数,则将对应的x添加到r中(对于所有奇数y对应的x的总和将给出最终乘积)。请注意,由于我们处于GF(2)中,因此添加实际上是一个异或操作(非常重要,因为在GF(2)中,乘法和加法是无进位的,因此它会改变结果!)。
y = y >> 1 # equivalent to y // 2
x = x << 1 # equivalent to x*2
if prim > 0 and x & field_charac_full: x = x ^ prim # GF 模:如果 x >= 256,则使用本原多项式应用模约简(我们只是减去,但由于本原数可以大于 256,因此我们直接异或)。
return r
注意*,使用此最后一个函数并将参数 prim=0 和 carryless=False,将返回标准整数乘法的结果(因此您可以看到有/无进位加法之间的区别及其对乘法的影响)。*
4.3 乘以对数
上面所描述的过程不是实现 Galois 域乘法最方便的方式。将两个数相乘需要执行多达八次乘法循环,然后执行多达八次除法循环。但是,我们可以使用查找表来实现无循环乘法。一种解决方案是在内存中构建整个乘法表,但那需要一个庞大的 64k 表。下面所描述的解决方案要紧凑得多。
首先,注意到用 2=00000010(按照惯例,这个数字被称为 α 或生成器数字)乘以一个数特别容易:只需要将这个数左移一位,然后如果必要,使用模数 100011101 进行异或运算(为什么异或运算足以在这种情况下进行模运算是留给读者的练习题),下面是前几个 α 的幂:
| α 0 = 00000001 α^{0}= 00000001 α0=00000001 | α 4 = 00010000 α^{4} = 00010000 α4=00010000 | α 8 = 00011101 α^{8} = 00011101 α8=00011101 | α 12 = 11001101 α^{12} = 11001101 α12=11001101 |
| α 1 = 00000010 α^{1} = 00000010 α1=00000010 | α 5 = 00100000 α^{5} = 00100000 α5=00100000 | α 9 = 00111010 α^{9} = 00111010 α9=00111010 | α 13 = 10000111 α^{13} = 10000111 α13=10000111 |
| α 2 = 00000100 α^{2} = 00000100 α2=00000100 | α 6 = 01000000 α^{6}= 01000000 α6=01000000 | α 10 = 01110100 α^{10} = 01110100 α10=01110100 | α 14 = 00010011 α^{14} = 00010011 α14=00010011 |
| α 3 = 00001000 α^{3} = 00001000 α3=00001000 | α 7 = 10000000 α^{7}= 10000000 α7=10000000 | α 11 = 11101000 α^{11}= 11101000 α11=11101000 | α 15 = 00100110 α^{15}= 00100110 α15=00100110 |
如果这个表按照同样的方式继续下去,α的幂不会重复,直到α255 = 00000001。因此,除零元素外,域中的每个元素都等于α的某个幂次。我们定义的元素α被称为Galois域的原始元素或生成元。
这个观察结果暗示了另一种实现乘法的方法:通过将α的指数相加。
10001001
∗
00101010
=
α
74
∗
α
142
=
α
74
+
142
=
α
216
=
11000011
10001001 * 00101010 = α^{74} * α^{142} = α^{74} + 142 = α^{216} = 11000011
10001001∗00101010=α74∗α142=α74+142=α216=11000011
问题是,我们如何找到对应于 10001001 的 α 的幂?这被称为离散对数问题,没有有效的一般解法。然而,由于这个域中只有256个元素,我们可以很容易地构造一个对数表。顺便说一句,相应的反对数表(指数函数)也会很有用,有关这种技巧的更多数学信息可以在这里找到:
gf_exp = [0] * 512 # Create list of 512 elements. In Python 2.6+, consider using bytearray
gf_log = [0] * 256
def init_tables(prim=0x11d):
'''使用提供的原始多项式预先计算对数和反对数表,以便稍后进行更快的计算.'''
# prim is the primitive (binary) polynomial. Since it's a polynomial in the binary sense,
# it's only in fact a single galois field value between 0 and 255, and not a list of gf values.
global gf_exp, gf_log
gf_exp = [0] * 512 # anti-log (exponential) table
gf_log = [0] * 256 # log table
# For each possible value in the galois field 2^8, we will pre-compute the logarithm and anti-logarithm (exponential) of this value
x = 1
for i in range(0, 255):
gf_exp[i] = x # compute anti-log for this value and store it in a table
gf_log[x] = i # compute log at the same time
x = gf_mult_noLUT(x, 2, prim)
# If you use only generator==2 or a power of 2, you can use the following which is faster than gf_mult_noLUT():
#x <<= 1 # multiply by 2 (change 1 by another number y to multiply by a power of 2^y)
#if x & 0x100: # similar to x >= 256, but a lot faster (because 0x100 == 256)
#x ^= prim # substract the primary polynomial to the current value (instead of 255, so that we get a unique set made of coprime numbers), this is the core of the tables generation
# Optimization: double the size of the anti-log table so that we don't need to mod 255 to
# stay inside the bounds (because we will mainly use this table for the multiplication of two GF numbers, no more).
for i in range(255, 512):
gf_exp[i] = gf_exp[i - 255]
return [gf_log, gf_exp]
Python注释:range操作符的上限是不包括的,因此gf_exp[255]不会在上述操作中设置两次。
gf_exp表格的大小超出了实际需要,这是为了简化乘法函数。这样,我们不需要检查gf_log[x] + gf_log[y]是否在表格大小范围内。
def gf_mul(x,y):
if x==0 or y==0:
return 0
return gf_exp[gf_log[x] + gf_log[y]] # should be gf_exp[(gf_log[x]+gf_log[y])%255] if gf_exp wasn't oversized
Division
Another advantage of the logarithm table approach is that it allows us to define division using the difference of logarithms. In the code below, 255 is added to make sure the difference isn't negative.
def gf_div(x,y):
if y==0:
raise ZeroDivisionError()
if x==0:
return 0
return gf_exp[(gf_log[x] + 255 - gf_log[y]) % 255]
Python 注意事项:raise 语句抛出异常并中止 gf_div 函数的执行。
这个定义的除法满足gf_div(gf_mul(x,y),y)==x,对于任何非零的y和x。
对于更高级的程序员来说,编写一个封装了Galois field算术的类可能会很有趣。可以使用操作符重载来替换对gf_mul和gf_div的调用,使用乘法符号*和除法符号/,但是这可能会导致混淆,因为不知道正在执行哪种类型的操作。某些细节可以泛化,以使该类更加广泛地适用。例如,Aztec码使用五种不同的Galois field,元素大小范围从4位到12位不等。
4.4 幂和逆元
对于计算幂和逆元,对数表方法将再次简化和加速我们的计算:
def gf_pow(x, power):
return gf_exp[(gf_log[x] * power) % 255]
def gf_inverse(x):
return gf_exp[255 - gf_log[x]] # gf_inverse(x) == gf_div(1, x)
多项式
在继续介绍Reed-Solomon码之前,我们需要定义多项式上的几个操作,它们的系数是Galois域的元素。这可能会引起混淆,因为元素本身被描述为多项式;我的建议是不要过多思考。增加混淆的是,x仍然用作占位符。这个x与之前提到的x没有任何关系,所以不要混淆它们。
之前用于Galois域元素的二进制表示法在这一点上开始变得不方便,因此我将改用十六进制表示法。
00000001
x
4
+
00001111
x
3
+
00110110
x
2
+
01111000
x
+
01000000
=
01
x
4
+
0
f
x
3
+
36
x
2
+
78
x
+
40
00000001 x^{4} + 00001111 x^{3} + 00110110 x^{2} + 01111000 x + 01000000 = 01 x^{4} + 0f x^{3} + 36 x^{2} + 78 x + 40
00000001x4+00001111x3+00110110x2+01111000x+01000000=01x4+0fx3+36x2+78x+40
在Python中,多项式将由数字列表表示,按x的幂降序排列,因此上面的多项式变为[ 0x01,0x0f,0x36,0x78,0x40 ]。(反向顺序也可以使用;两种选择都有其优点和缺点。)
第一个函数将一个多项式乘以一个标量。
def gf_poly_scale(p,x):
r = [0] * len(p)
for i in range(0, len(p)):
r[i] = gf_mul(p[i], x)
return r
注意:对于Python程序员,这个函数的编写风格不太符合"Pythonic"。它可以用列表推导式来优雅地表达,但我限制自己使用更容易转化为其他编程语言的语言特性。
该函数将两个多项式相加(通常使用异或操作):
def gf_poly_add(p,q):
r = [0] * max(len(p),len(q))
for i in range(0,len(p)):
r[i+len(r)-len(p)] = p[i]
for i in range(0,len(q)):
r[i+len(r)-len(q)] ^= q[i]
return r
下一个函数将两个多项式相乘:
def gf_poly_mul(p,q):
'''Multiply two polynomials, inside Galois Field'''
# Pre-allocate the result array
r = [0] * (len(p)+len(q)-1)
# Compute the polynomial multiplication (just like the outer product of two vectors,
# we multiply each coefficients of p with all coefficients of q)
for j in range(0, len(q)):
for i in range(0, len(p)):
r[i+j] ^= gf_mul(p[i], q[j]) # equivalent to: r[i + j] = gf_add(r[i+j], gf_mul(p[i], q[j]))
# -- you can see it's your usual polynomial multiplication
return r
最后,我们需要一个函数来计算特定 x 值处的多项式,从而产生标量结果。 Horner 方法用于避免显式计算 x 的幂。 Horner 的方法通过连续分解项来工作,因此我们总是迭代地处理 x^1,避免计算更高阶的项:
01
x
4
+
0
f
x
3
+
36
x
2
+
78
x
+
40
=
(
(
(
01
x
+
0
f
)
x
+
36
)
x
+
78
)
x
+
40
01 x^{4} + 0f x^{3} + 36 x^{2} + 78 x + 40 = (((01 x + 0f) x + 36) x + 78) x + 40
01x4+0fx3+36x2+78x+40=(((01x+0f)x+36)x+78)x+40
def gf_poly_eval(poly, x):
'''Evaluates a polynomial in GF(2^p) given the value for x. This is based on Horner's scheme for maximum efficiency.'''
y = poly[0]
for i in range(1, len(poly)):
y = gf_mul(y, x) ^ poly[i]
return y
我们还需要一项缺失的多项式运算:多项式除法。 这比多项式的其他运算更复杂,因此我们将在下一章中与 Reed–Solomon 编码一起研究它。
5. Reed–Solomon 编码
现在,我们可以开始学习 Reed-Solomon 码了,前置知识已经讲完了。
5.1 编码理论的启示
但首先,为什么我们需要学习有限域和多项式?因为这是像 Reed-Solomon 这样的纠错码的主要启示:我们不仅将消息视为一系列(ASCII)数字,而是将其视为遵循有限域算术非常明确定义规则的多项式。换句话说,通过使用多项式和有限域算术来表示数据,我们为数据添加了一个结构。消息的值仍然是相同的,但是这个概念性的结构现在允许我们根据明确定义的数学规则在消息上操作其字符值。这个结构,我们总是知道的,因为它独立于数据之外,并且这正是让我们修复受损消息的原因。
因此,即使在您的代码实现中,您选择不显式表示多项式和有限域算术,这些概念对于纠错码的工作至关重要,而且您将发现这些概念在任何实现中都有所涵盖(即使是隐式)。
现在,我们将把这些概念付诸实践!
5.2 RS 编码
5.2.1 编码概述
与BCH码类似,Reed-Solomon码的编码是通过将表示消息的多项式除以一个不可约生成多项式来完成的,然后余数就是RS码,我们将其附加到原始消息后面。
为什么这么做?我们之前说过,BCH码和大多数其他纠错码的原理是使用具有非常不同单词的缩小字典,以最大化单词之间的距离,而较长的单词具有更大的距离:这里也是同样的原理,首先因为我们用额外的符号(余数)扩展了原始消息,从而提高了距离,其次因为余数几乎是唯一的(由于精心设计的不可约生成多项式),所以可以通过聪明的算法来推断出原始消息的部分内容。
总之,可以类比加密:我们的生成多项式是我们的编码字典,多项式除法是操作符,用生成多项式将消息转换为RS码。
5.2.2 异常管理
为了处理错误和无法纠正消息的情况,我们将显示一个有意义的错误消息,通过引发异常。我们将制作自己的自定义异常,以便用户可以轻松地捕获和处理它们:
为了管理我们无法更正消息的错误和情况,我们将通过引发异常来显示有意义的错误消息。 我们将创建自己的自定义异常,以便用户可以轻松捕获和管理它们:
class ReedSolomonError(Exception):
pass
要通过引发我们的自定义异常来显示错误,我们可以简单地执行以下操作:
raise ReedSolomonError("Some error message")
您可以使用 try/except 块轻松捕获此异常以对其进行管理:
try:
raise ReedSolomonError("Some error message")
except ReedSolomonError as e:
pass # do something here
5.2.3 RS 生成多项式
Reed-Solomon码使用与BCH码类似的生成多项式(注意不要混淆生成数alpha)。生成多项式是因子(x - αn)的乘积,对于QR码来说,从n=0开始,例如: g 4 ( x ) = ( x − α 0 ) ( x − α 1 ) ( x − α 2 ) ( x − α 3 ) g4(x) = (x - α^{0}) (x - α^{1}) (x - α^{2}) (x - α^{3}) g4(x)=(x−α0)(x−α1)(x−α2)(x−α3)
与 (x + ai) 相同,因为 GF(2^8)计算如下.
g4(x) = x ^{4} - (α^{3}+α^{2}+α^{1}+α^{0}) x3 + ((α^{0}+α^{1}) (α^{2}+α^{3})+(α^{5}+α^{1})) x2 + (α^{6}+α^{5}+α^{4}+α^{3}) x +α^{6}
g4(x) = x^{4} - (α^{3}+α^{2}+α^{1}+α^{0}) x3 + (α^{2}+α^{3}+α^{3}+α^{4}+α^{5}+α^{1}) x2 + (α^{6}+α^{5}+α^{4}+α^{3}) x +α^{6}
g4(x) = x^{4} - (α^{3}+α^{2}+α^{1}+α^{0}) x3 + (α^{5}+α^{4}+α^{2}+α^{1}) x2 + (α^{6+α^{5+α^{4+α^{3) x +α^{6}
g4(x) = 01 x^{4} + 0f x^{3} + 36 x^{2} + 78 x + 40
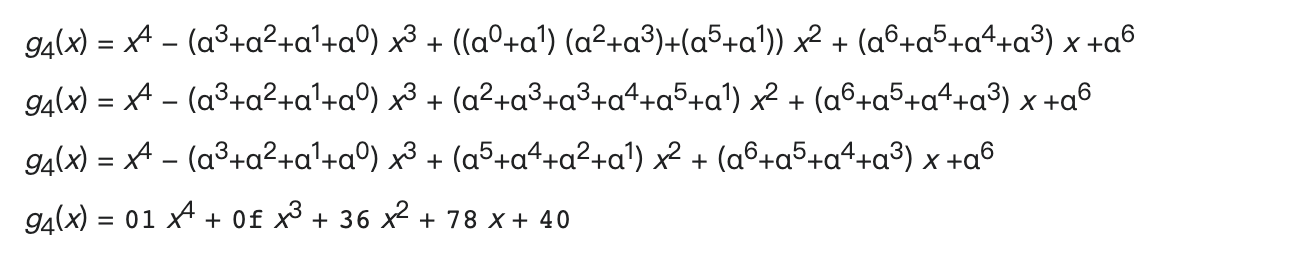
这是一个计算给定数量的纠错符号的生成多项式的函数。
def rs_generator_poly(nsym):
'''Generate an irreducible generator polynomial (necessary to encode a message into Reed-Solomon)'''
g = [1]
for i in range(0, nsym):
g = gf_poly_mul(g, [1, gf_pow(2, i)])
return g
这个函数有些低效,因为它为g分配了连续变大的数组。虽然这在实践中不太可能成为性能问题,但是喜欢优化的读者可能会觉得有趣,将其重新编写为只分配一次g的函数,或者可以计算一次并记忆g,因为g对于给定的nsym是固定的,所以可以重用g。
5.2.4 多项式除法
多种多项式除法算法存在,最简单的算法通常在小学就会教授,叫做长除法。下面的例子展示了对消息12 34 56进行除法运算的计算过程。
12 da df
-------------------------------------
01 0f 36 78 40 ) 12 34 56 00 00 00 00
^ 12 ee 2b 23 f4
----------------
da 7d 23 f4 00
^ da a2 85 79 84
----------------
df a6 8d 84 00
^ df 91 6b fc d9
----------------
37 e6 78 d9
注:多项式长除法的概念适用于这里,但有一些重要的区别:在计算从除数中减去的结果项/系数时,执行的是位无进位乘法,将结果“比特串”从第一个遇到的 MSB 开始与所选择的本原多项式进行异或操作,直到答案小于有限域的值,即这里的 256。然后像通常一样执行 XOR “减法”。
为了说明一个操作的方法(0x12 * 0x36):
00010010 ( 12 )
x 00110110 ( 36 )
00110110
00110110
001100001100
^100011101 <-- XOR with primitive polynomial value (11D)...
000100110110
^100011101 <-- ...until answer is less than 256.
00101011
2 b
这个余数和原始消息拼接在一起,因此编码后的消息为 12 34 56 37 e6 78 d9。
然而,长除法非常慢,因为它需要许多递归迭代才能终止。可以设计更有效的策略,例如使用合成除法(也称为霍纳法,Khan Academy 上有一个好的教程视频)。下面是一个实现了 GF(2^p) 多项式的扩展合成除法的函数(扩展是因为除数是多项式而不是单项式):
def gf_poly_div(dividend, divisor):
'''Fast polynomial division by using Extended Synthetic Division and optimized for GF(2^p) computations
(doesn't work with standard polynomials outside of this galois field, see the Wikipedia article for generic algorithm).'''
# CAUTION: this function expects polynomials to follow the opposite convention at decoding:
# the terms must go from the biggest to lowest degree (while most other functions here expect
# a list from lowest to biggest degree). eg: 1 + 2x + 5x^2 = [5, 2, 1], NOT [1, 2, 5]
msg_out = list(dividend) # Copy the dividend
#normalizer = divisor[0] # precomputing for performance
for i in range(0, len(dividend) - (len(divisor)-1)):
#msg_out[i] /= normalizer # for general polynomial division (when polynomials are non-monic), the usual way of using
# synthetic division is to divide the divisor g(x) with its leading coefficient, but not needed here.
coef = msg_out[i] # precaching
if coef != 0: # log(0) is undefined, so we need to avoid that case explicitly (and it's also a good optimization).
for j in range(1, len(divisor)): # in synthetic division, we always skip the first coefficient of the divisior,
# because it's only used to normalize the dividend coefficient
if divisor[j] != 0: # log(0) is undefined
msg_out[i + j] ^= gf_mul(divisor[j], coef) # equivalent to the more mathematically correct
# (but xoring directly is faster): msg_out[i + j] += -divisor[j] * coef
# The resulting msg_out contains both the quotient and the remainder, the remainder being the size of the divisor
# (the remainder has necessarily the same degree as the divisor -- not length but degree == length-1 -- since it's
# what we couldn't divide from the dividend), so we compute the index where this separation is, and return the quotient and remainder.
separator = -(len(divisor)-1)
return msg_out[:separator], msg_out[separator:] # return quotient, remainder.
5.2.5 编码主要函数
现在,以下是如何对消息进行编码以获取其 RS 代码:
def rs_encode_msg(msg_in, nsym):
'''Reed-Solomon main encoding function'''
gen = rs_generator_poly(nsym)
# Pad the message, then divide it by the irreducible generator polynomial
_, remainder = gf_poly_div(msg_in + [0] * (len(gen)-1), gen)
# The remainder is our RS code! Just append it to our original message to get our full codeword (this represents a polynomial of max 256 terms)
msg_out = msg_in + remainder
# Return the codeword
return msg_out
简单易懂吧?实际上,编码是Reed-Solomon中最简单的部分,它总是采用相同的方法(多项式除法)。译码是Reed-Solomon中最困难的部分,你会发现根据你的需要有很多不同的算法,但我们稍后会涉及这个问题。
这个函数非常快,但由于编码非常关键,这里提供一个增强的编码函数,它内联了多项式合成除法,这是你在Reed-Solomon软件库中最常见的形式。
def rs_encode_msg(msg_in, nsym):
'''Reed-Solomon main encoding function, using polynomial division (algorithm Extended Synthetic Division)'''
if (len(msg_in) + nsym) > 255: raise ValueError("Message is too long (%i when max is 255)" % (len(msg_in)+nsym))
gen = rs_generator_poly(nsym)
# Init msg_out with the values inside msg_in and pad with len(gen)-1 bytes (which is the number of ecc symbols).
msg_out = [0] * (len(msg_in) + len(gen)-1)
# Initializing the Synthetic Division with the dividend (= input message polynomial)
msg_out[:len(msg_in)] = msg_in
# Synthetic division main loop
for i in range(len(msg_in)):
# Note that it's msg_out here, not msg_in. Thus, we reuse the updated value at each iteration
# (this is how Synthetic Division works: instead of storing in a temporary register the intermediate values,
# we directly commit them to the output).
coef = msg_out[i]
# log(0) is undefined, so we need to manually check for this case. There's no need to check
# the divisor here because we know it can't be 0 since we generated it.
if coef != 0:
# in synthetic division, we always skip the first coefficient of the divisior, because it's only used to normalize the dividend coefficient (which is here useless since the divisor, the generator polynomial, is always monic)
for j in range(1, len(gen)):
msg_out[i+j] ^= gf_mul(gen[j], coef) # equivalent to msg_out[i+j] += gf_mul(gen[j], coef)
# At this point, the Extended Synthetic Divison is done, msg_out contains the quotient in msg_out[:len(msg_in)]
# and the remainder in msg_out[len(msg_in):]. Here for RS encoding, we don't need the quotient but only the remainder
# (which represents the RS code), so we can just overwrite the quotient with the input message, so that we get
# our complete codeword composed of the message + code.
msg_out[:len(msg_in)] = msg_in
return msg_out
该算法速度较快,但在实际使用中仍然相当慢,特别是在Python中。可以使用各种技巧来优化速度,例如内联(不使用gf_mul,而是避免调用操作),通过预计算(gen和coef的对数,甚至是生成乘法表),使用静态类型结构(将gf_log和gf_exp分配给array.array(‘i’,[…])),使用内存视图(例如将所有列表更改为bytearray),使用PyPy运行,或将算法转换为Cython或C扩展[1]。
此示例显示将编码函数应用于先前介绍的示例QR码中的消息。计算出的纠错符号(第二行)与从QR码解码的值相匹配。
>>> msg_in = [ 0x40, 0xd2, 0x75, 0x47, 0x76, 0x17, 0x32, 0x06,
... 0x27, 0x26, 0x96, 0xc6, 0xc6, 0x96, 0x70, 0xec ]
>>> msg = rs_encode_msg(msg_in, 10)
>>> for i in range(0,len(msg)):
... print(hex(msg[i]), end=' ')
...
0x40 0xd2 0x75 0x47 0x76 0x17 0x32 0x6 0x27 0x26 0x96 0xc6 0xc6 0x96 0x70 0xec
0xbc 0x2a 0x90 0x13 0x6b 0xaf 0xef 0xfd 0x4b 0xe0
Python版本说明:print函数的语法已经发生变化,此示例使用Python 3.0+版本。在以前的Python版本中(特别是Python 2.x),将print行替换为print hex(msg[i]),(包括逗号)和range替换为xrange。
5.3 RS 解码
5.3.1 解码大纲
里德-所罗门解码是一个从可能已损坏的消息和RS码中返回纠正后的消息的过程。换句话说,解码是使用先前计算的RS码修复消息的过程。
尽管只有一种方法可以使用里德-所罗门对消息进行编码,但是有很多不同的方法可以对它们进行解码,因此有很多不同的解码算法。
然而,我们通常可以用5个步骤概述解码过程[2][3]:
- 计算综合多项式。这使我们能够使用Berlekamp-Massey(或其他算法)分析错误的字符,并快速检查输入消息是否被破坏。
- 计算擦除/错误定位多项式(从综合多项式)。这是由Berlekamp-Massey计算的,并且是一个检测器,将准确告诉我们哪些字符被破坏。
- 计算擦除/错误评估多项式(从综合多项式和擦除/错误定位多项式)。评估字符被篡改的程度所必需的(即,有助于计算幅度)。
- 计算擦除/错误幅度多项式(从上述所有3个多项式):这个多项式也可以称为腐败多项式,因为事实上它确切地存储了需要从接收到的消息中减去的值以获得原始的,正确的消息(即,具有擦除字符的正确值)。换句话说,在这一点上,我们从这个多项式中提取了噪声,并且只需从输入消息中去除这个噪声即可修复它。
- 通过从输入消息中减去幅度多项式来修复输入消息。
我们将在下面描述这五个步骤。
此外,解码器还可以按照它们可以修复的错误类型进行分类:擦除(我们知道损坏字符的位置但不知道幅度),错误(我们忽略位置和幅度),或者错误和擦除的混合。我们将介绍如何支持所有这些。
5.3.2 综合征计算
解码里德-所罗门消息涉及几个步骤。第一步是计算消息的"综合征"。将消息视为一个多项式,并在α0、α1、α2、…、αn处对其进行求值。由于这些是生成多项式的零点,如果扫描到的消息没有损坏,结果应该是零(这可以用来检查消息是否损坏,以及在修复损坏的消息后,如果消息完全修复)。如果不是,综合征包含了确定应该进行的校正所需的所有信息。编写一个函数来计算综合征很简单:
def rs_calc_syndromes(msg, nsym):
'''给定接收到的码字msg和纠错符号的数量(nsym),计算综合征多项式。
从数学上讲,它本质上等同于傅里叶变换(Chien搜索是其逆变换)。
# 注意 "[0] + ":我们为最低次(常数)添加一个0系数。这实际上会移动综合征,并且会移动所有依赖于综合征的计算(例如错误定位多项式、错误评估多项式等,但不包括错误位置)。
# 这不是必需的,你可以调整后续计算从0开始而不是跳过第一次迭代(即,通常看到的范围(1,n-k+1)),
synd = [0] * nsym
for i in range(0, nsym):
synd[i] = gf_poly_eval(msg, gf_pow(2,i))
return [0] + synd # 用一个0填充以获得数学精度(否则我们有时可能会得到奇怪的计算)
继续示例,我们发现原始码字在没有任何损坏的情况下的综合征确实为零。在消息或其RS码中至少引入一个字符的损坏会导致非零的综合征。
===>synd = rs_calc_syndromes(msg, 10)
===>print(synd)
===>[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # 没有损坏的消息 = 全部为0的综合征
===>msg[0] = 0 # 故意损坏消息
===>synd = rs_calc_syndromes(msg, 10)
===>print(synd)
===>[0, 64, 192, 93, 231, 52, 92, 228, 49, 83, 245] # 当损坏时,综合征将为非零
下面是自动化检查的代码:
def rs_check(msg, nsym):
'''如果 message + ecc 没有错误则返回 true 否则返回 false(可能并不总是捕获错误的解码或错误的消息,特别是如果有太多错误 - 在 Singleton 界限之上 - 但它通常会)'''
return ( max(rs_calc_syndromes(msg, nsym)) == 0 )
5.3.3 擦除校正
如果已知错误的位置,纠正代码中的错误是最简单的。这被称为擦除纠正。对于添加到代码中的每个纠错符号,可以纠正一个擦除的符号(即字符)。如果未知错误位置,则每个符号错误需要两个EC符号(因此您可以纠正的错误数量是擦除数量的两倍少)。如果正在扫描的QR码的一部分被遮盖或物理撕掉,那么擦除纠正在实践中是有用的。然而,对于扫描仪来说,确定这种情况发生可能会很困难,因此并非所有的QR码扫描仪都能执行擦除纠正。
现在我们已经有了综合征,我们需要计算定位多项式。这很简单:
def rs_find_errata_locator(e_pos):
'''从擦除/错误/错位的位置计算擦除/错误/错位定位多项式(位置必须相对于x系数,例如:"hello worldxxxxxxxxx"被篡改为"h_ll_ worldxxxxxxxxx",其中xxxxxxxxx是长度为n-k=9的ecc,这里的字符串位置是[1, 4],但系数是相反的,因为ecc字符被放置为多项式的第一个系数,因此擦除字符的系数是n-1 - [1, 4] = [18, 15] = erasures_loc,将其指定为参数。'''
e_loc = [1] # 只是为了初始化,因为我们要乘法,所以它必须是 1,这样乘法才能正确开始,而不会使任何项为零 .
for i in e_pos:
e_loc = gf_poly_mul( e_loc, gf_poly_add([1], [gf_pow(2, i), 0]) )
return e_loc
接下来,从定位多项式计算擦除/错误估算多项式很容易,只需进行一次多项式乘法,然后进行一次多项式除法(您可以将其替换为列表切片,因为最终我们想要的是这种效果):
def rs_find_error_evaluator(synd, err_loc, nsym):
'''根据综合和错误/擦除/误差定位多项式Sigma,计算错误(或擦除,如果提供了sigma=擦除定位多项式或误差)估算多项式Omega。'''
# Omega(x) = [ Synd(x) * Error_loc(x) ] mod x^(n-k+1)
_, remainder = gf_poly_div( gf_poly_mul(synd, err_loc), ([1] + [0]*(nsym+1)) ) # 首先将综合和错误定位多项式相乘,然后执行多项式除法以将多项式截断到所需长度。
#下面提供了更快的等价方法。
# 首先,将综合与错误定位多项式相乘。然后,使用切片操作截断多项式(即列表),将其截断为所需长度。这等价于使用长度为所需长度的多项式进行除法。
return remainder
该函数名为rs_find_error_evaluator,它接受三个参数synd、err_loc和nsym,并计算出错误(或擦除,如果您提供sigma=擦除定位多项式,或误差)估算多项式Omega,从综合和错误/擦除/误差定位Sigma中获取。
在函数中,使用公式Omega(x)=[ Synd(x) * Error_loc(x) ] mod
x^(n-k+1)来计算估算多项式。首先,使用gf_poly_mul函数计算出综合和错误定位多项式的乘积,然后使用gf_poly_div函数执行多项式除法,以截断多项式到所需长度。将商作为函数返回值。注释中还提供了更快速的实现方式,但等价于原来的实现方式。
最后,使用Forney算法计算校正值(也称为错误幅度多项式)。它在以下函数中实现。
def rs_correct_errata(msg_in, synd, err_pos): # err_pos is a list of the positions of the errors/erasures/errata
'''Forney算法计算校正值(即错误幅度),以纠正输入消息中的错误。'''
# 计算误差定位多项式以同时纠正错误和擦除(将BM算法得到的错误位置与调用者提供的擦除位置相结合)。
coef_pos = [len(msg_in) - 1 - p for p in err_pos] #为使误差定位算法工作,需要将位置转换为系数的次数(例如:将 [0, 1, 2] 转换为 [len(msg)-1, len(msg)-2, len(msg) -3])。
err_loc = rs_find_errata_locator(coef_pos)
# 计算误差估算多项式(在学术论文中通常称为Omega或Gamma)。
err_eval = rs_find_error_evaluator(synd[::-1], err_loc, len(err_loc)-1)[::-1]
# Chien搜索的第二部分是根据错误定位多项式的根(即,它的值为0的位置)中的错误位置,获取错误定位多项式X。
X = [] # 存储错误的位置
for i in range(0, len(coef_pos)):
l = 255 - coef_pos[i]
X.append( gf_pow(2, -l) )
# Forney 算法:计算幅度
E = [0] * (len(msg_in)) # w将需要更正(减去)的值存储到包含错误的消息中。 这有时称为误差幅度多项式。
Xlength = len(X)
for i, Xi in enumerate(X):
Xi_inv = gf_inverse(Xi)
# 计算错误定位多项式的形式导数(详见Blahut的《数据传输的代数码》第196-197页)。误差定位多项式的形式导数用作Forney算法的分母,该算法简单地表示第i个错误值由error_evaluator(gf_inverse(Xi)) / error_locator_derivative(gf_inverse(Xi))给出。详见Blahut的《数据传输的代数码》第196-197页。
err_loc_prime_tmp = []
for j in range(0, Xlength):
if j != i:
err_loc_prime_tmp.append( gf_sub(1, gf_mul(Xi_inv, X[j])) )
#计算乘积,它是 Forney 算法的分母(勘误表定位器导数)
err_loc_prime = 1
for coef in err_loc_prime_tmp:
err_loc_prime = gf_mul(err_loc_prime, coef)
'''
等价于:err_loc_prime = functools.reduce(gf_mul, err_loc_prime_tmp, 1)
计算y(误差估算多项式的评估值)。
这是对理论方程的更忠实的翻译,与旧版的Forney方法相反。在这里,它是一个完全的再现:
对于X中的每个元素j,计算Yl = omega(Xl.inverse()) / prod(1 - Xj*Xl.inverse()),其中prod表示所有j的乘积。
'''
y = gf_poly_eval(err_eval[::-1], Xi_inv) #Forney 算法的分子(勘误表评估)
y = gf_mul(gf_pow(Xi, 1), y)
# Check: err_loc_prime (the divisor) should not be zero.
if err_loc_prime == 0:
raise ReedSolomonError("Could not find error magnitude") # 找不到误差大小
#计算幅度
magnitude = gf_div(y, err_loc_prime) # 由Forney算法计算得出的错误的幅度值,实际上是一个方程式:将误差估算多项式除以误差定位多项式的导数,即可得到误差幅度(即需要修复的值),其为第i个符号的值。
E[err_pos[i]] = magnitude # 将这个错误的幅度值存储到幅度多项式中。
#应用校正值以获得纠正后的消息!(请注意,纠正后的ECC字节也会得到纠正!)
msg_in = gf_poly_add(msg_in, E) #等价于Ci = Ri - Ei,其中Ci是正确的消息,Ri是接收的(感知)消息,Ei是误差幅度(减号被XOR替换,因为在GF(2^p)中它是等价的)。因此,实际上我们从接收到的消息中减去了错误的幅度值,逻辑上将值更正为它应该是的值。
return msg_in
数学注释:误差值表达式的分母是误差定位多项式q的形式导数。这可以通过通常的过程将每个cnxn项替换为ncn xn-1来计算。由于我们在特征为2的域中工作,当n为奇数时,ncn等于cn,当n为偶数时等于0。因此,我们可以简单地删除偶数系数(得到多项式qprime),并评估qprime(x2)。
Python注释:该函数使用[::-1]来反转列表中元素的顺序。这是必要的,因为函数不都使用相同的排序约定(即,有些使用最小项首先,而其他函数使用最大项首先)。它还使用了列表推导式,这只是一种简洁的写法,用于在列表中追加项目的for循环,但Python解释器可以比循环更加优化。
继续上面的例子,这里我们使用rs_correct_errata来恢复消息的第一个字节。
>>> msg[0] = 0
>>> synd = rs_calc_syndromes(msg, 10)
>>> msg = rs_correct_errata(msg, synd, [0]) #[0] 是擦除位置的列表,这里是第一个字符,在位置 0
>>> print(hex(msg[0]))
0x40
5.3.4 纠错
在错误位置未知的情况下(通常我们称之为错误,与已知位置的擦除相对),我们将使用与擦除相同的步骤,但现在需要额外的步骤来找到位置。使用Berlekamp-Massey算法计算错误定位多项式,稍后我们可以使用它来确定错误位置:
def rs_find_error_locator(synd, nsym, erase_loc=None, erase_count=0):
'''使用 Berlekamp-Massey 算法查找错误/勘误表定位器和评估器多项式'''
# BM 将迭代地估计错误定位器多项式。
# 为此,它将计算一个名为 Delta 的差异项,它将告诉我们错误定位器多项式是否需要更新
#(因此称为差异的原因:它告诉我们何时偏离正确值) .
# 初始化多项式
if erase_loc: # 如果提供了擦除定位器多项式,我们用它的值初始化,这样我们就可以在最终的定位器多项式中包含擦除
err_loc = list(erase_loc)
old_loc = list(erase_loc)
else:
err_loc = [1] # 这是我们要填充的主要变量,在其他符号中也称为 Sigma 或更正式的错误/勘误定位器多项式。
old_loc = [1] BM 是一种迭代算法,我们需要上一次迭代的勘误定位器多项式,以便更新其他必要的变量。
#L = 0 # 更新标志变量,这里不需要,因为我们使用另一种等效方法来检查是否需要更新(但使用标志可能会更快,具体取决于使用长度(列表)是否在您的语言中花费线性时间,在 Python 中,它是常量,所以速度一样快。
# 修复综合征转移:在计算综合征时,某些实现可能会为最低阶项(常量)添加一个 0 系数。这是综合症转移的情况,因此综合症将大于 ecc 符号的数量(我不知道这种转移的目的是什么)。如果是这种情况,那么当我们使用诸如 BM 内部的综合症时,我们需要通过跳过那些前置系数来考虑综合症转移。
# 检测移位的另一种方法是检测 0 系数:根据定义,校正子不包含任何 0 系数(除非没有错误/擦除,在这种情况下它们都是 0)。然而,这不适用于修改后的 Forney 综合征,它将与擦除对应的系数设置为 0,
synd_shift = len(synd) - nsym
for i in range(0, nsym-erase_count):
for i in range ( 0 , nsym - erase_count ): # 通常:nsym-erase_count == len(synd),除非你输入部分 erase_loc 并使用完整综合症而不是 Forney 综合症,在这种情况下 nsym-erase_count 是更正确(len(synd) 将因 IndexError 而严重失败)。
if erase_loc: # 如果提供了擦除定位器多项式来初始化错误定位器多项式,那么我们必须跳过第一个 erase_count 迭代(不是最后一个迭代,这非常重要!)
K = erase_count+i+synd_shift
else: # i如果没有提供擦除定位器,那么要么没有擦除,要么我们使用 Forney 综合症,所以我们不需要使用 erase_count 或 erase_loc(擦除已从 Forney 综合症中删除)。
K = i+synd_shift
# 计算差异 Delta
# 这是计算差异 Delta 的接近账面操作:它是错误定位器与综合症的简单多项式乘法,然后我们得到第 K 个元素。
#delta = gf_poly_mul(err_loc[::-1], synd)[K] # 理论上应该是 gf_poly_add(synd[::-1], [1])[::-1] 而不仅仅是 synd,但它似乎没有必要正确解码。
# 但这可以优化:因为我们只需要第 K 个元素,所以除了第 K 个元素之外,我们不需要计算任何其他元素的多项式乘法。因此为了优化,我们只在我们需要的项目上计算 polymul,跳过其余部分(避免嵌套循环,因此我们是线性时间而不是二次)。
# 这种优化实际上在《Algebraic codes for data transmission》一书的几个图中都有描述,Blahut, Richard E., 2003, Cambridge university press。
delta = synd[K]
for j in range(1, len(err_loc)):
delta ^= gf_mul(err_loc[-(j+1)], synd[K - j]) # 增量也称为差异。这里我们进行部分多项式乘法(即,我们只计算 K 次多项式的多项式乘法)。应该等同于 brownanrs.polynomial.mul_at()。
#print "delta", K, delta, list(gf_poly_mul(err_loc[::-1], synd)) # 调试线
# 移动多项式来计算下一个度数
old_loc = old_loc + [0]
# Iteratively estimate the errata locator and evaluator polynomials
if delta != 0: # # 仅当存在差异时更新
if len(old_loc) > len(err_loc): # 规则 B(规则 A 是隐式定义的,因为规则 A 只是说我们跳过此迭代的任何修改)
#if 2*L <= K+erase_count: # 等同于 len(old_loc) > len(err_loc),只要正确计算 L
# 计算勘误定位器多项式 Sigma
new_loc = gf_poly_scale(old_loc, delta)
old_loc = gf_poly_scale(err_loc, gf_inverse(delta)) # 实际上我们在做 err_loc * 1/delta = err_loc // delta
err_loc = new_loc
# 更新更新标志
#L = K - L # 更新标志 L 是棘手的:在 Blahut 的模式中,必须使用 `L = K - L - erase_count`(实际上在这个函数的前一个草稿中,如果你忘记做 `- erase_count ` 它会导致仅更正 2*(errors+erasures) <= (nk) 而不是 2*errors+erasures <= (nk)),但在最新的草案中,这会在某些情况下导致错误解码它应该正确解码!因此,您应该尝试使用和不使用 `-erase_count` 在您自己的实现中更新 L 并查看哪个工作正常而不会产生错误的解码失败。
# 更新差异
err_loc = gf_poly_add(err_loc, gf_poly_scale(old_loc, delta))
# 检查结果是否正确,没有太多错误需要更正
while len(err_loc) and err_loc[0] == 0: del err_loc[0] #删除前导 0,否则错误的大小不正确
errs = len ( err_loc ) - 1
if (errs-erase_count) * 2 + erase_count > nsym:
raise ReedSolomonError("Too many errors to correct") # 太多错误无法纠正
return err_loc
对于给定的syndromes和擦除的位置信息,使用Berlekamp-Massey算法找到错误/擦除位置定位器和估算器多项式。算法通过迭代估计错误位置定位器多项式,计算一个称为Delta的差异项,该项告诉我们错误定位器多项式是否需要更新。如果有擦除位置信息,将使用擦除位置定位器多项式来初始化错误定位器多项式,以便在最终定位器多项式中包含擦除。
然后,使用误差定位多项式,我们简单地使用一种称为试验代入的暴力方法来查找此多项式的零点,以确定错误位置(即需要更正的字符的索引)。还存在一种更高效的算法称为Chien搜索,它避免了在每个迭代步骤中重新计算整个评估过程,但是此算法留给读者作为练习。
def rs_find_errors(err_loc, nmess): # nmess is len(msg_in)
'''通过暴力试位法(trial substitution),找到错误多项式的根(即,使得多项式的值等于零的位置),这是一种类似于Chien搜索的方法(但不如Chien搜索高效,Chien搜索是一种仅需常数时间的多项式求值算法)。'''
errs = len(err_loc) - 1
err_pos = []
for i in range(nmess): # 通常我们应该尝试所有 2^8 个可能的值,但在这里我们优化为只检查有趣的符号
if gf_poly_eval(err_loc, gf_pow(2, i)) == 0: # 这是一个0吗?那就是错误定位多项式的一个根,换句话说,就是一个错误的位置。
err_pos.append(nmess - 1 - i)
# 完整性检查:发现的错误/勘误位置的数量应与勘误定位器多项式的长度完全相同
if len(err_pos) != errs:
# c找不到错误位置
raise ReedSolomonError("Too many (or few) errors found by Chien Search for the errata locator polynomial!")
return err_pos
这里介绍一个数学知识:当错误定位多项式是线性的(err_poly长度为2)时,可以很容易地解决,而不必使用试错方法。上面介绍的函数没有利用这一事实,但有兴趣的读者可能希望实现更有效的解决方案。同样地,当错误定位是二次的时,可以通过使用二次公式的一般化来解决。更有雄心壮志的读者可能希望也实现这个过程。
下面是一个示例,其中纠正了消息中的三个错误:
>>> print(hex(msg[10]))
0x96
>>> msg[0] = 6
>>> msg[10] = 7
>>> msg[20] = 8
>>> synd = rs_calc_syndromes(msg, 10)
>>> err_loc = rs_find_error_locator(synd, nsym)
>>> pos = rs_find_errors(err_loc[::-1], len(msg)) # find the errors locations
>>> print(pos)
[20, 10, 0]
>>> msg = rs_correct_errata(msg, synd, pos)
>>> print(hex(msg[10]))
0x96
5.3.5 错误和擦除校正
Reed-Solomon 解码器可以同时解码差错和擦除,但其上限是有限制的,称为 Singleton Bound,即 2*e+v <= (n-k),其中 e 是错误数量,v 是擦除数量,(n-k) 是 RS 码字符数量(在代码中称为 nsym)。基本上,这意味着对于每个擦除,您只需要一个 RS 码字符进行修复,而对于每个错误,您需要两个 RS 码字符(因为您需要找到除值/幅度以外的位置)。这样的解码器称为错误和擦除解码器,或错误修正解码器。
为了同时纠正差错和擦除,我们必须防止擦除干扰差错定位过程。这可以通过计算 Forney Syndrome 来完成,如下所示。
def rs_forney_syndromes(synd, pos, nmess):
# “Compute Forney syndromes” 的翻译是计算 Forney 校验码,它计算的是一种修改过的校验码,仅计算错误(删除了已知的位置)。请不要将其与 Forney 算法混淆,后者基于错误的位置对消息进行纠正。
erase_pos_reversed = [nmess-1-p for p in pos] #准备系数度位置(而不是擦除位置)
# 优化方法,所有操作都是内联的
fsynd = list(synd[1:]) # 复制并修剪第一个系数,根据定义始终为 0
for i in range(0, len(pos)):
x = gf_pow(2, erase_pos_reversed[i])
for j in range(0, len(fsynd) - 1):
fsynd[j] = gf_mul(fsynd[j], x) ^ fsynd[j + 1]
# 一个等价、理论上的计算修改后的Forney syndromes的方法是:fsynd = (erase_loc * synd) % x^(n-k)
# 这里的erase_loc是已知擦除位置的定位多项式,通过rs_find_errata_locator函数计算得到。synd是原始的syndrome多项式,长度为n-k+1。在上述等式中,先将erase_loc和synd相乘,然后对结果进行模运算,模数为x^(n-k),即保留结果的前n-k+1项系数。
# 这个等式的推导参考了Shao等人在1986年发表的文章《A single chip VLSI Reed-Solomon decoder》中的内容。在计算出修改后的Forney syndromes之后,接下来可以应用Berlekamp-Massey算法来计算出错误定位多项式。
return fsynd
接下来可以使用Forney syndromes代替常规的syndromes进行误差定位过程。
rs_correct_msg函数将整个过程结合起来。通过提供erase_pos,即在消息msg_in中指定的擦除索引位置列表(完整的接收消息:原始消息+ecc)来表示擦除。
def rs_correct_msg(msg_in, nsym, erase_pos=None):
'''Reed-Solomon 主要解码函数'''
if len(msg_in) > 255: # 无法解码,消息太大
raise ValueError("Message is too long (%i when max is 255)" % len(msg_in))
msg_out = list(msg_in) # 复制这个消息
# 擦除:将它们设置为空字节以便更容易解码(但这不是必需的,它们无论如何都会被更正,但是使用空字节进行调试会更容易,因为错误定位多项式的值只取决于错误位置,而不是它们的值)
if erase_pos is None:
erase_pos = []
else:
for e_pos in erase_pos:
msg_out[e_pos] = 0
# 检查是否有太多擦除需要更正(超出单例范围)
if len(erase_pos) > nsym: raise ReedSolomonError("Too many erasures to correct")
# 仅使用错误准备综合多项式(即:错误 = 被空字节替换的字符
# 或更改为另一个字符,但我们不知道他们的位置)
synd = rs_calc_syndromes(msg_out, nsym)
# 检查输入码字中是否有任何错误/擦除。如果没有(所有校验码系数为0),则直接返回原始消息。
if max(synd) == 0:
return msg_out[:-nsym], msg_out[-nsym:] # no errors
# 计算 Forney 综合症,它隐藏了原始综合症的擦除(这样 BM 只需要处理错误,而不是擦除)
fsynd = rs_forney_syndromes(synd, erase_pos, len(msg_out))
# compute the error locator polynomial using Berlekamp-Massey
err_loc = rs_find_error_locator(fsynd, nsym, erase_count=len(erase_pos))
# locate the message errors using Chien search (or brute-force search)
err_pos = rs_find_errors(err_loc[::-1] , len(msg_out))
if err_pos is None:
raise ReedSolomonError("Could not locate error") # error location failed
# 查找错误值并应用它们来更正消息计算勘误评估器和勘误幅度多项式,然后更正错误和擦除
msg_out = rs_correct_errata(msg_out, synd, (erase_pos + err_pos)) # 请注意,我们这里使用的是原始综合症,而不是福尼综合症
# (因为我们会同时纠正错误和删除,所以我们需要完整的综合症)
# 检查最终消息是否已完全修复
synd = rs_calc_syndromes(msg_out, nsym)
if max(synd) > 0:
raise ReedSolomonError("Could not correct message") # 无法修复消息
# 返回解码成功的信息
return msg_out[:-nsym], msg_out[-nsym:] #还返回更正后的 ecc 块,以便用户可以检查()
Python注意事项:列表erase_pos和err_pos使用+运算符连接。
这是一个完全操作的错误和抹除纠正Reed-Solomon解码器所需的最后一块。如果您想更深入地了解勘误(错误和抹除)解码器的内部工作原理,可以阅读理查德·E·布拉胡特(Richard E. Blahut)于2003年出版的优秀著作“数据传输的代数编码”。
数学注释:在某些软件实现中,特别是使用针对线性代数和矩阵操作优化的语言的实现中,算法(编码,Berlekamp-Massey等)似乎完全不同,使用傅里叶变换。这是因为它是完全等效的:当用频谱估计术语陈述时,解码Reed-Solomon由傅里叶变换(综合器计算器)组成,随后是频谱分析(Berlekamp-Massey或欧几里得算法),然后是逆傅里叶变换(Chien搜索)。有关更多信息,请参见Blahut图书[4]。实际上,如果您使用针对线性代数进行了优化的编程语言,或者想要使用快速的线性代数库,则使用傅里叶变换可能是一个非常好的主意,因为现在它非常快(特别是快速傅里叶变换或数论变换[5])。
6.以一个例子结束
下面是一个示例,说明如何使用您刚刚创建的函数,以及如何解码错误和擦除:
# Configuration of the parameters and input message
prim = 0x11d
n = 20 # set the size you want, it must be > k, the remaining n-k symbols will be the ECC code (more is better)
k = 11 # k = len(message)
message = "hello world" # input message
# Initializing the log/antilog tables
init_tables(prim)
# Encoding the input message
mesecc = rs_encode_msg([ord(x) for x in message], n-k)
print("Original: %s" % mesecc)
# Tampering 6 characters of the message (over 9 ecc symbols, so we are above the Singleton Bound)
mesecc[0] = 0
mesecc[1] = 2
mesecc[2] = 2
mesecc[3] = 2
mesecc[4] = 2
mesecc[5] = 2
print("Corrupted: %s" % mesecc)
# Decoding/repairing the corrupted message, by providing the locations of a few erasures, we get below the Singleton Bound
# Remember that the Singleton Bound is: 2*e+v <= (n-k)
corrected_message, corrected_ecc = rs_correct_msg(mesecc, n-k, erase_pos=[0, 1, 2])
print("Repaired: %s" % (corrected_message+corrected_ecc))
print(''.join([chr(x) for x in corrected_message]))
输出如下:
Original: [104, 101, 108, 108, 111, 32, 119, 111, 114, 108, 100, 145, 124, 96, 105, 94, 31, 179, 149, 163]
Corrupted: [ 0, 2, 2, 2, 2, 2, 119, 111, 114, 108, 100, 145, 124, 96, 105, 94, 31, 179, 149, 163]
Repaired: [104, 101, 108, 108, 111, 32, 119, 111, 114, 108, 100, 145, 124, 96, 105, 94, 31, 179, 149, 163]
hello world
7. 结论和进一步发展
本文介绍了Reed-Solomon码的基本原理,并提供了用于纠正读取错误的通用Reed-Solomon编解码器生成的QR码的Python代码。这里提供的代码相当通用,可以用于除QR码之外的任何需要纠正错误/擦除的用途,例如文件保护、网络等。由于编码理论是一个非常丰富的领域,因此许多这些思想的变化和改进是可能的。
如果你的代码只是针对自己的数据(例如,你想能够生成和读取自己的QR码),那么你就可以了,但如果你打算使用其他人提供的数据(例如,你想读取和解码其他应用程序的QR码),那么这个解码器可能不够用,因为为了简单起见,这里有一些隐藏的参数被固定了(即:生成器/阿尔法数字和第一个连续根)。如果你想解码其他库生成的Reed-Solomon码,你将需要使用通用的Reed-Solomon编解码器,这将允许你指定自己的参数,甚至超越 2 8 2^8 28域。
在补充资源页面上,你将找到一个扩展的、通用的代码版本,你可以用它来解码几乎任何Reed-Solomon码,还有一个生成素多项式列表的函数和一个检测未知RS码参数的算法。请注意,无论你使用什么参数,修复能力总是相同的:对于对数/反对数表和生成多项式的生成值不会改变Reed-Solomon码的结构,因此你总是会得到相同的功能,无论参数如何。事实上,修改任何可用参数都不会改变理论上定义的Singleton界限,这个界限定义了Reed-Solomon(以及理论上任何纠错码)的最大修复能力。
你可能已经注意到的一个直接的问题是,我们只能编码长度最多为256个字符的消息。这个限制可以通过几种方式来规避,其中最常见的三种是:
- 其中一种是使用更高的Galois域,例如 2 16 2^{16} 216,可以允许编码65536个字符,或$ 2 32 2^{32} 232、 2 64 2^{64} 264、 2 1 28 21^{28} 2128等。问题在于,对于大的多项式,编码和解码Reed-Solomon所需的多项式计算变得非常昂贵(大多数算法都是二次时间复杂度,最有效的算法是 n l o g n n log n nlogn,例如使用数论变换)。
- 另一种方法是将大数据流按256个字符的块进行编码。
- 还有一种方法是使用包大小包含的变体算法,例如Cauchy Reed-Solomon(见下文)。
如果你想更深入了解,有很多关于Reed-Solomon码的书籍和科学文章,一个好的起点是Richard Blahut,他在这个领域非常出色。此外,有很多不同的方式可以对Reed-Solomon码进行编码和解码,因此你会发现许多不同的算法,特别是用于解码的算法(Berlekamp-Massey,Berlekamp-Welch,欧几里得算法等)。
如果你正在寻找更好的性能,在文献中你会找到这里介绍的算法的几个变体,如Cauchy-Reed-Solomon。编程实现在你的Reed-Solomon编解码器的性能中也起着很大的作用,这可能会导致1000倍的速度差异。有关更多信息,请阅读附加资源的“优化性能”部分。
尽管现在近乎最优的前向纠错算法(如LDPC码、Turbo码等)因其极快的速度而受到热捧,但Reed-Solomon是一种最优的前向纠错码,这意味着它可以达到称为Singleton界限的理论极限。在实践中,这意味着RS可以同时纠正最多 2 ∗ e + v < = ( n − k ) 2*e+v <= (n-k) 2∗e+v<=(n−k)个错误和擦除,其中e是错误的数量,v是擦除的数量,k是消息大小,n是消息+码大小,(n-k)是最小距离。这并不是说近乎最优的前向纠错码是无用的:它们的速度比Reed-Solomon快得不可想象,而且它们可能不会受到悬崖效应的影响(这意味着即使存在太多错误以至于不能纠正所有错误,它们仍可能部分解码消息的某些部分,相反,RS将无疑失败,甚至会默默地解码错误的消息而没有任何检测),但它们肯定不能像Reed-Solomon那样纠正这么多的错误。在近乎最优和最优的前向纠错码之间选择主要是关注速度。
最近,由于发现了w:List_decoding(不要与软解码混淆),Reed-Solomon的研究领域重新获得了一些活力,这允许解码/修复比理论最优极限更多的符号。核心思想是,与标准Reed-Solomon只做唯一的解码(意味着它总是得出一个解决方案,如果它不能因为超过理论极限而返回错误或错误的结果,解码器将返回一个错误或错误的结果)不同,具有列表解码的Reed-Solomon仍会尝试超越极限并获得几种可能的结果,但通过对不同结果的巧妙检查,通常可以区分出可能是正确的多项式。
已经有一些列表解码算法可用,允许修复 n − s q r t ( n k ) n - sqrt(nk) n−sqrt(nk)[7]个符号,而不是 2 e + v < = ( n − k ) 2e+v <= (n-k) 2e+v<=(n−k),其他列表解码算法(更高效或解码更多的符号)目前正在研究中。
8. 第三方实现
如果您想查看实际示例,这里有一些 Reed–Solomon 的实现:
- Purely functional pure-Python Reedsolomon library Tomer Filiba 和 LRQ3000 的纯功能纯 Python Reedsolomon 库通过支持更多功能启发并扩展了本教程。
- Object-oriented Reed Solomon library in pure-PythonAndrew Brown 和 LRQ3000 编写的纯 Python 面向对象 Reed Solomon 库(与 userspace port here 的库具有相同的功能,但面向对象更接近于数学命名法)。
- Linux 内核中的 Reed-Solomon(这里有一个用户空间端口,最初是从 Phil Karn 的库libfec和libfec clone移植过来的)。
- ZXing (Zebra Crossing)一个用于生成和解码 QR 码的成熟库。
- Speed-optimized Reed-Solomon和 Cauchy-Reed-Solomon,带有大量评论和相关博客以获取更多详细信息(已不可用)。
- 另一个高速优化的Go 语言 Reed-Solomon。
- Port of code in the article rust语言实现。
- C++ Reed Solomon implementation该项目受这个教程的启发,使用堆栈内存分配和编译时可更改的
msg\ecc大小,专为嵌入式系统设计. - Interleaved Reed Solomon implementation in C++NinjaDevelper作者使用 C++ 实现的 Reed Solomon 实现。
- FastECC,C++ Reed Solomon 使用数论变换 (NTT) 在 $O(n log n) $中实现;该项目是开源的,采用 Apache License 2.0 许可证。声称在处理大数据时具有快速编码速率。
- Leopard-RS另一个用于快速处理大数据编码的 C++ 库,采用与 FastECC 稍有不同但类似的算法。
- Colin Davis 的Pure Go 实现(开源,GLPv3 许可)。
- Shorthair,该项目实现了UDP与纠错码相结合的方法,用于实现快速可靠的网络通信,以替代TCP协议栈或UDP复制技术(后者可以看作是一种低效的冗余方案)。该项目提供了幻灯片,详细描述了这种方法在实时游戏网络中的应用。
- Pure C Implementation 纯 C 实现使用 uint8_t 优化的纯 C 实现,非常高效。
- hqm rscode ANSI C 实现,用于 8 位符号;






















 7246
7246











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








