编译原理学习笔记之词法分析

最新推荐文章于 2024-09-25 01:08:49 发布

坚持奋斗的李洛克

最新推荐文章于 2024-09-25 01:08:49 发布

阅读量1.9k

点赞数 1

分类专栏：操作系统文章标签：编译原理

本文链接：https://blog.csdn.net/lz20120808/article/details/48677077

版权

操作系统专栏收录该内容

7 篇文章 1 订阅

订阅专栏

词法分析

词法分析是编译的第一个阶段，在单词的级别上分析和翻译源程序。

3.1正规文法和有限自动机

正规文法
– 是Chomsky 3型文法
正规文法是描述正规集（语言的集合）的文法，可用于描述程序设计语言的语法部分。
正规式
– 设A是非空的有限字母表，A={ai| i=1,2,……n},则
1. ε，Φ和ai (i=1,2,……n)都是正规式。
2. 若α、β是正规式，则α|β、 α•β 、α*、 β +也是正
规式。
3. 正规式只能通过有限次使用1，2规则获得一个正规语言可以用正规文法定义，也可以用正规式定义，对任意一个正规文法，存在一个定义同一个语言的正规式；同样，对每个正规式，存在一个生成同一语言的正规文法；有些正规语言很容易用文法定义，有些则用正规式定义更容易；两者之间是可以转换的，结构上具有等价性。
– 由正规文法或正规式定义的正规语言的集合构成正规集。

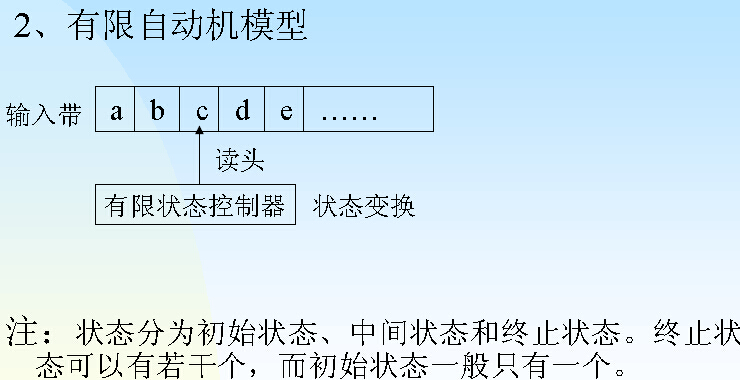
3.2有限自动机

•有限自动机是一种识别装置，它能准确地识别正规集。它为词法分析程序的构造提供了方法和工具。
•有限自动机是具有离散输入输出系统的数学模型。它具有有限数目的内部状态，系统可以根据当前所处的状态和面临的输入字符决定系统的后继行为。其当前状态概括了过去输入处理的信息。

这里写图片描述

一个状态加上一个输入只有一个结果就是一个确定自动机，否则就是不确定自动机。
3.2.1确定有限自动机DFA(Deterministic FA)
每读一个字符，状态就向前进至下一状态；记为：“┣”
–┣K表示自动机做了K步动作。
–┣*表示自动机做了0步动作或0步以上动作。
–┣+表示自动机做了1步动作或1步以上动作。

•(1)定义：确定有限自动机是一个五元式M(S,Σ,f,s0,Z）
–其中：S：有限状态集
–Σ：有限字母表
–f：S×Σ→S上的单值映射，f(s,a)=s’
–s0：唯一的初态，s0 ∈S
–Z：终止状态集，Z⊆S
•注：这里确定的含义，就是状态转换关系f是一个函数，即对于给定的当前状态s和当前读入的符号a，有唯一确定的下一状态s’。
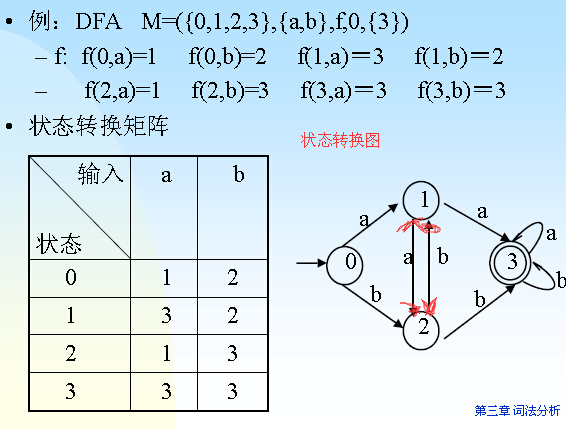
3.2.2状态转换关系表示：
–状态转换矩阵：DFA的映射关系由一个矩阵来表示。
–状态转换图：
注：1）用矩阵表示转换便于计算机处理，但不直观，而用状态转换图表示比较直观。
2）在整个状态转换图中只有一个初始状态结点，用“→”射入的结点表示初始状态。可有若干终止状态(也可能没有)，用双圆圈表示。若初始状态结点同时又是终止状态结点，则表示空串ε可为相应DFA识别。
这里写图片描述
3.2.3不确定有限自动机NFA(Non-deterministic FA)
(1)定义：不确定有限自动机是一个五元式
M=（S,Σ,f,S0,Z）
–其中：S：有限状态集
–Σ：有限字母表
–f：S×Σ→2S(S的子集)上的映射
–S0：非空的初态集，S0是S的真子集
–Z：终止状态集，Z是S的子集，可为空集
注：1)非确定主要是指后继状态可有多个。
2) DFA是NFA的特例。
两自动机等价：
–任何两个有限自动机M和M’，若它们识别的语言相同(L(M)=L(M’))，则称M和M’等价。
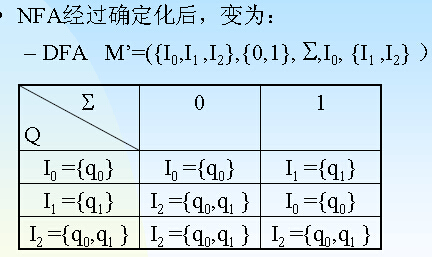
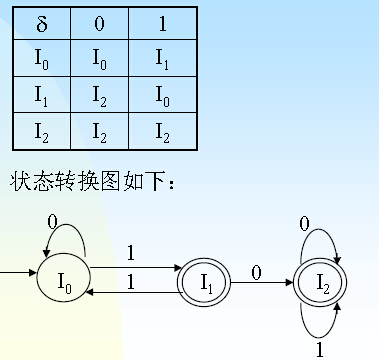
3.2.4NFA确定化
算法
•由NFA M=(S,Σ,f,S0,Z)构造一个等价的DFA M’=(Q, Σ,δ,I0,F）
1.取I0=S0，
2.若状态集Q中有状态Ii={s0,s1,……sj} ,sk∈S , 0 ≤k≤j;而且M机中有f({s0,s1,……sj},a)
= f(s0,a) ∪f(s1,a) ∪……∪f(sj,a)=Υ
={s0,s1,……st} =It，
若It不在Q中，则将It加入Q。
3.重复步骤2，直到Q中无新状态加入为止。
4.取终态F={I | I ∈Q,且I ∩Z <>Φ}
注
1)上述过程可在有限步内完成，因为M机状态的幂集是有限的；
2)上述过程也可用表格法来描述，其中列是字符集Σ中的字符；行是Q中的各状态，开始仅包含I0状态，随着算法的执行，Q的状态逐渐增多直止不再增多为止；表格元素就是δ映射函数。
3)NFA确定化的实质是以原有状态集上的覆盖片(COVER)作为DFA上的一个状态，将原状态间的转换改为覆盖片间的转换，从而将不确定问题确定化。
4)通常，经确定化后，状态数增加，而且可能出现一些等价状态，这时需要化简。
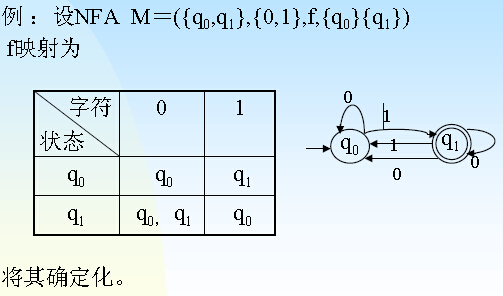
来个例子就很好理解
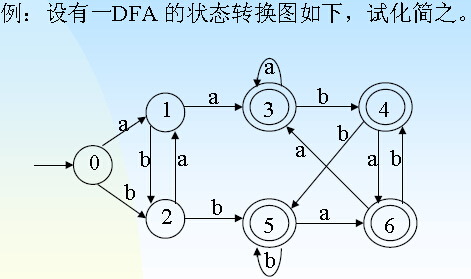
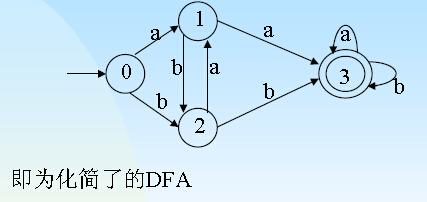
这里写图片描述

3.2.5确定有限自动机的化简（最小化）
(1)化简条件：接受的语言必须相同
(2)化简(最小化)算法基本思想——划分法
–1.将DFA M 中的状态划分为互不相交的子集，每个子集内部的状态都等价；而在不同子集间的状态均不等价。
–2.从每个子集中任选一个状态作为代表，消去其它等价状态。
–3.把那些原来射入其它等价状态的弧改为射入相应的代表状态。
依然来个例子来理解：
这里写图片描述

3.3正规式与有限自动机之间的关系

定理：Σ上的NFA M所能识别的语言L(M)可以用Σ上的正规式来表示。即：对Σ上的NFA M ，可构造一个正规式α，使得L(α)=L(M)
定理：Σ上任何正规式α，存在DFA M使得L(M)=L(α)。即：由正规式α可以构造一个DFA M，使得L(M)＝L(α)
有限自动机M向正规式α的转换
1)把状态转换图的概念拓广，令每条弧上都可以用一个正规式作标记。
2)在M的转换图上加两个结点：x,y。从x用ε弧连接到M的所有初态结点；从M的终态结点用ε弧连接到y。这个新的NFA为M’，且L(M)=L(M’)
3)通过引入的3条有限自动机替换规则逐步消去M’中的所有结点，直到只剩下x和y为止。这样，在x至y的弧线上的标记就是Σ上的正规式，也就是M接受的正规式。
正规式α向确定有限自动机M的转换
1)由正规式α构造一个如下仅有两个结点x,y的状态图。
2)按所引入的3条正规式分裂规则分裂α。
3)重复步骤2直到每个弧上的标记是Σ上的一个字符或ε为止。
4)将所得的NFA M(因为包含ε弧)进行确定化就得到DFA。