树状数组详解

树状数组

树状数组的结构对于初学者而言往往难以理解，我也是最近才认识并了解到这一“默默无闻”的数据结构，C/C++与Java均没有库函数支持，只能手写，但它本身的优势在某些场合却是非常突出的。
假定一个顺序数组A[]，下标为[1]~[N]，按址查询（按下标查询）的时间复杂度为O(1)，而区间求和A[1]+A[2]+...+A[N]的时间复杂度为O(N)。树状数组结构的超强优势在于：使上述两种操作的时间复杂度均为O(lgN)。

数学上的树状数组

现令数组C[]，下标为[1]~[N]：根据顺序数组A[]来构建树状数组C[]。定义如下：
将i用二进制表示，C[i]存储的是从A[i]开始往前数共k个元素的子序和，k指的是二进制i的最低位1的权重。公式为：

算法设计角度

此时，我们需要将下标i转换成二进制来理解，当我们面对二进制下标时，便可以直观地看到每个下标i的k值。
C[1]=C[0001], k=1
C[2]=C[0010], k=10
C[3]=C[0011], k=1
C[4]=C[0100], k=100
C[5]=C[0101], k=1
···
此时我们就可以给出树状数组的另一种描述：C[i]即C[****1....]，'*'表示任意位二进制数1或0，而'.'则表示任意位二进制0。以C[24]即C[11000]为例，我们就可以写出这样的子序和，k为8(1000)，共8项：
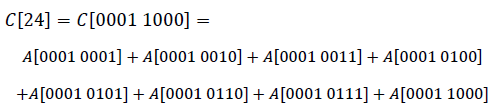它的规律便是一个有公共前缀的Σ求和：

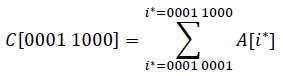
公共前缀为0001，后面均为逐项求和位0001~1000，即从第1项开始累加到第k项。

C[24]的图解

上图中的每个彩色方块，都代表了C[]数组中的一个元素，它们或短或长，长度就是求和项的项数（k值）；灰色方块则代表A[]数组的24个元素。形状其实像二叉树结构，这就是树状数组名称的含义。
注：i为奇数时，必有C[i] = A[i]。

这就是树状数组结构的计算原理，它的关键之处在于：如何求得一个二进制数的最低位1？ 这就要用到lowbit函数。

lowbit函数

求得最低位1其实很简单，因为在计算机中的数据都是以二进制补码形式表示的，对于二进制数i的最低位1，将i和负i进行按位与(&)计算即可，这就是lowbit函数：

int lowbit(int i) {
    // i = 00011000
    // -i = 11101000
    // i&(-i) = 00001000(按位与，即可得到K值，即最低位1的权重)
    return i&(-i);
}

数据结构：动态树状数组（C/C++）

对于树状数组，有两种存储模式：

1. 按地址存储的树状数组（常规的存储思维）；
2. 按内容存储的树状数组。

按地址存储时，是我们正常的存储习惯，比如以上所介绍C[24]的思路，C[24]存放的是A[17]~A[24]的内容的和。这种方式可以很容易根据顺序数组A[]来构建树状数组C[]。
按内容存储时，就比较有趣，这时我们将用地址（即下标）来表示内容。比如顺序数组A[]中存放了若干个数，我们不按正常的下标顺序依次取数，而是构建一个逆映射数组Ar[]，然后将数组A[]所存储的数据视为一个无序集合，并将集合中的每一个元素elem作为Ar[]的下标，即Ar[elem]。并将Ar[elem]置为1，意为elem元素是存在并被存储了的。最后，再根据Ar[]来构建C[]。 Ar[elem]置为n当且仅当A[]数组中有n个elem。

这有点类似于哈希映射key-value结构，此时key指的是数据，value是数据出现的次数的存储（如果你更习惯STL中的unordered_map，那就是first-second结构），但是公共前缀子区间和的特性也是要保留的，这是树状数组特性的根本。
举例说明如下：

// C伪代码
// 示例数组，A[0]没有意义:
#define flase 0
int A[8] = {false, 3, 2, 3, 5, 8, 14, 10};

// 按地址存储的C[]数组:
C[1] = A[1] = 3;
C[2] = A[1] + A[2] = 5;
C[3] = A[3] = 3;
C[4] = A[1] + A[2] + A[3] + A[4] = 13;
C[5] = A[5] = 8;
C[6] = A[5] + A[6] = 22;
C[7] = A[7] = 10;

// 按内容存储的C[]数组:
Ar[0] = false;        
Ar[1] = false;    C[1] = Ar[1] = false;
Ar[2] = 1;        C[2] = Ar[1] + Ar[2] = 1;
Ar[3] = 2;        C[3] = Ar[3] = 2;
Ar[4] = false;    C[4] = Ar[1] + Ar[2] + Ar[3] + Ar[4] = 3;
Ar[5] = 1;        C[5] = Ar[5] = 1;
Ar[6] = false;    C[6] = Ar[5] + Ar[6] = 1;
Ar[7] = false;    C[7] = Ar[7] = false;
Ar[8] = 1;        C[8] = Ar[1] + Ar[2] + Ar[3] +...+ Ar[8] = 5;
Ar[9] = false;    C[9] = false;
Ar[10] = 1;       C[10] = Ar[9] + Ar[10] = 1;
···               ···
Ar[14] = 1;       C[14] = Ar[13] + Ar[14] = 1;

1. 增添/删除元素，并更新数组

现根据A[i]来更新C[i]，因为存储的是若干子序和，所以需要向后更新，以加入并存储A[6]为例：
C[6] = C[0110] = A[0101] + A[0110] = A[5] + A[6]
这里A[6]不仅出现在C[6]的合式里，还会出现在C[8]、C[16]、C[32]、C[64]…等等合式里：
C[8] = A[1] + A[2] + ... + A[8]
C[16] = A[1] + A[2] + ... + A[16]
···
所以要从6开始（包含6），对每一个进位进行更新，这个过程如果不设置数组容量上限的话，将会是无穷无尽的。设置上限为：
#define MAX_INF 0x3f3f3f3f
随后可通过每次自增lowbit(i)，以达到循环设置，下面是更新函数的代码块：

#define MAX_INF ((int)0x3f3f3f3f)
#define TRUE 1
int C[MAX_INF];
void update(int i, int value) {
    // 根据A[i]更新树状数组C。主函数中运行：
    // update(i, A[i]);（按地址存储）
    // update(A[i], TRUE);（按内容存储）
    for (int j = i; j < MAX_INF; j += lowbit(j))
        C[j] += value;
}

删除算法也类似，将update函数的第二个参数传递为相应的负值即可。一次更新，平均时间复杂度为O(lgN)。实际应用时应根据数据规模合理设置上限MAX_INF。

2. 单点查询与单点修改

查询是按地址查询，对于顺序数组来说，这是O(1)的事情。但若没有维护A[]，而只有C[]，则查询的方法如下：

int C[MAX_INF];
int ask(int i) {
    // 从子序和C[i]中剥离出A[i]
    int ret = C[i];
    int k = lowbit(i);
    for (int j = 1; j < k; j = j << 1)
        ret -= C[i-j];
    return ret;
}

以上算法时间复杂度O(lgN)。算法基于剥离公式，感兴趣的童鞋可以用数学方法，或者举例以验证其准确性，即：

1. 当k为1，即i为奇数时，有：A[i] = C[i]
2. 当k大于1，即i为偶数时，有：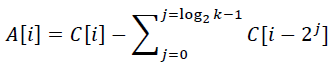

注：按内容存储的树状数组，由于地址（下标）被用来存储内容，每一项内容对应的原数组的地址（下标）在没有维护A数组的情况下，是无法恢复和求得的，故无法按地址访问，只可按内容查询。

若按内容进行查找，可使用按内容存储的树状数组，但是当C[elem]不为0时，elem未必就会存在。比如只有一个元素的集合{1}，其树状数组结构里的C[1], C[2], C[4], C[8]...等的值均为1。此时依旧调用ask函数，但传递的参数应为要查询的内容elem，函数将返回elem的个数。

【注】
按地址存储的树状数组C，不支持按内容查找（效率低）
按内容存储的树状数组C，不可能按地址查找（办不到）

修改的方法是调用update函数：

// 修改：A[i]的值由 old_elem 替换为 new_elem后，对C[]进行修改:
//按地址存储：
update(i, new_elem - old_elem);
//按内容存储：
update(old_elem, -1);
update(new_elem, 1);

3. 区间查询

这是树状数组应用的核心方法。它可以在O(lgN)的时间里，给出任意连续子区间的和，下面列出getsum函数，函数接受一个形参i，返回顺序数组A[1]~A[i]的和，即前i项和：

int getsum(int i) {
    // 按地址存储，则返回顺序数组A的前 i项和。
    // 按内容存储，则返回 i在数组 A中的排序位次，即:
    // 数组 A中小于等于 i的数的个数。
    int ret = 0;
    for (int j = i; j >= 1; j -= lowbit(j))
        ret += C[j];
    return ret;
}

**它的时间复杂度为O(lgN)，这是树状数组最迷人的地方。若要求A[i]~A[i+n-1]的n项和，调用getsum(i+n-1) - getsum(i-1)**即可！