树状数组 求区间最值、求区间和 详解

从代码开始

以下就是树状数组的核心代码。

int lowbit(int x)
{
	return x&-x;
}
void add(int i,int x)
{
	while(i<=n)
	{
		c[i]+=x;
		i+=lowbit(i);
	}
}
int get(int i)
{
	int ans=0;
	while(i)
	{
		ans+=c[i];
		i-=lowbit(i);
	}
	return ans;
}

简介

树状数组能维护区间最值、区间和，查询、增加都是$O(\log n)$，十分常用。
基本思想：树状的分块前缀和（不是

分析代码

add部分（改变某数的值）

$add$ 函数大概表示这样一个功能：
首先将一个数的最后一位 $1$ 进一位（即 $i+=lowbit(i)$部分，其中 $lowbit(i)$ 详见这里）
然后将 $c[i]$ 加上要加的值（可参见下面的图，表示了每个$i+=lowbit(i)$后会到哪里）

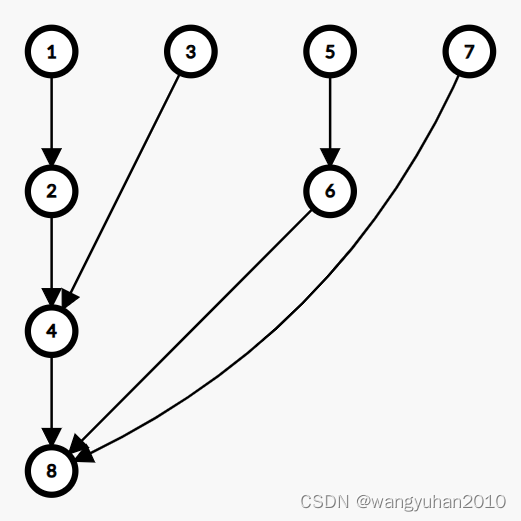
比如，将$5$加上$1$就要将$6$和$8$都加上1

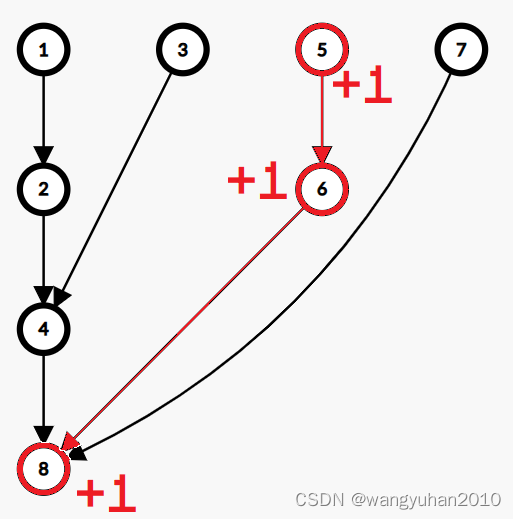
所以，有什么用呢？

get部分(求$1-i$所有数的和)

同理，$get$ 函数表示这样一个功能：
首先将一个数的最后一位 $1$ 变为$0$ 。
然后收集 $c[i]$ 的值（可参见下面的图，绿线表示了每个$i-=lowbit(i)$后会回到哪里）

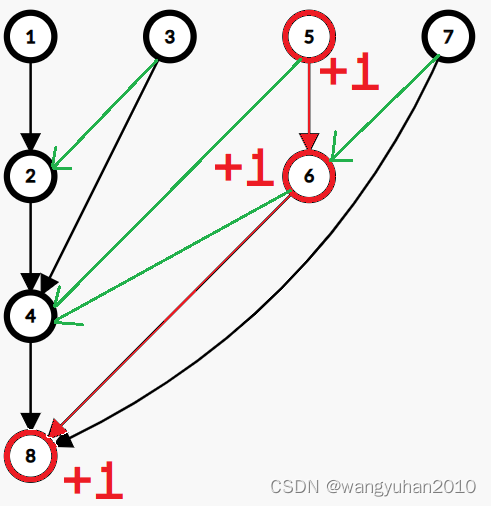
可以发现，如果求$n$,就永远不会沿绿线到$>n$的数，也不会回到$n$的儿子（$n$的儿子的值已经加到$n$中），所以，即可沿路求得$1-n$所有数的和

如果换一种方式，可能会清晰一点。

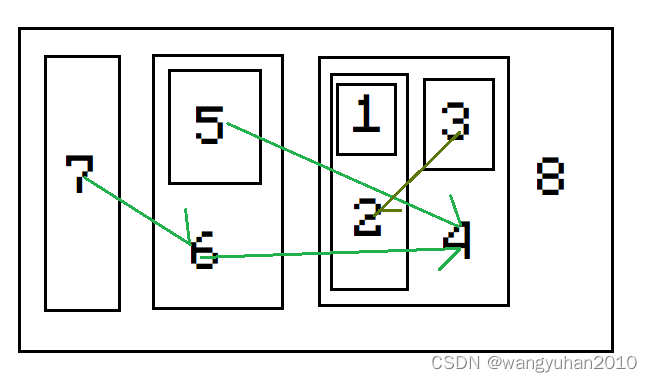
其中，在外面的表示它已经加上了（包括了）里面的值。
例如：求$1-7$的和$=7+(1-6的和)=7+6[包括5]+(1-4的和)=7+6[包括5]+4[包括1-3]$

那么，代码如何实现？

再放一遍代码:

int lowbit(int x){return x&-x;}
void add(int i,int x)
{
	while(i<=n){c[i]+=x;i+=lowbit(i);}
}
int get(int i)
{
	int ans=0;
	while(i){ans+=c[i];i-=lowbit(i);}
	return ans;
}

**

初始数组:相当于$0$加上初始值，只要用$add$函数即可
将某个数增加几:用$add$函数即可
返回一段和 :$get$函数可以求$1-n$的和，因此只要$get(r)-get(l-1)=SUM(1,r)-SUM(1,l-1)=SUM(l,r)$
返回一个数 :只要$get(x)-get(x-1)=a[x]$
将一段增加几:类似差分，增加一段后还要减回来。$add(r,x);add(l,-x)$

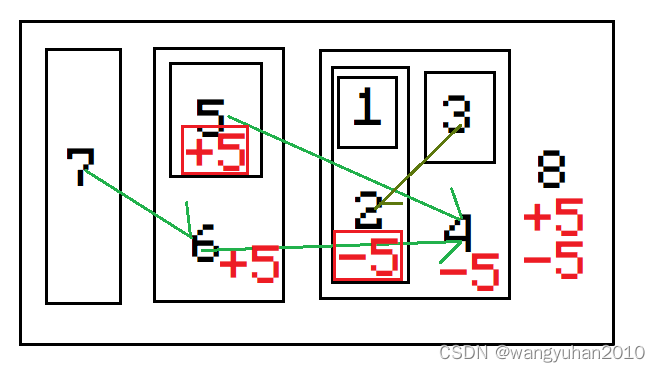
比如,将$[2,5]$增加$5$,结果如上图，其中未被框起来的±$5$是因为包括了要处理的数而被动加减。

如何维护区间最值？

思路:因为是大区间获取最值时会与小区间取$max$，所以可以每次更新时只取儿子的$max$，而不用照顾到父亲的值（与求和不同）

更改add函数 （但是叫updata更合适）

要与儿子们取max进行更新，但不能取全部的儿子，比如更新8时要更新7个，会达到$O(n)$。

比如对于更新$4$，$2\&3$是真儿子，而$1$已经被$2$更新过，不用再更新（因为1一定$<=2$ ）。
经过观察(别问我是怎么观察的)，可得$n$的真儿子为$n-2^x[x<=\log lowbit(n)]$，说人话，就是

  for(int t=1;t<lowbit(i);t<<=1)

所以就简单了。

void add(int i,int x)
{
    c[i]=x;
    for(int t=1;t<lowbit(i);t<<=1)c[i]=max(c[i],c[i-t]);
}

更改get函数

只要找$[l,r]$中真儿子更新即可。

int get(int l,int r)
{
    int ans=a[r];
    while(l<=r)
    {
        ret=max(ret,a[r]);
        for(--r;r-l>=lowbit(r);r-=lowbit(r))ans=max(ans,c[r]);
    }
    return ret;
}