Admission to Exam

Admission to Exam

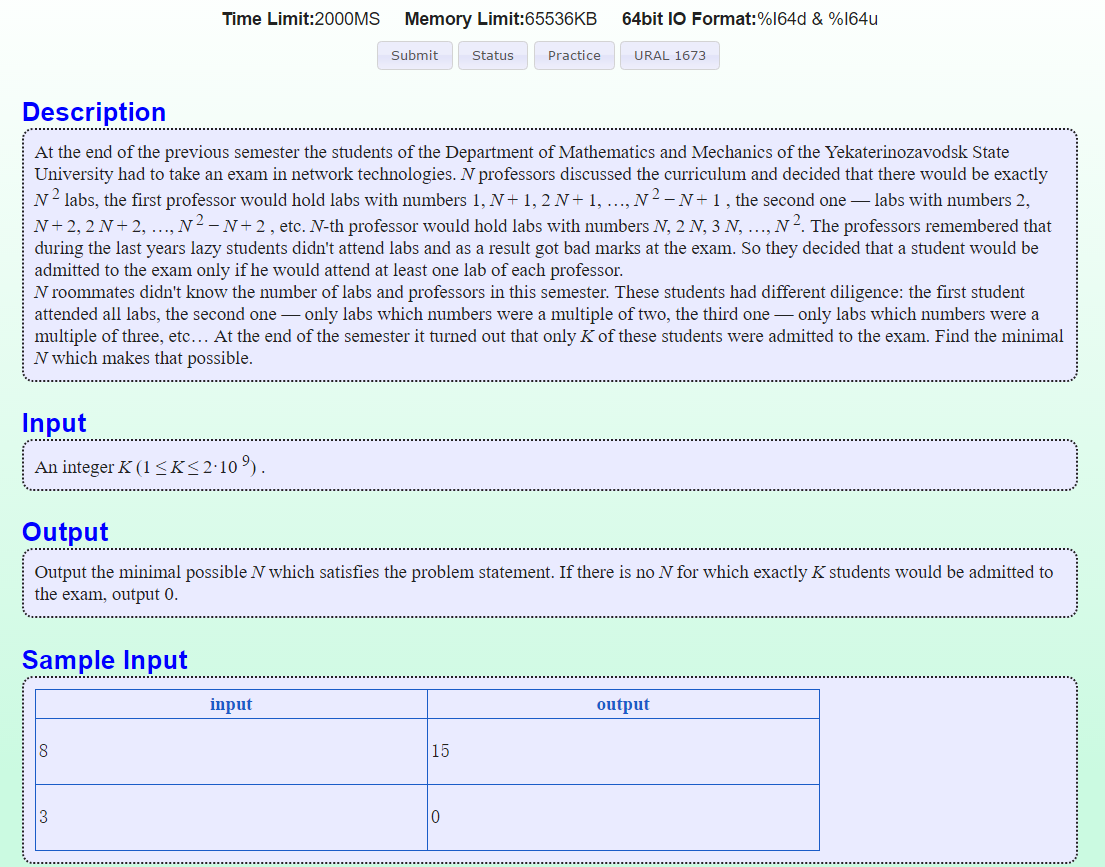
题意：即求一个最小的n，满足n的欧拉函数为k
解法：由于k比较大，可以预处理sqrt（k）中的所有素数，由公式得欧拉函数值=π(pi-1)pi^(m-1），其中pi为约数，可以预处理sqrt（k）中的所有素数，然后再进行划分
.
.
一下为队友代码

#include <cstdio>
#include <map>
using namespace std;

map<long long,long long> a;
long long prime[100010], cnt_prime;
bool b[100010];
long long max(long long a, long long b)
{
    if (a < b) return b;
    return a;
}

long long min(long long a, long long b)
{
    if (a < b) return a;
    return b;
}

void getprime()
{
    for (long long i = 2; i <= 100000; i++)
    {
        if (!b[i]) prime[++cnt_prime] = i;
        for (long long j = 1; j <= cnt_prime && i * prime[j] <= 100000; j++)
        {
            b[i * prime[j]] = true;
            if (i % prime[j] == 0) break;
        }
    }
}

long long count(long long p, long long pos)
{
    if (a[p]) return a[p];
    long long res = 1e18;
    bool ok = false;
    if (pos == 1 && p % 2 == 0)
    {
        long long r = 2, q = p;
        while (q % 2 == 0)
        {
            r = r * 2; q = q / 2;
            long long z = count(q, 2);
            if (z < 1e18) res = min(res, r * z);
        }
    }
    for (long long i = 1; prime[i] * prime[i] <= p + 1; i++)
    {
        if ((p + 1) % prime[i] == 0)
        {
            ok = true; break;
        }
    }
    if (ok)
    for (long long i = max(pos,2); (prime[i] - 1) * (prime[i] - 1) < p; i++)
    {
        if ((prime[i] - 1) * (prime[i] - 1) < p && p % (prime[i] - 1) == 0)
        {
            long long r = prime[i], q = p / (prime[i] - 1); 
            long long z = count(q, i + 1);
            if (z < 1e18)
            res = min(res, r * z);
            while (q % prime[i] == 0)
            {
                r = r * prime[i]; q = q / prime[i];
                z = count(q, i + 1);
                if (z < 1e18)
                res = min(res, r * z);
            }

        }
    }
    else res = p + 1;
    a[p] = res; return res;
}

int main()
{
    long long n;
    scanf("%I64d", &n);
    getprime();
    a[1] = 1; a[2] = 3;
    long long ans = count(n, 1);
    if (ans < 1e18) printf("%I64d\n", ans);
    else printf("0\n");
}