最小生成树_给定一棵树,每次加边,求最小生成树-CSDN博客

参考：勿在浮沙筑高台：http://blog.csdn.net/luoshixian099/article/details/51908175

qwurey：http://blog.csdn.net/yeruby/article/details/38615045

关于图的几个概念定义：

连通图：在无向图中，若任意两个顶点 vi 与 vj 都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点 vi 与 vj 都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
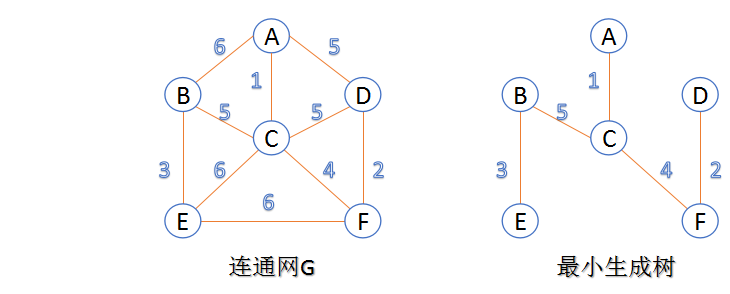
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

下面介绍两种求最小生成树算法

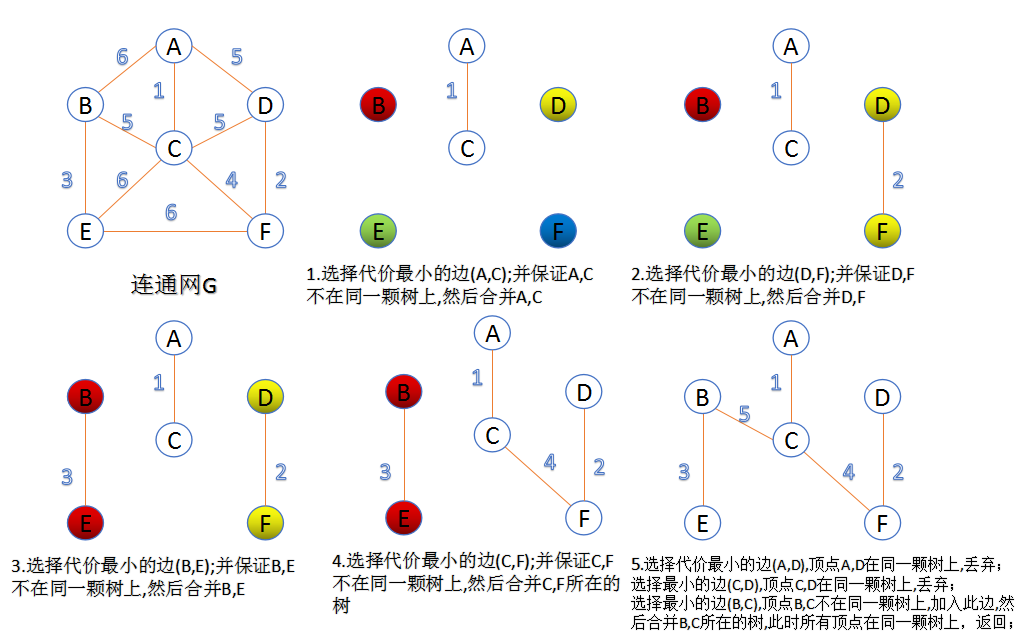
1.Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。
1. 把图中的所有边按代价从小到大排序；
2. 把图中的n个顶点看成独立的n棵树组成的森林；
3. 按权值从小到大选择边，所选的边连接的两个顶点 ui,vi ,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

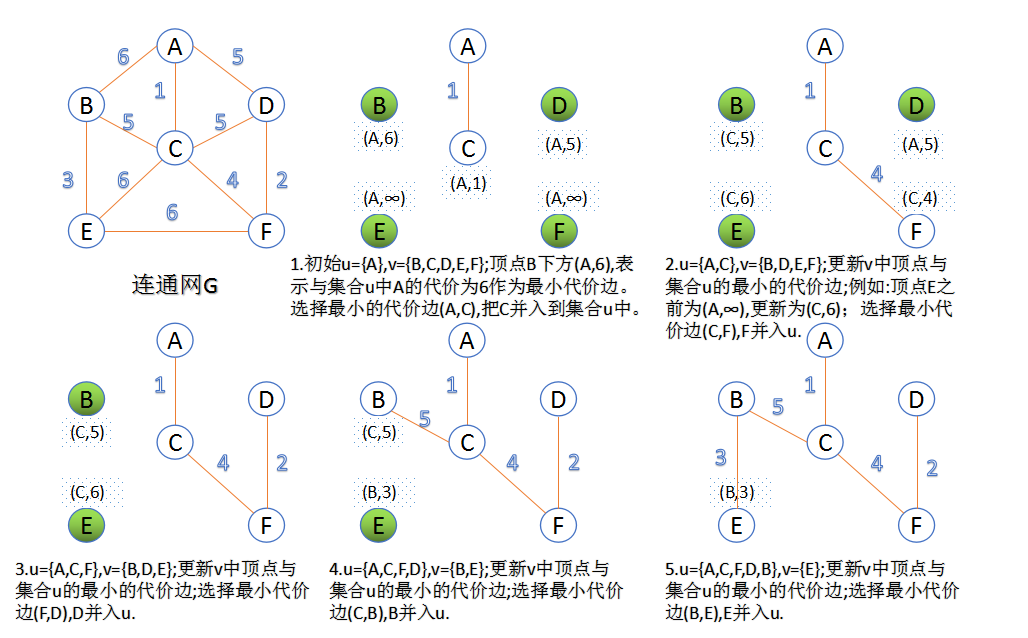
这里写图片描述

2.Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为 V ；初始令集合 u={s},v=V−u ;
在两个集合 u,v 能够组成的边中，选择一条代价最小的边 (u0,v0) ，加入到最小生成树中，并把 v0 并入到集合u中。
重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]
 
 1
2
3
4
5

这里写图片描述

还是prime：

MST（Minimum Spanning Tree，最小生成树）问题有两种通用的解法，Prim算法就是其中之一，它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

用图示和代码说明：

初始状态：

设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST

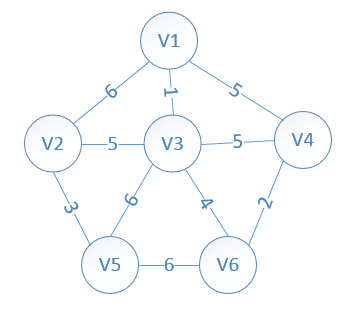
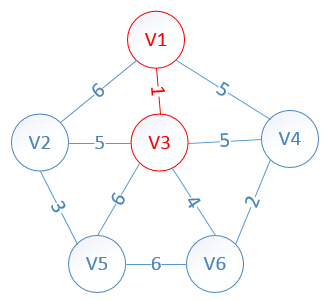
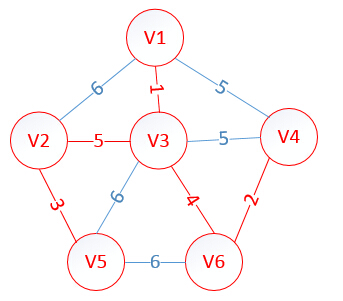
我们假设V1是起始点，进行初始化（*代表无限大，即无通路）：

lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=*，lowcost[6]=*

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

明显看出，以V3为终点的边的权值最小=1，所以边<mst[3],3>=1加入MST

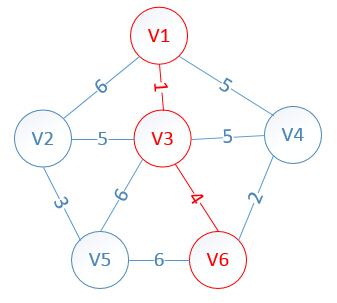
此时，因为点V3的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST

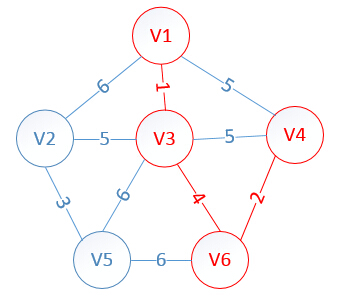
此时，因为点V6的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST

此时，因为点V4的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

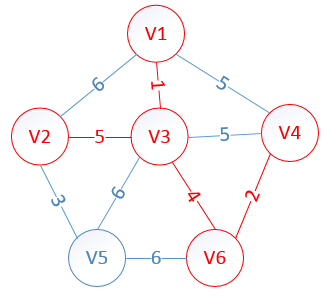
明显看出，以V2为终点的边的权值最小=5，所以边<mst[2],2>=5加入MST

此时，因为点V2的加入，需要更新lowcost数组和mst数组：

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

很明显，以V5为终点的边的权值最小=3，所以边<mst[5],5>=3加入MST

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

至此，MST构建成功，如图所示：

例题：hdu1233 还是畅通工程

prime ac代码：

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<math.h>
#include<string.h>
using namespace std;
#define INF 0x3f3f3f3f

int cost[1005][1005];//cost表示边e=（u，v）的权值
int mincost[1005];//最小权值
bool used[1005];//顶点i是否包含在集合x中
int V;//顶点数

int prime(){
    for(int i=0;i<V;i++)
    {
        mincost[i]=INF;
        used[i]=false;
    }
    mincost[0]=0;
    int res=0;
    int v=0;
    while(v!=-1)
    {
        v=-1;
        //从不属于x的顶点中选取从x到其权值最小的顶点
        for(int u=0;u<V;u++)
        {
            if(!used[u]&&(v==-1||mincost[u]<mincost[v]))
                v=u;
        }
        used[v]=true;//把顶点v加进x
        res+=mincost[v];//把边加进结果里
        for(int u=0;u<V;u++){
            mincost[u]=min(mincost[u],cost[v][u]);
        }
    }
    return res;
}
int main()
{
    while(~scanf("%d",&V)&&V!=0)
    {
        for(int i=0;i<V*(V-1)/2;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            cost[a-1][b-1]=c;
            cost[b-1][a-1]=c;
        }
        printf("%d\n",prime());
    }
    return 0;
}

Kruskal ac代码：

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=10005;
struct node { int from,to,len;} edge[maxn];//储存边的数据结构
int n,fa[maxn],m,ans,q;
bool cmp(node a,node b) { return a.len<b.len; }//边按从小到大的顺序排列
int Find(int x)
{
    if(fa[x]==x) return x;
    return fa[x]=Find(fa[x]);
}
void Merge(int x,int y)
{
    x=Find(x),y=Find(y);
    if(x!=y) fa[y]=x;
}
int kruskal()
{
    sort(edge,edge+m,cmp);//边排序
    for(int i=0;i<=n;i++) fa[i]=i;//初始化并查集
    ans=0;
    for(int i=0;i<m;i++)//一条边的两个端点不在同一个集合，则选它，并合并端点
        if(Find(edge[i].from)!=Find(edge[i].to)) Merge(edge[i].from,edge[i].to),ans+=edge[i].len;
    return ans;
}
int main()
{
    while(cin>>n,n)
    {
        m=n*(n-1)/2;
        for(int i=0;i<m;i++) cin>>edge[i].from>>edge[i].to>>edge[i].len;
        cout<<kruskal()<<endl;
    }
    return 0;
}