[线性代数]行列式(mooc秦静老师讲解)

本内容源于秦静老师的《线性代数》mooc，古之有云：学而不思则罔，思而不学则殆。
主要讲解，思、学、罔、殆。
思：“田”

1.行列式概念

行列式概念起源于为了解决线性方程组求解，掌握这个概念，会二阶行列式对角线展开法，三阶行列式也会展开，也算行列式能基本入门了。

这类题目，也属于这种行列式展开的题目。

2.n阶行列式

三阶行列式我们会用对角线展开了，但是到n阶行列式，还能用对角线展开吗？不能，老师就讲到按照行列展开进行计算，也就是代数余子式。余子式与代数余子式的区别。
代数余子式就是在余子式的基础上有那个(-1)^(i+j)次。下面按照行列式行列展开就可以得出n阶行列式的定义

然后秦静老师的课后作业也非常应景，

也就是把我上面哪个D背出就行啦。

3.特殊行列式的计算

3.1对角行列式

行列式的值a11a22…ann

3.2上(下)三角行列式

下三角可以按照行列式第一行展开，上三角可以按照行列式最后一行展开。答案都是：

a11a22....ann

3.3 斜三角行列式

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200403121659525.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6L
秦静老师说过一句，先给题目相相面，结果发现，第一行有一个，第二行有两个，…第n行有n个，因此我按照第一行进行展开，注意代数余子式,得出答案。

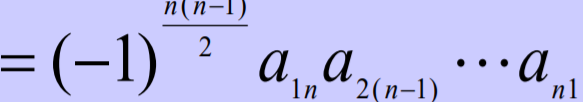
3.4 行列式练习

按照行列式进行展开，这个行列式按照第一列进行展开，然后运用三角行列式，得出最后答案


看见这个，也只需要，按照定义进行展开，就可以了。这个答案最好记忆一下。


这类小题，直接可以变相利用上课讲的内容运算求解

第一题：a1a2...an
第二题：(a2a3-b2b3)^2

4.行列式的性质

• (性质1)行列式转置的值等于行列式的值
• (性质2)互换两行，行列式变号
• (推论)行列式中有两行元素完全相同，则行列式为0
• (性质3)用数k乘行列式某一行中所有元素，等于用k乘行列式
• (推论)某一行的所有元素的公因子可以提到行列式符号的外面。
• (性质4)行列式某一行元素加上另一行对应元素的k倍，行列式的值不变。
• (性质5)若行列式某一行的元素是两数之和，则行列式可拆成两个行列式的和。
• (推论)若行列式某一行的元素都是m个元素的和，则行列式可以写成m个行列式的和。

到后面我们做初等行变换会用到粗体的三个。

按照行列式的定义可以脱口而出i=j等于D，i≠j等于0。2和3本质相同都是i≠j。

5.行列式的计算

我们学会用基本的技巧就是可以为了更好的展开

6.克莱姆法则

克莱姆法则有三个结论，分别是当D≠0时，方程组有解，有唯一解，解是D1/D,D2/D…以此类推。讲到齐次线性方程组时，就是搞明白零解与非零解。D≠0，方程组有唯一0解。D=0，方程有非零解。为什么分零解和非零解，因为非零解换句话就是无穷解！

7.范德蒙行列式

探到范德蒙行列式，了解它长什么样子。

这是解的形式，

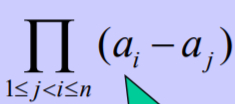
练习1

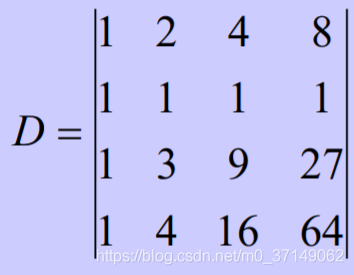
把它转置一下，然后按着第二行开始进行做运算
(1-2)(3-2)(4-2)(3-1)(4-1)(4-3)=-12

练习2

(b-a)(c-a)(c-b)

8.逆序数与行列式

从逆序数来重新认识行列式，这是很旧的书才会讲的，如果要了解逆序数，那就必须先要了解逆序。逆序就是在一个标准顺序情况下，两个元素顺序如果不同，那么这两个元素就构成了逆序。而逆序数就是去求解所有元素逆序相加和。然后就倒出逆序数了。
要重新理解行列式，那就肯定涉及这个：

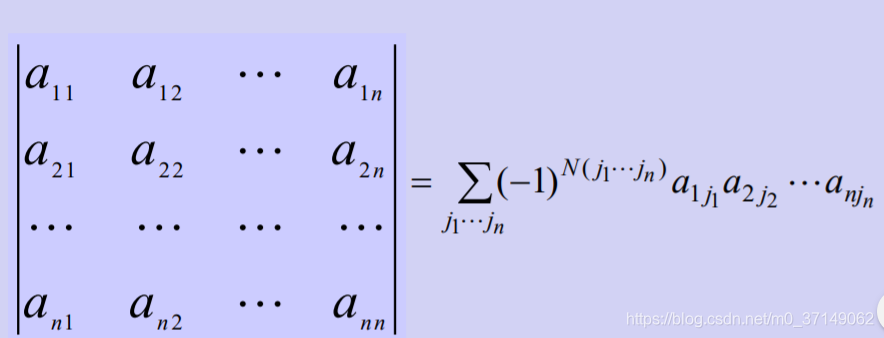
这就是逆序数对行列式的重新构造。