2.尾部的零

题目：设计一个算法，计算出n阶乘中尾部零的个数

样例： 11! = 39916800 ，因此应该返回 2

挑战：O(logN)的时间复杂度

    首先，我用了最笨的方法，源码如下：

class Solution {
public:
    /*
     * @param n: A long integer
     * @return: An integer, denote the number of trailing zeros in n!
     */
    long long trailingZeros(long long n) {
        long long sum=1;
        int result=0;
        while(n){
            sum=sum*n;
            n=n-1;
        }
        while(1){
            if(sum%10==0)
            {
                result=result+1;
                sum=sum/10;
            }else{
                break;
            }
        }
        return result;
    }
};

    先把和sum算出来,然后在每次除以10，如果余数为0则说明尾部有一个0，最后通过result累加得到最终值。可是结果显示

Time Limit Exceeded，并提示：你的代码运行时间超过了限制，检查你的时间复杂度。TLE通常是由死循环造成的，思考一下你的时间复杂度是否是最优的。不对不对不对，事情没有那么简单。。。

    参考网上其他大神的思想如下：

算法3：科学思想

反思&对比

这个算法真的是感触很深，对平时很多习以为常的公式、道理有了非常直观的认识，因此对自己的冲击很大，也促进了思考的进步。

提交算法2的代码，发现前面的简单测试都能通过，但是数值5555550000000测试失败。特别是实现了时间复杂度O(logN)的算法3之后，才发现两者时间开销差别真的是很大。

重新分析

1、2、3、4、5、6、7、8、9、10、11、...

• 1

1、分析上面的数列可知，每5个数中会出现一个可以产生结果中0的数字。把这些数字抽取出来是：

...、5、...、10、...、15、...、20、...、25、...

• 1

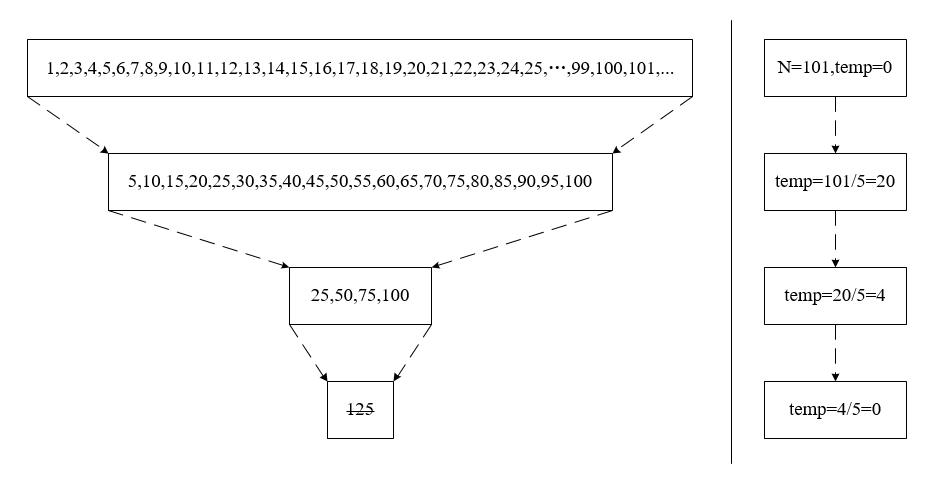
这些数字其实是都能满足5*k的数字，是5的倍数。统计一下他们的数量：n1=N/5。比如如果是101，则101之前应该是5,10,15,20,...,95,100共101/5=20个数字满足要求。

整除操作满足上面的数量统计要求。

2、将1中的这些数字化成5*(1、2、3、4、5、...)的形式，内部的1、2、3、4、5、...又满足上面的分析：每5个数字有一个是5的倍数。抽取为：

...、25、...、50、...、75、...、100、...、125、...

• 1

而这些数字都是25的倍数（5的2次幂的倍数），自然也都满足5*k的要求。
这些数字是25、50、75、100、125、...=5*(5、10、15、20、25、...)=5*5*(1、2、3、4、5、...)，内部的1、2、3、4、5、...又满足上面的分析，因此后续的操作重复上述步骤即可。
统计一下第二次中满足条件的数字数量：n2=N/5/5，101/25=(101/5)/5=4。
因为25、50、75、100、125、...它们都满足相乘后产生至少两个0，在第一次5*k分析中已经统计过一次。对于N=101，是20。因此此处的5*5*k只要统计一次4即可，不需要根据25是5的二次幂统计两次。
后面的125,250,...等乘积为1000的可以为结果贡献3个0的数字，只要在5*5*k的基础上再统计一次n3=((N/5)/5)/5即可。

3、第三次
其实到这里已经不用再写，规律已经很清楚了。对于例子N=101，只要根据规律进行101/125=((101/5)/5)/5=4/5=0，退出统计。因此最终结果是20+4=24。计算结束。

算法3代码

下面编写打码实现上面的思想。

public class Solution {

    /*
     * param n: As desciption return: An integer, denote the number of trailing
     * zeros in n!
     */
    public long trailingZeros(long n) {
        // write your code here
        long count = 0;
        long temp=n/5;
        while (temp!=0) {
            count+=temp;
            temp/=5;
        }
        return count;
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17

代码分析：
算法中每次循环均有除以5的操作，也就是每次都会将所要处理的数据量缩小至上一次的1/5，容易推知时间复杂度为O(logN)。

至此，问题解决。

tips

关于测试代码，按照上一篇文章的介绍，如果使用Main函数调用Solution:trailingZeros()函数，在传入参数较小的时候，不会有什么问题，如下：

public class Test{
    public static void main(String args[]){
        Solution s=new Solution();
        long result=s.trailingZeros(11);
        System.out.println(result);
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7

因为11不超过int类型的最大长度，所以并不会报错。但是如果是5555550000000，则会报错:

The literal 5555550000000 of type int is out of range 

• 1

将数值进行强制类型转换也不行：long inNum=(long)5555550000000;。
一种解决方法是使用Scanner直接读取数值。
改进后的代码如下：

public class Test{
    public static void main(String args[]){
        Solution s=new Solution();
        Scanner scanner=new Scanner(System.in);
        long result=s.trailingZeros(scanner.nextLong());
        System.out.println(result);
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

这时输入5555550000000则不会报错。
另外，如果需要的话，可使用System.currentTimeMillis();观察代码执行时间。

    最终代码：

  

 class Solution {
public:
    /*
     * @param n: A long integer
     * @return: An integer, denote the number of trailing zeros in n!
     */
    long long trailingZeros(long long n) {
        long long numFactor5 = 0;
        
        while (n >= 5)
        {
            n = n / 5;
            numFactor5 += n;
        }

        return numFactor5;
    }
};

很强！分析问题，找规律