模拟退火算法

模拟退火算法原理

爬山法是一种贪婪的方法，对于一个优化问题，其大致图像(图像地址)如下图所示： 
 
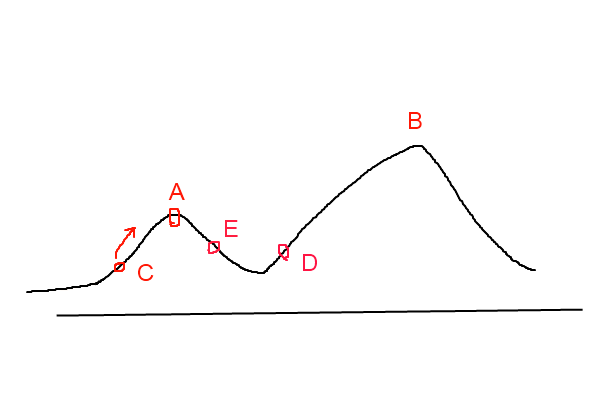
其目标是要找到函数的最大值，若初始化时，初始点的位置在 C 处，则会寻找到附近的局部最大值 A 点处，由于 A 点出是一个局部最大值点，故对于爬山法来讲，该算法无法跳出局部最大值点。若初始点选择在 D 处，根据爬山法，则会找到全部最大值点 B 。这一点也说明了这样基于贪婪的爬山法是否能够取得全局最优解与初始值的选取由很大的关系。

模拟退火算法(Simulated Annealing, SA)的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减小，粒子的慢慢趋于有序，最终，当固体处于常温时，内能达到最小，此时，粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。

模拟退火算法从某一较高的温度出发，这个温度称为初始温度，伴随着温度参数的不断下降，算法中的解趋于稳定，但是，可能这样的稳定解是一个局部最优解，此时，模拟退火算法中会以一定的概率跳出这样的局部最优解，以寻找目标函数的全局最优解。如上图中所示，若此时寻找到了 A 点处的解，模拟退火算法会以一定的概率跳出这个解，如跳到了 D 点重新寻找，这样在一定程度上增加了寻找到全局最优解的可能性。

模拟退火算法

模拟退火算法过程

(1)随机挑选一个单元 k ，并给它一个随机的位移，求出系统因此而产生的能量变化 ΔEk 。 
(2)若 ΔEk⩽0 ，该位移可采纳，而变化后的系统状态可作为下次变化的起点； 
若 ΔEk>0 ，位移后的状态可采纳的概率为 

Pk=11+e−ΔEk/T

式中 T 为温度，然后从 (0,1) 区间均匀分布的随机数中挑选一个数 R ，若 R<Pk ，则将变化后的状态作为下次的起点；否则，将变化前的状态作为下次的起点。 
(3)转第(1)步继续执行，知道达到平衡状态为止。

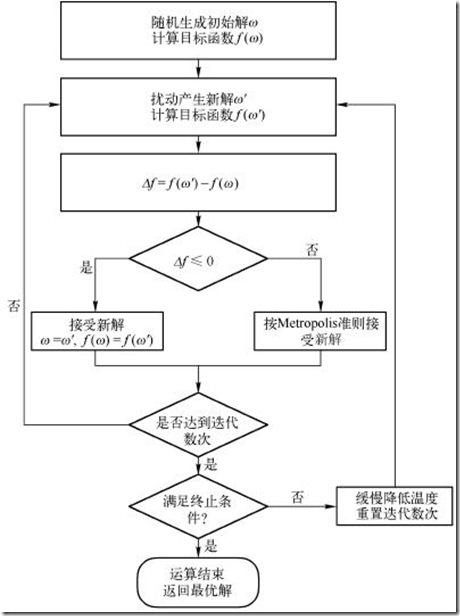
模拟退火算法流程

1.旅行商问题

根据概率产生新解主要包含两个途径：二交换和三交换 
二交换是在TSP回路中选择两个城市直接交换 
三交换是在TSP回路中选择三个点，p1,p2,p3，然后将p1,p2之间的城市直接与p3之前对应长度的城市交换 
这里产生新解的方法不唯一，只要能够保证产生的新解可以包含最优解所在的解空间即可 
是否接受新解主要包含两种情况： 
新解比历史最优解好，则百分百接受新解 
新解比当前解好，没历史最优解好，则以一定概率接受新解，并且随着温度的降低。接受的概率也会降低。 

如下是TSP代码。

swap.m
function [ newpath , position ] = swap( oldpath , number )
% 对 oldpath 进 行 互 换 操 作
% number 为 产 生 的 新 路 径 的 个 数
% position 为 对 应 newpath 互 换 的 位 置
m = length( oldpath ) ; % 城 市 的 个 数
newpath = zeros( number , m ) ;
position = sort( randi( m , number , 2 ) , 2 ); % 随 机 产 生 交 换 的 位 置
for i = 1 : number
newpath( i , : ) = oldpath ;
% 交 换 路 径 中 选 中 的 城 市
newpath( i , position( i , 1 ) ) = oldpath( position( i , 2 ) ) ;
newpath( i , position( i , 2 ) ) = oldpath( position( i , 1 ) ) ;
end


pathfare.m
function [ objval ] = pathfare( fare , path )
% 计 算 路 径 path 的 代 价 objval
% path 为 1 到 n 的 排 列 ，代 表 城 市 的 访 问 顺 序 ；
% fare 为 代 价 矩 阵 ， 且 为 方 阵 。
[ m , n ] = size( path ) ;
objval = zeros( 1 , m ) ;
for i = 1 : m
for j = 2 : n
objval( i ) = objval( i ) + fare( path( i , j - 1 ) , path( i , j ) ) ;
end
objval( i ) = objval( i ) + fare( path( i , n ) , path( i , 1 ) ) ;
end


distance.m
function [ fare ] = distance( coord )
% 根 据 各 城 市 的 距 离 坐 标 求 相 互 之 间 的 距 离
% fare 为 各 城 市 的 距 离 ， coord 为 各 城 市 的 坐 标
[ v , m ] = size( coord ) ; % m 为 城 市 的 个 数
fare = zeros( m ) ;
for i = 1 : m % 外 层 为 行
for j = i : m % 内 层 为 列
fare( i , j ) = ( sum( ( coord( : , i ) - coord( : , j ) ) .^ 2 ) ) ^ 0.5 ;
fare( j , i ) = fare( i , j ) ; % 距 离 矩 阵 对 称
end
end


myplot.m
function [ ] = myplot( path , coord , pathfar )
% 做 出 路 径 的 图 形
% path 为 要 做 图 的 路 径 ，coord 为 各 个 城 市 的 坐 标
% pathfar 为 路 径 path 对 应 的 费 用
len = length( path ) ;
clf ;
hold on ;
title( [ '近似最短路径如下，路程为' , num2str( pathfar ) ] ) ;
plot( coord( 1 , : ) , coord( 2 , : ) , 'ok');
pause( 0.4 ) ;
for ii = 2 : len
plot( coord( 1 , path( [ ii - 1 , ii ] ) ) , coord( 2 , path( [ ii - 1 , ii ] ) ) , '-b');
x = sum( coord( 1 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
y = sum( coord( 2 , path( [ ii - 1 , ii ] ) ) ) / 2 ;
text( x , y , [ '(' , num2str( ii - 1 ) , ')' ] ) ;
pause( 0.4 ) ;
end
plot( coord( 1 , path( [ 1 , len ] ) ) , coord( 2 , path( [ 1 , len ] ) ) , '-b' ) ;
x = sum( coord( 1 , path( [ 1 , len ] ) ) ) / 2 ;
y = sum( coord( 2 , path( [ 1 , len ] ) ) ) / 2 ;
text( x , y , [ '(' , num2str( len ) , ')' ] ) ;
pause( 0.4 ) ;
hold off ;


clear;
% 程 序 参 数 设 定
Coord = ... % 城 市 的 坐 标 Coordinates
[ 0.6683 0.6195 0.4    0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ; ...
  0.2536 0.2634 0.4439 0.1463 0.2293 0.761  0.9414 0.6536 0.5219 0.3609 ] ;
t0 = 1 ; % 初 温 t0
iLk = 20 ; % 内 循 环 最 大 迭 代 次 数 iLk
oLk = 50 ; % 外 循 环 最 大 迭 代 次 数 oLk
lam = 0.95 ; % λ lambda
istd = 0.001 ; % 若 内 循 环 函 数 值 方 差 小 于 istd 则 停 止
ostd = 0.001 ; % 若 外 循 环 函 数 值 方 差 小 于 ostd 则 停 止
ilen = 5 ; % 内 循 环 保 存 的 目 标 函 数 值 个 数
olen = 5 ; % 外 循 环 保 存 的 目 标 函 数 值 个 数
% 程 序 主 体
m = length( Coord ) ; % 城 市 的 个 数 m
fare = distance( Coord ) ; % 路 径 费 用 fare
path = 1 : m ; % 初 始 路 径 path
pathfar = pathfare( fare , path ) ; % 路 径 费 用 path fare
ores = zeros( 1 , olen ) ; % 外 循 环 保 存 的 目 标 函 数 值
e0 = pathfar ; % 能 量 初 值 e0
t = t0 ; % 温 度 t
for out = 1 : oLk % 外 循 环 模 拟 退 火 过 程
ires = zeros( 1 , ilen ) ; % 内 循 环 保 存 的 目 标 函 数 值
for in = 1 : iLk % 内 循 环 模 拟 热 平 衡 过 程
[ newpath , v ] = swap( path , 1 ) ; % 产 生 新 状 态
e1 = pathfare( fare , newpath ) ; % 新 状 态 能 量
% Metropolis 抽 样 稳 定 准 则
r = min( 1 , exp( - ( e1 - e0 ) / t ) ) ;
if rand < r
path = newpath ; % 更 新 最 佳 状 态
e0 = e1 ;
end
ires = [ ires( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
% 内 循 环 终 止 准 则 ：连 续 ilen 个 状 态 能 量 波 动 小 于 istd
if std( ires , 1 ) < istd
break ;
end
end
ores = [ ores( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量
% 外 循 环 终 止 准 则 ：连 续 olen 个 状 态 能 量 波 动 小 于 ostd
if std( ores , 1 ) < ostd
break ;
end
t = lam * t ;
end
pathfar = e0 ;
% 输 入 结 果
fprintf( '近似最优路径为：\n ' )
%disp( char( [ path , path(1) ] + 64 ) ) ;
disp(path)
fprintf( '近似最优路径路程\tpathfare=' ) ;
disp( pathfar ) ;
myplot( path , Coord , pathfar ) ;

另外附几题算法题，体会一下模拟退火：

POJ 1379 Run Away

题目：找出一点，距离所有所有点的最短距离最大

#include<iostream>  
#include<cstdio>  
#include<cstring>  
#include<queue>  
#include<cmath>  
#include<string>  
#include<vector>  
#include<algorithm>  
#include<map>  
#include<set>  
#include<ctime>  
#define maxn 200005  
#define eps 1e-8  
#define inf 2000000000  
#define LL long long  
#define zero(a) fabs(a)<eps  
#define MOD 19901014  
#define N 1000005  
#define pi acos(-1.0)  
using namespace std;  
int t,n;  
double X,Y;  
double best[50];  
struct Point{  
    double x,y;  
    bool check(){  
        if(x>-eps&&x<eps+X&&y>-eps&&y<eps+Y)  
            return true;  
        return false;  
    }  
}p[1005],tp[50];  
double dist(Point p1,Point p2){  
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));  
}  
double slove(Point p0){  
    double ans=inf;  
    for(int i=0;i<n;i++)  
        ans=min(ans,dist(p[i],p0));  
    return ans;  
}  
int main(){  
    scanf("%d",&t);  
    srand(time(NULL));  
    while(t--){  
        scanf("%lf%lf%d",&X,&Y,&n);  
        for(int i=0;i<n;i++)  
            scanf("%lf%lf",&p[i].x,&p[i].y);  
        for(int i=0;i<15;i++){  
            tp[i].x=(rand()%1000+1)/1000.0*X;  
            tp[i].y=(rand()%1000+1)/1000.0*Y;  
            best[i]=slove(tp[i]);  
        }  
        double step=max(X,Y)/sqrt(1.0*n);  
        while(step>1e-3){  
            for(int i=0;i<15;i++){  
                Point cur,pre=tp[i];  
                for(int j=0;j<35;j++){  
                    double angle=(rand()%1000+1)/1000.0*2*pi;  
                    cur.x=pre.x+cos(angle)*step;  
                    cur.y=pre.y+sin(angle)*step;  
                    if(!cur.check()) continue;  
                    double tmp=slove(cur);  
                    if(tmp>best[i]){  
                        tp[i]=cur;  
                        best[i]=tmp;  
                    }  
                }  
            }  
            step*=0.85;  
        }  
        int idx=0;  
        double ans=0;  
        for(int i=0;i<15;i++){  
            if(best[i]>ans){  
                ans=best[i];  
                idx=i;  
            }  
        }  
        printf("The safest point is (%.1f, %.1f).\n",tp[idx].x,tp[idx].y);  
    }  
    return 0;  
}  

hdu 5017

链接： 点击打开链接

求一个椭球面上的一个点到原点的最短距离。

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
 
using namespace std;
const double eps = 1e-8;
const double r = 0.99;  //降温速度
const int dx[] = { 0, 0, 1, -1, 1, -1, 1, -1 };
const int dy[] = { 1, -1, 0, 0, -1, 1, 1, -1 };
double a, b, c, d, e, f;
 
double dis(double x, double y, double z) {
    return sqrt(x * x + y * y + z * z);
}
 
//已知x,y,求z
double getz(double x, double y) {
    double A = c, B = e * x + d * y,
        C = a * x * x + b * y * y + f * x * y - 1;
    double delta = B * B - 4 * A * C;
    if (delta < 0) return 1e60;
    double z1 = (-B + sqrt(delta)) / 2 / A,
        z2 = (-B - sqrt(delta)) / 2 / A;
    if (z1 * z1 < z2 * z2) return z1;
    else return z2;
}
 
double solve() {
    //模拟退火
    double step = 1;    //步长
    double x = 0, y = 0, z;
    while (step > eps) {
        z = getz(x, y);
        for (int i = 0; i < 8; i++) {
            double nx = x + dx[i] * step,
                ny = y + dy[i] * step,
                nz = getz(nx, ny);
            if (nz > 1e30) continue;
            if (dis(nx, ny, nz) < dis(x, y, z)) {
                x = nx; y = ny; z = nz;
            }
        }
        step *= r;
    }
    return dis(x, y, z);
}
 
int main() {
    while (scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &e, &f) != EOF) {
        printf("%.8f\n", solve());
    }
    return 0;
}