最小生成树—Prim算法和Kruskal算法 (理解)

 一个带权连通无向图中可能有多棵生成树，所有生成树中具有边上的权值之和最小的树称为图的最小生成树。n个 顶点的连通图的生成树有n个顶点、n-1条边，性质如下：1.不能有回路2.一个图的最小生成树不一定是唯一的，可能有多个。

prim算法——让树慢慢变大 

图G的顶点集合为U，生成树的集合为V。
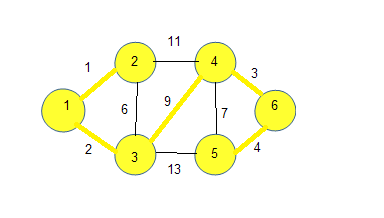
1.在U中选择一个顶点a加入V中。
2.向外（U-V）找到一个点b，使ab之间权值最小，把b也加入V中。
3.再以V中的点向外（U-V）寻找点使这个点与V权值最小并把点加入V中，以此类推，直到所有的顶点加入V中。

算法分析：

1.任意一个顶点开始构造生成树，将此顶点加入生成树中，用一维数组visit来标记哪些顶点已经加入了生成树。
2.用dis数组记录生成树到各个顶点的距离，（注意Dijkstra算法记录的才是源点到各个顶点的距离）初始化dis数组。
3.从dis数组中选出离生成树最近（权值最小）的顶点（j）加入到生成树中【即在数组dis中找最小值】，再以j为中间点，更新生成树到每个非树顶点的距离（即松弛更新的过程），即如果dis[k]>e[j][k]则更新dis[k]=e[j][k]。
4.重复第三步，直到生成树中有n个顶点为止。

代码实现：

#include<iostream>
#include<cstring>
using namespace std;
int n,m,u,v,w;
int e[111][111],dis[111],visit[111];
const int inf=9999999;
//初始化
void init()
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(i==j)
				e[i][j]=0;
			else
				e[i][j]=inf;
		}
	}
}
//prim算法
void prim()
{
	int i,j,k,minn;
	//初始化dis数组，这里是1号点到各个顶点的初始距离，因为当前的生成树中只有1号顶点。
	for(i=1;i<=n;i++)
	{
		dis[i]=e[1][i];
	} 
	memset(visit,0,sizeof(visit));
	//将一号顶点加入生成树
	visit[1]=1;//标记已加入。 
	int count=1,sum=0;//count记录树中的顶点的个数，sum记录路径之和。
	while(count<n)
	{
		minn=inf;
		for(i=1;i<=n;i++)
		{
			if(visit[i]==0&&dis[i]<minn)
			{
				minn=dis[i];
				j=i;
			}
		}
		visit[j]=1;
		count++;
		sum=sum+dis[j];
		//扫描当前顶点j所有的边，再以j为中间点，更新生成树到每个非树顶点的距离
		for(k=1;k<=n;k++)
		{
			if(visit[k]==0&&dis[k]>e[j][k])
				dis[k]=e[j][k];
		} 
	} 
	cout<<sum<<endl;
}
int main()
{
	int i,j,k;	
	cin>>n>>m;
	//初始化 
	init();
	//开始读入边 
	for(i=1;i<=m;i++)
	{
		cin>>u>>v>>w;
		//注意无向图，所以需要将边反向再存储一遍
		e[u][v]=w;
		e[v][u]=w;  
	}
	//prim核心代码
	prim();
	return 0;
}

 kruskal算法 ——把森林合并为树

算法分析：把题目中所给的边按照权值从小到大排序，每次从剩余的边中选取权值较小且边的两个顶点不在同一集合内的边（就是不产生回路的边），加入到生成树中，直到加入了n-1条边。

代码实现：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct edge{
	int u,v,w;
}e[111];
int n,m;
int pre[111];
//初始化
void init()
{
	for(int i=1;i<=n;i++)
	{
		pre[i]=i;
	}
}
//并查集寻找祖先的函数 
int find(int v)
{
	if(pre[v]==v)
		return v;
	else
	{
		pre[v]=find(pre[v]);
		return pre[v];
	}
} 
//并查集的合并
int merge(int u,int v)
{
	int t1=find(u);
	int t2=find(v);
	if(t1!=t2) 
	{
		pre[t2]=t1;
		return 1; 
	}
	return 0;
} 
//对权值进行排序
bool cmp(edge a,edge b)
{
	return a.w<b.w;
} 
int main()
{
	int i;
	cin>>n>>m;
	for(i=1;i<=m;i++)
	{
		cin>>e[i].u>>e[i].v>>e[i].w;
	}
	sort(e+1,e+m+1,cmp);
	//初始化 
	init();
	//Kruskal算法核心部分
	int count=0,sum=0;
	for(i=1;i<=m;i++)//开始从小到大枚举每一条边
	{
		//判断一条边的两个顶点是否已经连通
		if(merge(e[i].u,e[i].v))
		{
			count++;
			sum=sum+e[i].w;
		}
		if(count==n-1)//直到选用了n-1条边之后退出循环。 
			break;
	} 
	cout<<sum<<endl;
	return 0;
}

测试样例同上。