42. Trapping Rain Water 及类似题目 407. Trapping Rain Water II 11. Container With Most Water

42. Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example, 
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcosfor contributing this image!

思路1：对每个台阶都寻找左右最大的围墙

对于每一个台阶，都向左和向右寻找最高的那个墙壁，那么最终这个台阶的需水量等于min(maxRight,maxLeft)-height[i]代码如下：

时间复杂度是O(n2)

int trap(vector<int>& height)
{
    int ans = 0;
    int size = height.size();
    for (int i = 1; i < size - 1; i++) {
        int max_left = 0, max_right = 0;
        for (int j = i; j >= 0; j--) { //Search the left part for max bar size
            max_left = max(max_left, height[j]);
        }
        for (int j = i; j < size; j++) { //Search the right part for max bar size
            max_right = max(max_right, height[j]);
        }
        ans += min(max_left, max_right) - height[i];
    }
    return ans;
}

思路2：动态规划方法，建立左右墙壁两个数组

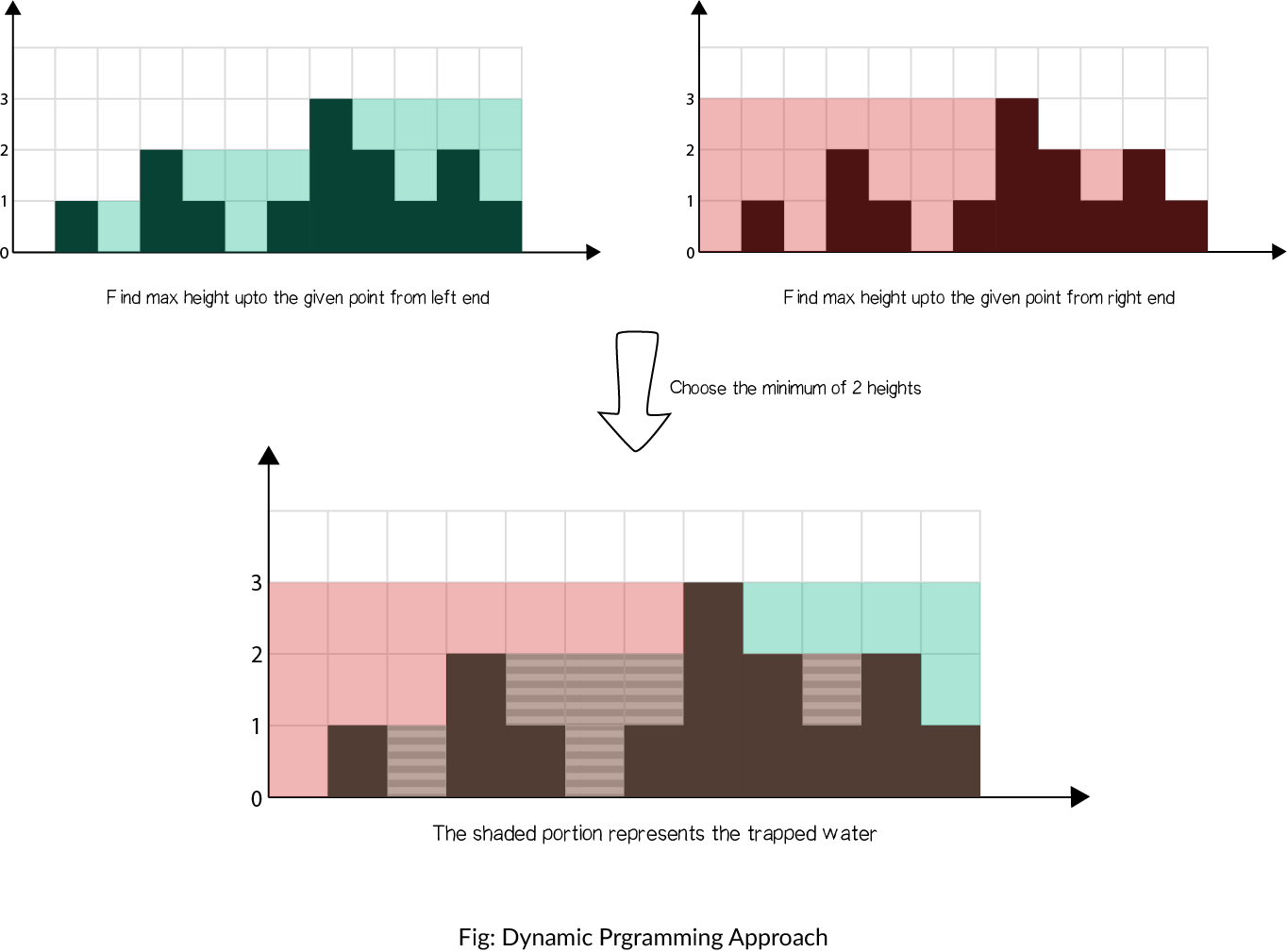
上图的意思是：

分两步考虑，对于一个台阶，只看他左边的最高墙壁，认为右边墙壁和左边墙壁相等，这样每个台阶的储水量都可以求得。而且，左边最高墙壁可以在一次遍历过程中不断更新（只有当前墙壁高于之前的最高墙壁才会更新）；

同样的道理，可以得到只考虑右边墙壁时得到的各台阶的需水量。

一个台阶的实际需水量等于上面两个数组相应位置的最小值。

实际左右分开遍历矩阵时，只需要保存最高墙壁。最后一次遍历时再求需水量

int trap(vector<int>& height)
{
    if(height == null)
        return 0;
    int ans = 0;
    int size = height.size();
    vector<int> left_max(size), right_max(size);
    left_max[0] = height[0];
    for (int i = 1; i < size; i++) {//从左至右遍历，保存当前台阶的左边最大墙壁
        left_max[i] = max(height[i], left_max[i - 1]);
    }
    right_max[size - 1] = height[size - 1];
    for (int i = size - 2; i >= 0; i--) {
//从右至左遍历，保存当前台阶的左边最大墙壁
 right_max[i] = max(height[i], right_max[i + 1]); } for (int i = 1; i < size - 1; i++) {//左右墙壁的最小值-当前台阶的高度是当前台阶的需水量
        ans += min(left_max[i], right_max[i]) - height[i];
    }
    return ans;
}

思路3：使用栈 时间复杂度O(n)，空间复杂度O(n)
可以在一次遍历求得最大需水量
栈为空时，先进栈。
栈不为空时：如果栈顶元素高度大于等于当前高度current，进栈；如果栈顶元素小于当前高度，出栈，计算出栈的元素的蓄水量，找到现在的栈顶和current的最小高度，乘以两个墙壁的距离得到蓄水量，这个蓄水量是栈顶元素做墙的蓄水量。然后继续比较current和栈顶，如果还是满足current>栈顶，继续重复上述操作。这种蓄水方式实际上是一层一层的注水。（这个可以实现的原因是，栈顶的下面的高度一定大于等于上面的值）
当前蓄水完成之后（这些节点的蓄水量一定是全部加完的），再将current进栈，重复外层循环。

int trap(vector<int>& height)
{
    int ans = 0, current = 0;
    stack<int> st;
    while (current < height.size()) {
        while (!st.empty() && height[current] > height[st.top()]) {
            int top = st.top();
            st.pop();
            if (st.empty())
                break;
            int distance = current - st.top() - 1;
            int bounded_height = min(height[current], height[st.top()]) - height[top];
            ans += distance * bounded_height;
        }
        st.push(current++);
    }
    return ans;
}

思路4：使用双指针
这个方法较难想到：
left。right分别在两端，分别保存左右最大值，如果左墙壁最大值小于右墙壁最大值，那么左指针当前台阶的蓄水量由左墙壁决定，这个时候更新左墙壁（因为下一个左墙壁可能还小与右墙壁）。
相反，如果左墙壁最大值大于等于右墙壁最大值，那么右指针当前台阶的蓄水量由右墙壁决定，这个时候更新右墙壁（因为下一个右墙壁可能还小与左墙壁）。
Time complexity: O(n)O(n). Single iteration of O(n)O(n).
Space complexity: O(1)O(1) extra space. Only constant space required for \text{left}left, \text{right}right, left_maxleft_max and right_maxright_max.

int trap(vector<int>& height)
{
    int left = 0, right = height.size() - 1;
    int ans = 0;
    int left_max = 0, right_max = 0;
    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
            ++left;
        }
        else {
            height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
            --right;
        }
    }
    return ans;
}

11. Container With Most Water


Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.


Note: You may not slant the container and n is at least 2.


寻找两条线，他们围成得水池蓄水最多


两个指针分别从左和右向中间逼近。每次计算水池大小（与全局变量比较）。向中间逼近时，只有遇到更高得柱子，才考虑更新水池大小。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n=height.size();
        int areamax=0;
        int i=0,j=n-1;
        while(i<j)
        {
            int hmin=min(height[i],height[j]);
            areamax=max(areamax,(j-i)*hmin);
        while(height[i]<=hmin&&i<j) {
                ++i;
            }
            while(height[j]<=hmin&&i<j) {
                j--;
            }
        }
        return areamax;
    }
};

Leetcode 407. Trapping Rain Water II 收集雨水2 解题报告 使用优先级队列，用pair<int,int> 将矩阵坐标转换成一维值

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        typedef pair<int,int> cell;
        priority_queue<cell, vector<cell>, greater<cell>> q;
        int m = heightMap.size();
        if (m == 0) return 0;
        int n = heightMap[0].size();
        vector<int> visited(m*n, false);
        
        for (int i = 0; i < m; ++i)
        for (int j = 0; j < n; ++j) {
            if (i == 0 || i == m-1 || j == 0  || j == n-1) {
                if (!visited[i*n+j])
                    q.push(cell(heightMap[i][j], i*n+j));
                visited[i*n+j] = true;
            }
        }
        
        int dir[4][2] = {{0,1}, {0, -1}, {1, 0}, {-1, 0}};
        int ans = 0;
        while(!q.empty()) {
            cell c = q.top();
            q.pop();
            int i = c.second/n, j = c.second%n;
            
            for (int r = 0; r < 4; ++r) {
                int ii = i+dir[r][0], jj = j+dir[r][1];
                if (ii < 0 || ii >= m || jj < 0 || jj >= n || visited[ii*n+jj])
                    continue;
                ans += max(0, c.first - heightMap[ii][jj]);
                q.push(cell(max(c.first, heightMap[ii][jj]), ii*n+jj));
                visited[ii*n+jj] = true;
            }
        }
        return ans;
    }
};