Convex Optimization: 2 Convex sets

本篇为凸优化的课程笔记。

Affine set 仿射集

过两个点 $x_1,x_2$ 的直线上所有点形成仿射集。

这个例子可以玩味一下：线性方程组 { x ∣ A x = b } \{x|Ax=b\} {x∣Ax=b} 的解集是仿射集，证明如下：
$$\begin{array}{rl}A{x}_1& =b,A{x}_2=b\\ Ax& =A(\theta x_1+(1-\theta )x_2)\\ & =\theta A{x}_1+(1-\theta )A{x}_2\\ & =\theta b+(1-\theta )b=b\end{array}$$

Convex set 凸集

凸集则是两个点之间的线段形成的集合。

Convex combination and convex hull 凸组合与凸包

凸组合为点的线性组合，其中每个参数要求大于等于零，且参数和为1. 集合 $S$ 的凸包则为 $S$ 中所有点的凸组合。

Convex cone 凸锥

凸锥组合类似凸组合，不同之处在于参数的和没有等于 1 这一限制，但是每个参数仍要大于等于零。凸锥则为集合中所有点的凸锥组合形成的集合。

Hyperplanes and halfspaces 超平面与半空间

超平面既是仿射集又是凸集；半空间只是凸集。

Euclidean balls and ellipsoids 欧几里得球和椭球

欧几里得球是距离中心点的二范数小于 $r$ 的点集，$r$ 是该球的半径。椭球也有相应的表示。

需要注意的是在椭球的第一种表示中 { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \{x|(x-x_c)^TP^{-1}(x-x_c)\le1\} {x∣(x−xc​)TP−1(x−xc​)≤1} 中的 $P$ 和集合是一一对应的，也就是说相同集合对应的矩阵 $P$ 是唯一的，此处 $P$ 是一个对称的正定矩阵。

而在第二种表示中 { x c + A u ∣ ∥ u ∥ 2 ≤ 1 } \{x_c+Au|\|u\|_2\le 1\} {xc​+Au∣∥u∥2​≤1}，此处的矩阵 $A$ 不唯一，假如把 $A$ 换成 $AQ$，其中 $Q$ 是一个正交矩阵，那么这个集合仍然不变，因为相当于是对 $u$ 先做了一下旋转。而假如限定矩阵 $A$ 必须是一个对称正定矩阵的话，$A$ 就变成唯一的了（证明方法是对 $A$ 进行奇异值分解）。

Norm balls and norm cones 范数球与范数锥

范数是一个函数，其满足三个条件：

1. 非负性， 只在 $x=0$ 的时候结果才是零
2. 齐次性
3. 三角不等式

欧几里得范数锥也叫做二阶锥。范数球和范数锥都是凸的。

Polyhedra 多面体

Positive semidefinite cone 半正定锥

Operations that preserve convexity 保持凸性的操作

Intersection 取交

凸集的交集仍是凸集，PPT给的这个例子很妙，见板书里的证明。

Affine function 仿射函数

仿射函数更加一般的说法叫做线性函数。一个凸集经过仿射函数的变换后仍是凸集，反过来也是一样的，凸集经过逆变换之后仍是凸集。注意有可能实际方程的逆变换并不存在，但是凸集经过逆变换之后仍是凸集的这个关系是存在的。

仿射函数的例子有：缩放，平移，投影。

还有双曲锥（hyperbolic cone）：

（？什么是双曲锥）

Perspective and linear-fractional function 透视函数与分式线性函数

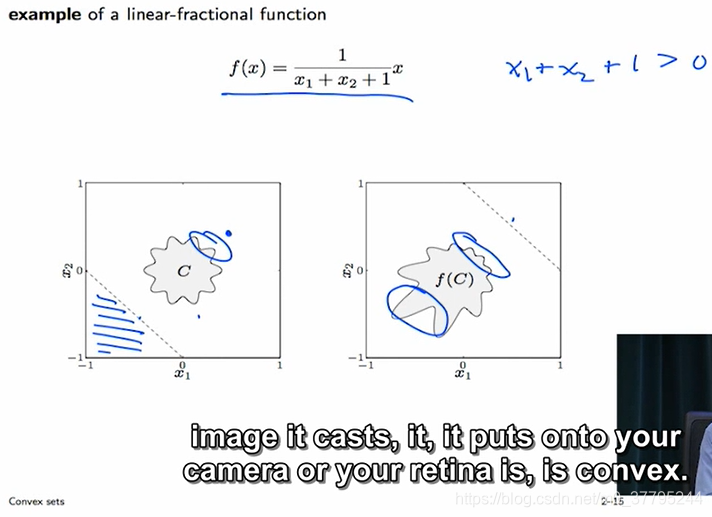
Generalized inequalities 推广的不等式

一个凸锥 $K\subseteq {\mathcal{R}}^n$，当它满足以下三个条件时，被称作是一个真锥（proper cone）：

1. $K$ 是闭的（closed），即包含边界
2. $K$ 是实在的（solid）， 即其内部是非空的，比如一条射线是一个锥，但是这个射线内部是空的（点都在边界上）
3. $K$ 是 pointed 的，意思是不包含直线，比如说一条直线（双向延申）是一个锥，但不是一个真锥，也就是说真锥意味着是单向延申的。

举几个栗子：

• 非负象限： K = R + n = { x ∈ R n ∣ x i ≥ 0 , i = 1 , . . . , n } K=\mathcal{R}_+^n=\{x\in\mathcal{R}^n|x_i\ge 0,i=1,...,n\} K=R+n​={x∈Rn∣xi​≥0,i=1,...,n}
• 半正定锥 $K={\mathcal{S}}_{+}^n$
• $[0,1]$ 上的非负多项式：

K = { x ∈ R n ∣ x 1 + x 2 t + x 3 t 2 + ⋯ + x n t n − 1 ≥ 0  for  t ∈ [ 0 , 1 ] } K=\{x\in\mathcal{R}^n|x_1+x_2t+x_3t^2+\cdots+x_nt^{n-1}\ge 0\text{ for }t\in[0,1]\} K={x∈Rn∣x1​+x2​t+x3​t2+⋯+xn​tn−1≥0 for t∈[0,1]}

generalized inequality 推广不等式：

定义一个真锥 $K$，则：

$$x{⪯}_{K}y⟺y-x\in K,x{\prec }_{K}y⟺y-x\in \mathbf{i}\mathbf{n}\mathbf{t}K$$

即 $x$ 在真锥 $K$ 范围内小于等于 $y$，则说明其差值在真锥范围内；假如是严格小于，则其差值在真锥内部的点中（就是说不在边界上，$\mathbf{i}\mathbf{n}\mathbf{t}$ 表示 interitor）

举几个例子：

• 每个元素的不等式（$K={\mathcal{R}}_{+}^n$，即 $K$ 是非负实数），则：

$$x{⪯}_{{\mathcal{R}}_{+}^n}y⟺x_i\le y_i,i=1,...,n$$

• 矩阵不等式（$K={\mathcal{S}}_{+}^n$）

$$X{⪯}_{S_{+}^n}Y⟺Y-X\text{是半正定的}$$

这两种类型很常见，所以有时会扔掉下标 $K$

性质：${⪯}_K$ 的性质很多和 $\mathcal{R}$ 上 $\le$ 的性质类似，比如：

$$x{⪯}_{K}y,u{⪯}_{K}v⟹x+u{⪯}_{K}y+v$$

Minimum and minimal elements

${⪯}_K$ 并不是一个全序的（linear/total ordering），可以有 $x{⋠}_{K}y$ 并且 $y{⋠}_{K}x$，也就是说这两个元素是不可比较的（incomparable）

比如说在 $K={\mathcal{R}}_{+}^2$ 上：

$$\left[\begin{array}{c}2\\ 1\end{array}\right]⋠\left[\begin{array}{c}1\\ 2\end{array}\right]\text{并且}\left[\begin{array}{c}2\\ 1\end{array}\right]⋡\left[\begin{array}{c}1\\ 2\end{array}\right]$$

也就是说这两个向量是不可比较的。

由此引出了很有趣的概念，在此意义下，最小值有两个概念：

$x\in S$ 在 ${⪯}_K$ 上是 the minimum element 时，

$$y\in S⟹x{⪯}_{K}y$$

$x\in S$ 在 ${⪯}_K$ 上是 a minimal element 时，

$$y\in S,y{⪯}_{K}x⟹y=x$$

比如 $K={\mathcal{R}}_{+}^2$ ，

minimum 是唯一的，并且有可能不存在，根据定义 $S_1$ 中任何一个点都要和 $x_1$ 能够比较，并且 $x_1$ 要小于等于他们，此时 $x_1$ 为 the minimum

minimal 是不唯一的，意思是假如说 $S_2$ 中存在点 $y$ 是可以和 $x_2$ 相比较，并且 $y$ 小于 $x_2$，那么 $y$ 一定等于 $x_2$，此时 $x_2$ 是一个 minimal element,，图中 $S_2$ 左下角边上所有的点都是 minimal element

两种类型的判断方法：

• minimum：过该点画一个锥 $K$，保证集合 $S$ 中的点全在锥中
• minimal：过该点画一个反向锥，保证集合 $S$ 中只有一个点（也就是该点）在这个反向锥中

Separating hyperplane theorem 分离超平面定理

Supporting hyperplane theorem 支撑超平面定理

Dual cones and generalized inequalities 对偶锥以及推广不等式

Minimum and minimal elements via dual inequalities

optimal production frontier