逻辑回归算法

引言

逻辑回归算法的名字里虽然带有“回归”二字，但实际上逻辑回归算法是用来解决分类问题的算法。线性回归和逻辑回归相当于一对“孪生兄弟”，本文将从二分类入手，介绍逻辑回归算法的预测函数、损失函数（代价函数）和梯度下降算法公式，小伙伴们可以不断联想线性回归与逻辑回归的区别与联系。

一、逻辑回归算法的原理

假设有一场球赛，我们有两支球队的所有出场球员信息、历史交锋成绩、比赛时间、主客场、裁判和天气等信息，根据这些信息预测球队的输赢。假设比赛结果记为y，赢球标记为1，输球标记为0，这就是一个典型的二元分类问题，可以用逻辑回归算法来解决。

从这个例子里可以看出，逻辑回归算法的输出y ∈ { 0 , 1 } 是个离散值，这是与线性回归算法的最大区别。

1.1 预测函数

需要找出一个预测函数模型，使其值输出在[ 0 , 1 ]之间。然后选择一个基准值，如0.5，如果算出来的预测值大于0.5，就认为其预测值为1，反之则其预测值为0。我们选择g(z) = $\frac{1}{1+e^{-z}}$来作为预测函数。函数g ( z ) 称为Sigmoid函数，也称为Logistic函数。图像如下：

当z=0时，g(z)=0.5。
当z>0时，g(z)>0.5，当z越来越大时，g(z)无限接近于1。
当z<0时，g(z)<0.5，当z越来越小时，g(z)无限接近0。
对二分类来说，这是一个非黑即白的世界。

这正是我们想要的针对二元分类算法的预测函数。问题来了，怎样把输入特征和预测函数结合起来呢？


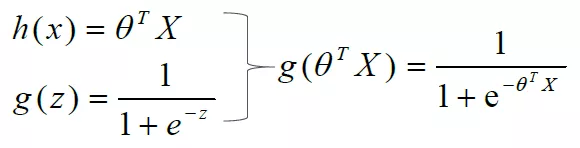
总结起来就是：

举个栗子：

那么

这个看起来是不是很像我们中学学过的线性规划，没错，线性规划是已知了约束条件（决策边界）和目标函数，让我们寻找最优解的过程，而逻辑回归则是寻找决策边界的过程，。

1.2 损失函数（代价函数）

我们不能使用线性回归模型的损失函数来推导逻辑回归的损失函数，因为那样的损失函数太复杂，最终很可能会导致无法通过迭代找到损失函数值最小的点。为了容易地求出损失函数的最小值，我们分成y=1和y=0两种情况分别考虑其预测函数值与真实值的误差。我们先考虑最简单的情况，即计算某一个样本(x,y)的预测值与真实值的误差，损失函数如下：

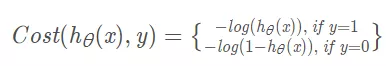
其中，$h_{\theta }(x)$表示预测为1的概率，这样不管实际是y=0还是y=1，损失函数的值都是最小。虽然这样可以表示，但是还要分类讨论，还是太麻烦，于是，我们引入了下面这个函数。

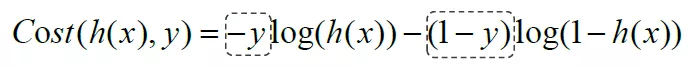
嘿嘿嘿，是不是瞬间丝滑了很多，这样，就不用分类讨论了。
我们简化一下损失函数，得到：

由线性回归的章节我们知道，我们的目标是找到某θ使损失函数最小，即$mi{n}_{\theta }J(\theta )$，实现的方法也是使用梯度下降算法，即${\theta }_j={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}$。那么关键就是如何求损失函数对θ的梯度$\frac{\partial J(\theta )}{\partial {\theta }_j}$。推导过程如下（需具备一定的高等数学基础）：

二、案例实现

接下来我们通过分别手动梯度下降法和调用sklearn接口实现逻辑回归。

2.1 梯度下降法实现线性逻辑回归

1. 首先导入需要用到的库并导入数据集（本地数据）。

import numpy as np
import matplotlib.pyplot as plt

# 读取数据
data = np.genfromtxt("LR-testSet.csv",delimiter=",")
data

# 特征：选择前两列
x_data = data[:,:-1]
# 标签：y
y_data = data[:,-1]

2. 将数据集可视化展示。

"""
可视化
- y_data为0是一个类别，圆
- y_data为1是一个类型，叉

实现：
- 构建x1,x2
"""
def plot_logi():
    # 初始化列表
    x_0 = []
    y_0 = []
    x_1 = []
    y_1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        # 取类别为0的数据
        if y_data[i] == 0:
            # 将特征1添加到x_0中
            x_0.append(x_data[i,0])
            # 将特征2添加到y_0中
            y_0.append(x_data[i,1])
        else:
            # 将特征1添加到x_1中
            x_1.append(x_data[i,0])
            # 将特征2添加到y_1中
            y_1.append(x_data[i,1])
    
    # 画图
    plt.scatter(x_0,y_0,c="skyblue",marker="o",label="class0")
    plt.scatter(x_1,y_1,c="red",marker="x",label="class1")    
    plt.legend()
    
plot_logi()
plt.show()

如图所示：

3. 对数据进行处理，划分为特征和标签，并考虑到常数项，给X添加一列全为1的数据。

# 特征：选择前两列
x_data = data[:,:-1]
# 标签：y
y_data = data[:,-1]

# θ^T*X  给X添加一列全为1的数据
X_data = np.concatenate((np.ones((len(x_data),1)),x_data),axis=1)

4. 定义sigmoid函数、损失函数以及梯度下降求解函数。

# 定义sigmoid函数  x=θ^T*X
def sigmoid_(x):
    return 1/(1+np.exp(-x))


# 定义损失函数 xMat:x_data矩阵  yMat：y_data矩阵  ws：参数向量的转置
def cost_(xMat,yMat,ws):
    # 进行相乘
    left = np.multiply(yMat,np.log(sigmoid_(xMat*ws)))
    right = np.multiply(1-yMat,np.log(1-sigmoid_(xMat*ws)))
    
    # 进行求和 除以样本的个数
    return np.sum(left+right)/-(len(xMat))
    

# 定义梯度下降求解θ
def gradAscent(xArr,yArr):
    # 将ndarry类型转为矩阵
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    
    # 初始化学习率
    lr = 0.001
    
    # 初始化迭代次数
    epochs = 10000
    
    # 取出 样本个数m 以及 特征个数n
    m,n = np.shape(xMat)  
    
    # 初始化的θ --> θ^T*xMat   θ0*x0+θ1*x1+θ2*x2  
    ws = np.mat(np.ones((n,1)))
    
    # 初始化损失列表
    costList = [] 
    
    # 迭代
    for i in range(epochs+1):
        # 求导
        # 1.h(x)  100*3 3*1 --> 100*1 -->每个样本都有一个h(x)
        h = sigmoid_(xMat*ws)
        # print(f"xMat shape:{np.shape(xMat)}")
        # print(f"ws shape:{np.shape(ws)}")

        
        # 矩阵乘法：n*m m*1 --> n*1 -->
        # xMat:m*n  3*100   m*1 1*100
        # h-->预测值  (m*1)
        # yMat-->真实值 (m*1)
        ws_grad = xMat.T*(h - yMat.T)/m
        # print(f"xmat.T shape{np.shape(xMat.T)}")
        # print(f"yMat shape{np.shape(h - yMat.T)}")

        # print(np.shape(ws_grad))
        
        # 更新ws-->theta向量
        ws = ws - lr*ws_grad
        
        if i%50 == 0:
            costList.append(cost_(xMat,yMat,ws))
            
    # 返回theta向量ws，以及损失列表
    return ws,costList

5. 训练模型。

# 训练模型
ws,costList = gradAscent(X_data,y_data)
print(ws)

输出参数结果：

[[ 5.43584839]
 [ 0.58587197]
 [-0.78304626]]

6. 将结果可视化。

"""
可视化
- 横轴:x1
- 纵轴:x2
x1*theta1+x2*theta2+theta0=0
x2 = -(x1*theta1+theta0)/theta2
"""
# 绘制点
plot_logi()

# 初始化测试集的数据
x_test = [[-4],[3]]
# 计算分类函数
y_test = -(x_test*ws[1]+ws[0])/ws[2]
# 可视化
plt.plot(x_test,y_test)
plt.show()

如图所示，分类效果还可以。

7.绘制loss曲线。

# 绘制loss曲线
# 生成0,10000
x = np.linspace(0,10000,201)
plt.plot(x,costList)
plt.xlabel("epochs")
plt.ylabel("Cost")
plt.show()

可以看到，经过大约500次迭代后，loss值就趋于稳定了。

2.2 sklearn实现线性逻辑回归

1. 下面介绍第二种方法，用sklearn实现，前面基本都一样，导入库和数据，将数据集可视化。

import numpy as np
import matplotlib.pyplot as plt

# 读取数据
data = np.genfromtxt("LR-testSet.csv",delimiter=",")
data

# 特征：选择前两列
x_data = data[:,:-1]
# 标签：y
y_data = data[:,-1]

def plot_logi():
    # 初始化列表
    x_0 = []
    y_0 = []
    x_1 = []
    y_1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        # 取类别为0的数据
        if y_data[i] == 0:
            # 将特征1添加到x_0中
            x_0.append(x_data[i,0])
            # 将特征2添加到y_0中
            y_0.append(x_data[i,1])
        else:
            # 将特征1添加到x_1中
            x_1.append(x_data[i,0])
            # 将特征2添加到y_1中
            y_1.append(x_data[i,1])
    
    # 画图
    plt.scatter(x_0,y_0,c="skyblue",marker="o",label="class0")
    plt.scatter(x_1,y_1,c="red",marker="x",label="class1")    
    plt.legend()
    
plot_logi()

2. 训练这一个环节相比方法一就简单太多了，两行代码搞定！

# 训练模型
logistic = LogisticRegression()
logistic.fit(x_data,y_data)

# 截距
print(logistic.intercept_)
# theta1 theta2
print(logistic.coef_)

输出结果，截距为θ0=11.386，斜率θ1=0.857，θ2=-1.542：

[11.38607726]
[[ 0.85767013 -1.54232428]]

3.进行可视化展示

# x2 = -(x1*theta1+theta0)/theta2
# 画出散点
plot_logi()
# 画出决策边界
x_test = np.array([[-4],[3]])
y_test = -(x_test*logistic.coef_[0,0]+logistic.intercept_)/logistic.coef_[0,1]
plt.plot(x_test,y_test)
plt.show()

如图，感觉分类效果比上面要好一点（这不是废话吗，人家可是sklearn哈哈哈）：

4. 进行评分.

print(logistic.score(x_data,y_data))

得到结果为0.95，对于线性分类模型，这个结果已经非常不错了。OK，收工~

小伙伴，你学会了吗？扫码关注公众号，在后台回复“逻辑回归”即可获取数据集和源代码。