SVM支持向量机-——希尔伯特空间解释

转载(https://zhuanlan.zhihu.com/p/88946250)
转载

量子力学第一条基本原理：微观系统的状态用希尔伯特空间的矢量 描写，而 称为态矢量或态函数。

量子力学第二条基本原理：微观系统的物理量用希尔伯特空间的线性厄米算符表示，物理量的可能取值是相应算符的本征值。

量子力学的其他几个基本原理就不赘述了。

学习一个理论必须先学习它的基本原理，因为这个理论之后的一切都要从基本原理出发，一步一步推导出来。

通过上面两个基本原理，我们看到了要想理解量子力学，必须理解什么是态矢量 ，要想理解什么是态矢量 ，必须理解什么是希尔伯特空间。可见理解希尔伯特空间的定义是多么重要，那么下面就进入正题，直接定义一下什么是希尔伯特空间：

一、线性空间

线性空间的定义是：

设V是一个非空集合，R一个数域(可以是实数也可以是复数)。如果对于任意两个元素α, β∈V，总有唯一的一 个元素γ∈V与之对应，称γ为α与β的和(简称加法运算)，记作γ=α+β。若对于任一数λ∈R与任一元素α∈V，总有唯一的元素δ∈V与之对应，称d为数λ与α的积(简称数乘运算)，记作δ=λα。

加法和数乘必须满足：

1 加法交换律: α+β=β+α;

2 加法结合律: (α+β)+y=α+(β+y);

3 零元素:存在O∈V,对任一向量α, 有α+O= α;

4 负元素:对任一元素α∈V, 存在β∈V,有α+β=O, 记β=-α;

5 1 α=α;

6 数乘结合律:k(lα)=(kl)α;

7 数乘对加法的分配律: k(α+β)= kα +kβ;

8 数量加法对数乘的分配律: (k+l)α= kα+lα。

简单来说，线性空间就是定义了加法和数乘的非空集合。

二、内积空间

对于一个线性空间中的任意两个矢量 和 , 都有一个数域上的数c与之对应, 记为

, 并且该对应关系满足内积运算的定义。

而内积运算的定义为：对于一个线性空间中的任意三个矢量 和一个复数域上的数 , 满足下列关系的运算关系：

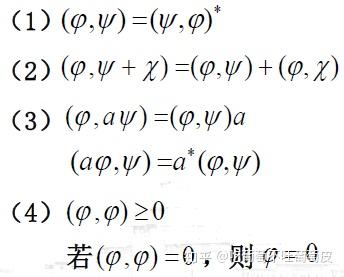
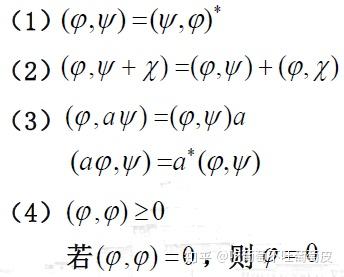
则这样的运算关系叫内积运算。

简单来说，内积空间就是定义了内积的线性空间。

三、Cauchy序列

Cauchy序列: 在某个数域的线性空间中, 把线性空间中的向量的“长度”（或者向量自己与自己的内积对应的实数）从小到大排列起来，并依次用正整数m标记，形成一个序列 。则对于任意小的正实数, 都存在一个正整数N, 当m, n>N时, 有 , 其中 是线性空间中的矢量, 满足这条性质的序列 就是Cauchy序列。

简单来说，一个柯西列是指一个这样一个序列，它的元素随着序数的增加而愈发靠近; 更加严格的理解: 可以通过选择有限个点去掉, 使得剩下的点的最大距离小于任意正整数。

四、空间的完备性

空间完备性的定义: 对于一个内积空间, 其任一柯希序列的极限也属于这个空间时，则这个性质叫空间的完备性。

五、希尔伯特空间

希尔伯特空间就是完备的内积空间。

定义完毕。

通俗解释：

希尔伯特空间是指完备正交的线性空间，可以是无穷维，也可以是有限维。而日常三维可以称为三维完备正交线性空间。是不是很像？

要明白希尔伯特空间，先从数学物理角度的维度说起。所谓维度，不单单指空间维度和时间，其最基本的概念叫做，描述一个状态的坐标数。因为是正交的，所以是独立坐标数。（正交下文再提）在空间中，描述一个东西的位置状态，需要三个独立坐标，所以有空间三维。如果要描述物体的运动状态，除了空间三维，还需要它在三个空间方向的动量坐标，即共6个独立坐标，构成了一个六维空间，物理上称之为相空间（对，就是你力学书上那个！）。希尔伯特空间就是由若干个（可以是任意数量）独立坐标构成的抽象空间。量子力学里，就是本征矢构成的。

同样用三维空间类比，为了描述三维，我们设定了xyz三个坐标构成一个坐标系，单位坐标是1，这些都是中学物理的内容。在数学上，我们称xyz的单位坐标为基矢量，通过对这三个基矢量的平移，我们能获得一个完整的三维空间。可以说，空间（线性的）都是由基矢量的平移构成的。

希尔伯特空间也不例外，但特别的是，希尔伯特空间的基矢不是定长的，各个基矢的大小不一定是一样的。它的基矢可以是函数！数学上，函数是可以作为广义坐标的，为什么我也不知道，分析数学没学好。。。

综上，希尔伯特空间就是由若干个函数作为独立坐标构成的抽象空间。

最后说说比较细节的东西，一个是正交完备，一个是线性。

所谓正交，很好理解，就是三维中的垂直。我们可以说，直角坐标系构成的空间是一个正交空间，因为xyz三个坐标基矢量相互垂直/正交。当然，没有人能想象高维空间的垂直，改称为正交，其更本质的含义是相互独立。类比于日常三维，就是当一个矢量在x轴方向上延长，它在yz轴上的坐标可以是不发生变化的，相互间互不影响。相互独立可以用内积是否为0判断，在二维三维里，内积就是矢量乘法，中学里学过，相互垂直的矢量，数量积为0。

然后是完备，完备就是说这个空间没有洞，也就是我们所要描述的这类状态的所有可能值都被这个空间包含了。如果这个空间有洞，那洞里的那个状态，我们就不能描述了。日常三维就是个完备的空间。想象一下，我们愉快的生活在一张纸上的世界，以我们2维的视角，这个世界是完备的，所有东西的位置都是可描述的。某一天，一个不可描述的大能拿它沾了口水的手指在纸上戳了个洞。这个洞对我们而言就变成了未知。可能你的小芳本来在洞的那个位置，在那瞬间，emmmm。。。你的小芳不见了，你甚至不知道她在哪里，就像她突然消失了。

最后讲讲线性。1+1=2，这就是线性。线性就是指不同的量之间满足加法规则（减法也行，减法是加法的逆运算）。日常三维是线性的，因为如果你往东先走5m，再走5m，总共走了5+5=10m。绝大部分人能接触到的空间概念，都是线性的，日常三维可以称为三维完备正交线性空间。（所以理工科都要学线性代数，都是泪啊）