0、前言
LDA是两个常用模型的简称:Linear Discriminant Analiysis 和Latent Dirichlet Allocation.
LDA(Latent Dirichlet Allocation)在文本建模中类似于SVD,PLSA等模型,可以用于浅层语义分析,在文本语义分析中是一个很有用的模型.
这个模型涉及到Gamma函数,Dirichlet分布(狄利克雷分布),Dirichlet-Multinomial共轭,Gibbs Sampling,Variational Inference,贝叶斯文本建模,PLSA建模,以及LDA文本建模.
1、Gamma函数
形式:
gamma函数性质:
并且Γ函数的计算有以下规律:
从二项分布到Gamma分布:
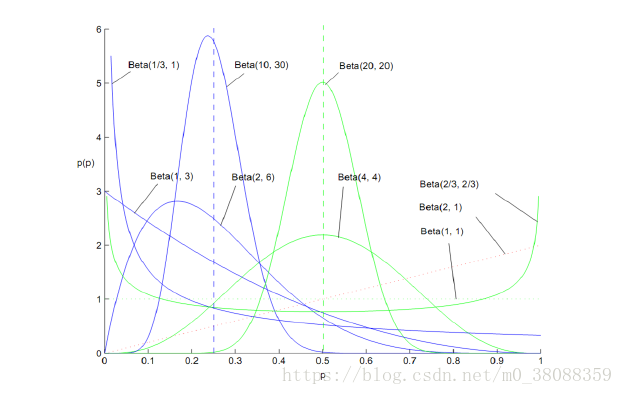
2、Beta分布
引入一个典例:
不是一般性:
其中x属于0-1之间的数。此时把题目所需求的k值带入公式即可求出来概率的函数。
3、Beta-Binomial 共轭
再引入一个典例:
现在问的是一个后验概率,也可以理解为条件概率。
上图中横轴为我们要描述的概率p,纵轴为概率的概率。
虽然我们的概率是未知的,但是随着我们实验次数增加,先验知识的增加,我们对概率的分布进行建模,进而用分布的期望值对概率进行预测。
4、Dirichlet-Multinomial 共轭
当概率分布是多项式分布的时候就要用狄利克雷分布。也就是将Beta分布扩展到多项分布。
继上面引入一个典例:
我们取:
同样对于先验知识越多,概率的估计就越准确。
如果再满足这样的先验知识:
5、Beta与Dirichlet分布的一个性质
如果概率p服从Beta分布,则满足:
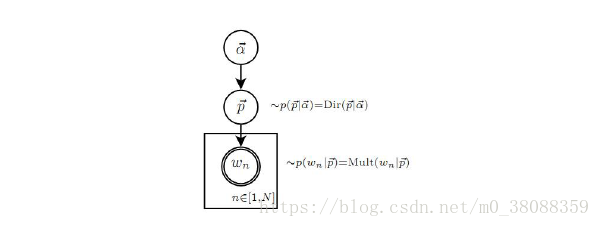
6、Unigram Model
在这里最重要的一个参数固然就是概率pk,贝叶斯统计学派认为一切参数都是随机变量,包括上帝选择的这枚骰子也是随机的,所以以上模型中骰子的概率p(向量)不是唯一固定的。所以再引入了一下过程。
这个先验分布是用来确定每个骰子被使用的概率的,而可以发现此处先验概率有很多种选择,实际上就是计算一个多项分布的概率,所以对先验分布比较好的选择就是多项分布对应的共轭分布,即狄利克雷分布。
Unigram Model 的概率图模型:
由参数p(向量,因为多个概率)的后验分布的期望来参数p的估计。由上面小节提到的p的后验分布为狄利克雷分布,于是:
7、Topic Model 和 PLSA
在这里先提一下—LSA 主题模型:
LSA为Latent Semantic Analysis简称。LSA通过SVD分解等处理,消除同义词、多义词影响,提高后续处理的精度。是一种简单的主题模型。
奇异值分解公式如下:
原理:
(1)分析文档集合,建立词汇-文本矩阵。
(2)对词汇-文本矩阵进行奇异值分解。
(3)对SVD分解后的矩阵进行降维
(4)使用降维后的矩阵构建潜在语义空间
LSA详细流程:
LSA初始矩阵的生成:
(1)生成词汇库(以英文文本为例)
a从文本中过滤非英文字母字符;
b过滤禁用词;
c相同词根单词归一;
d词汇统计和排序:
e生成词汇库
(2)生成词汇-文本矩阵
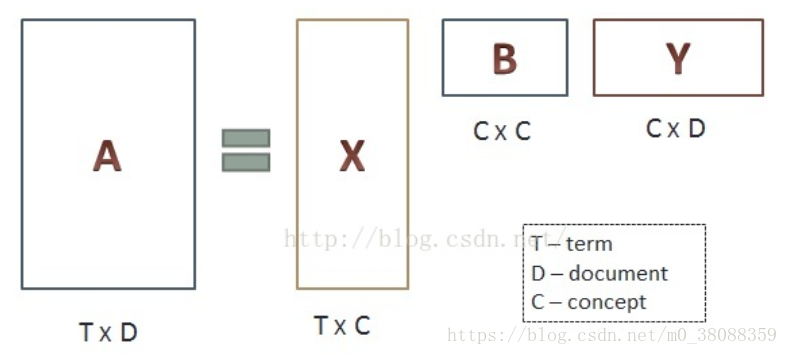
由各索引词在每篇文本中的出现频率生成词汇-文本矩阵 X 该矩阵中(第 i行第 j 列的元素数值aij 表示第 i个索引词在第 j 篇文本中出现的频率或者TF-IDF加权词频)
初始矩阵中每一行对应一个词,每列对应一篇文章,T个词和D篇文章可以表示为T*D的矩阵
(3)奇异值分解
注意:
(1)第一个小矩阵X是对词进行分类的一个结果,它的每一行表示一个词,每一列表示一个语义相近的词类,这一行中每个非零元素表示每个词在每个语义类中的重要性(或者说相关性)
(2)第二个小矩阵B表示词的类和文章的类之间的相关性
(3)矩阵Y是对文本进行分类的一个结果,它的每一行表示一个主题,每一列表示一个文本,这一列每个元素表示这篇文本在不同主题中的相关性
通过SVD矩阵分解我们可以得到文本、词与主题、语义之间的相关性,但是计算出来内容存在负数难以解释。此外可以对LSA得到的文本主题矩阵使用余弦相似度计算文本的相似度,因为在文本主题矩阵中每一列代表了不同的文本,而每一行又代表了不同的主题。(这个时候直接在文本主题矩阵应用聚类算法即可得)。
LSA缺点:
(1)SVD计算非常耗时,对于高纬度矩阵做SVD分解非常困难。
(2)主题模型的数量的选取对于结果的影响非常大,很难选择合适的k值。
(3)LSA模型不是概率模型,缺乏统计基础,结果难以直观的解释。
PLSA Topic Model:
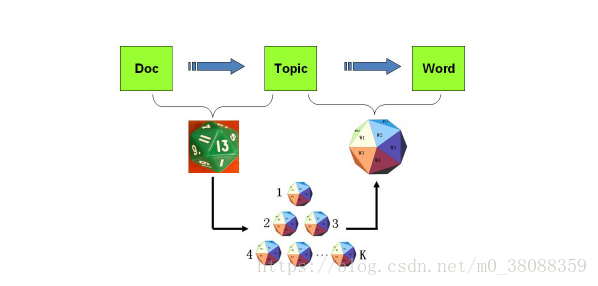
以上Unigram Model模型中的假设看起来过于简单,与人类写文章产生的每一个词的过程差距比较大。在现实当中人类没构思一篇文章往往先确定几个主题,然后通过主题再想出与主题相关的词。而人类之所以能想到这些词,是因为这些词对应的主题下出现的概率很高(但不代表在其他主题当中不出现)。
一篇文章通常由多个主题构成,而每一个主题的大概可以用与该主题相关的频率最高的一些词来描述。
所以引入了一下的过程:
图示化过程如下:
以上公式当中的z就是我们骰子抽取的主题z,而这个z可以理解为一个隐变量。存在隐变量的问题可以用EM模型来求解。(过程分为E步和M步)
PLSA主题模型认为上面骰子抽取的概率是确定的,没有先验分布,而LDA主题模型不认为他是确定的,认为他是一个分布。
8、LDA
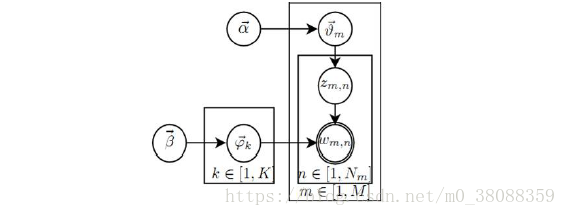
LDA概率图模型如下:
以上参数说明:
定义K-主题数,M-文章数,V-单词数
M篇文章分别为d1,d2…dm,θm表示文章dm的向量,展开为θm=(p1,p2…pk),表示k个主题在这篇文章中的概率分布.
Zm,n表示第m篇文章第n个单词的主题.
φk表示主题为k的词的概率分布.
9、Gibbs Sampling
(1)什么是sampling?
sampling就是以一定的概率分布,看发生什么事件。举一个例子。甲只能E:吃饭、学习、打球,时间T:上午、下午、晚上,天气W:晴朗、刮风、下雨。现在要一个sample,这个sample可以是:打球+下午+晴朗。
我们不知道p(E,T,W),但是,我们知道三件事的conditional distribution。也就是说,p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法,得到联合分布。
首先随便初始化一个组合,i.e. 学习+晚上+刮风,然后依条件概率改变其中的一个变量。具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习-》吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风-》吃饭+上午+刮风。同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
(2)接着以上得到的P(w,z)联合分布,用Gibbs Sampling 算法对这个分布进行采样。因为w是观测到的已知单词向量,只有z主题向量是隐含的变量,所以需要采样的是分布P(z|w)。
10、LDA模型的训练过程以及预测过程










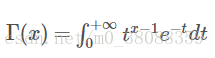

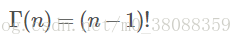




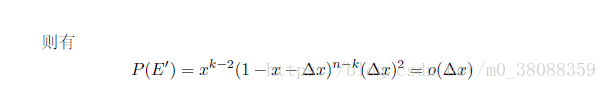


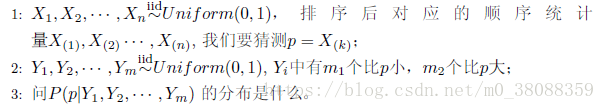



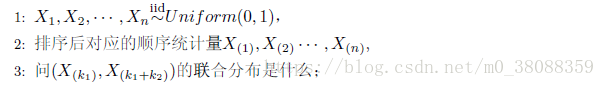
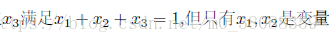





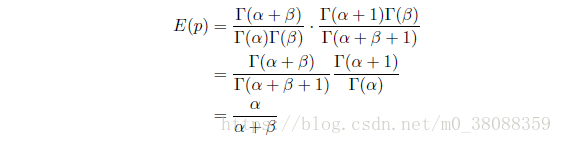




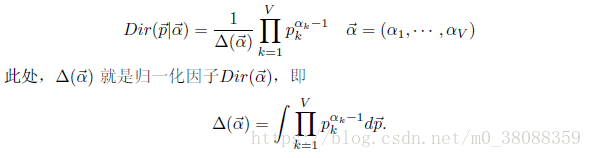

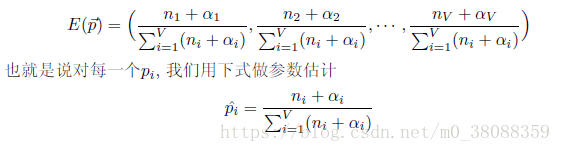



























 701
701











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








