本文详细介绍了Kuhn-Munkras算法，一种解决带权重完全匹配问题的方法。通过4*4矩阵展示了从最大匹配转换到最小成本匹配的过程，包括行和列的最小值调整，以及如何用最少的线覆盖所有零元素。最终，通过实例演示了如何找到匹配组合，实现了完整的匹配解决方案。该算法在优化分配问题中有着广泛应用。
带权重的匈牙利KM算法
Kuhn-Munkras算法为带权重的匈牙利算法
参考视频链接：https://www.bilibili.com/video/BV16K4y1X7Ph?spm_id_from=333.337.search-card.all.click
1.得到4*4的矩阵 从最大matching转换到min cost match问题
 |
 |
2. 每一行减去最小值
每一行减去最小值：
 |
 |
每一列减去最小值：
 |
 |
4.用最少横纵线cover掉所有的0 目前三条线
！！！截止条件：最小线=n 此处n为4，小于4则循环
5. 找到没有覆盖的部分最小值 k=2，没被覆盖部分全部减去2
6.红线交叉地方加上k=2
7.完成第一轮循环
8. 需要四条红线覆盖所有的0，循环终止
 |
 |
 |
 |
 |
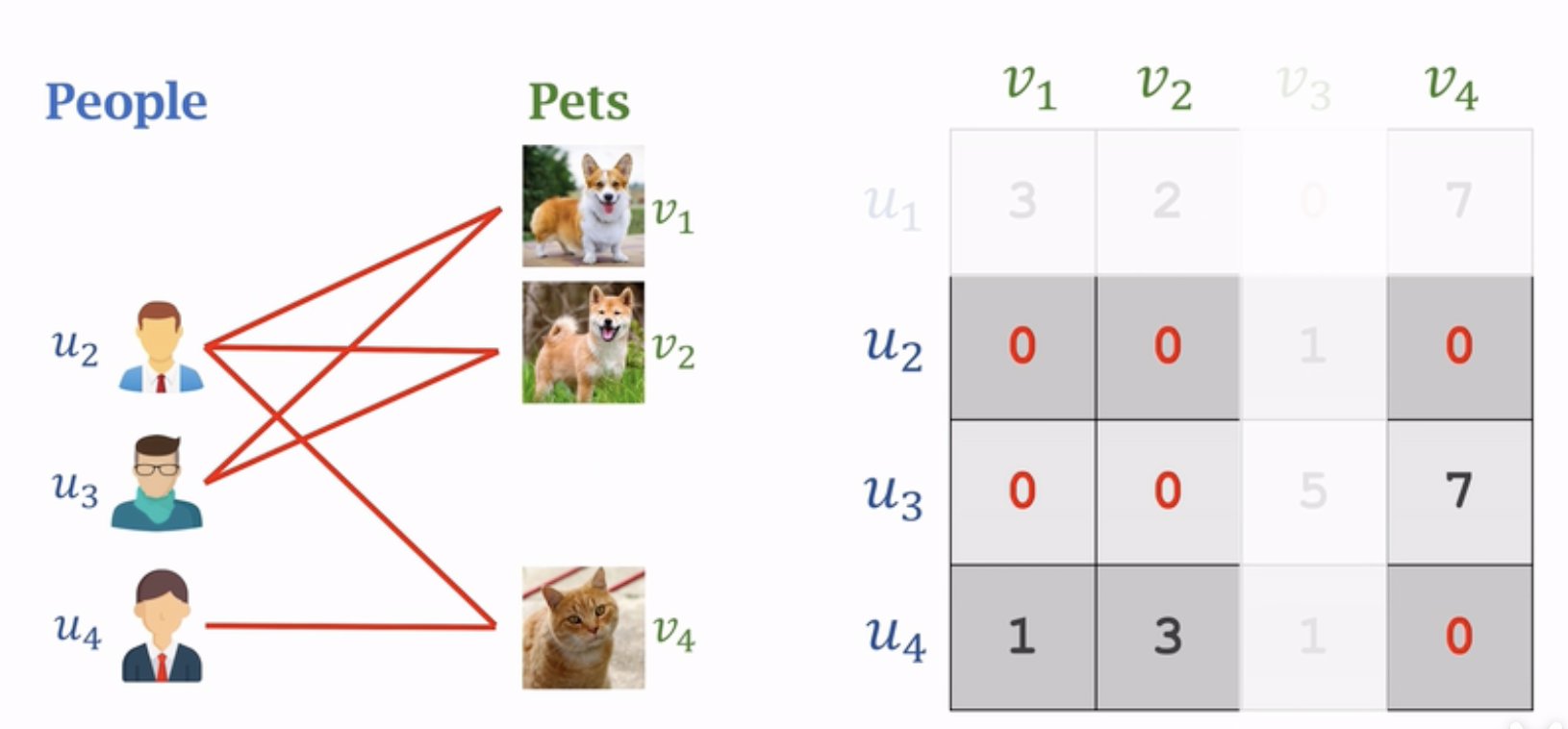
9. 第一行只有一个0保证u1->v3匹配
10.最后一行只有一个0，u4->v2匹配
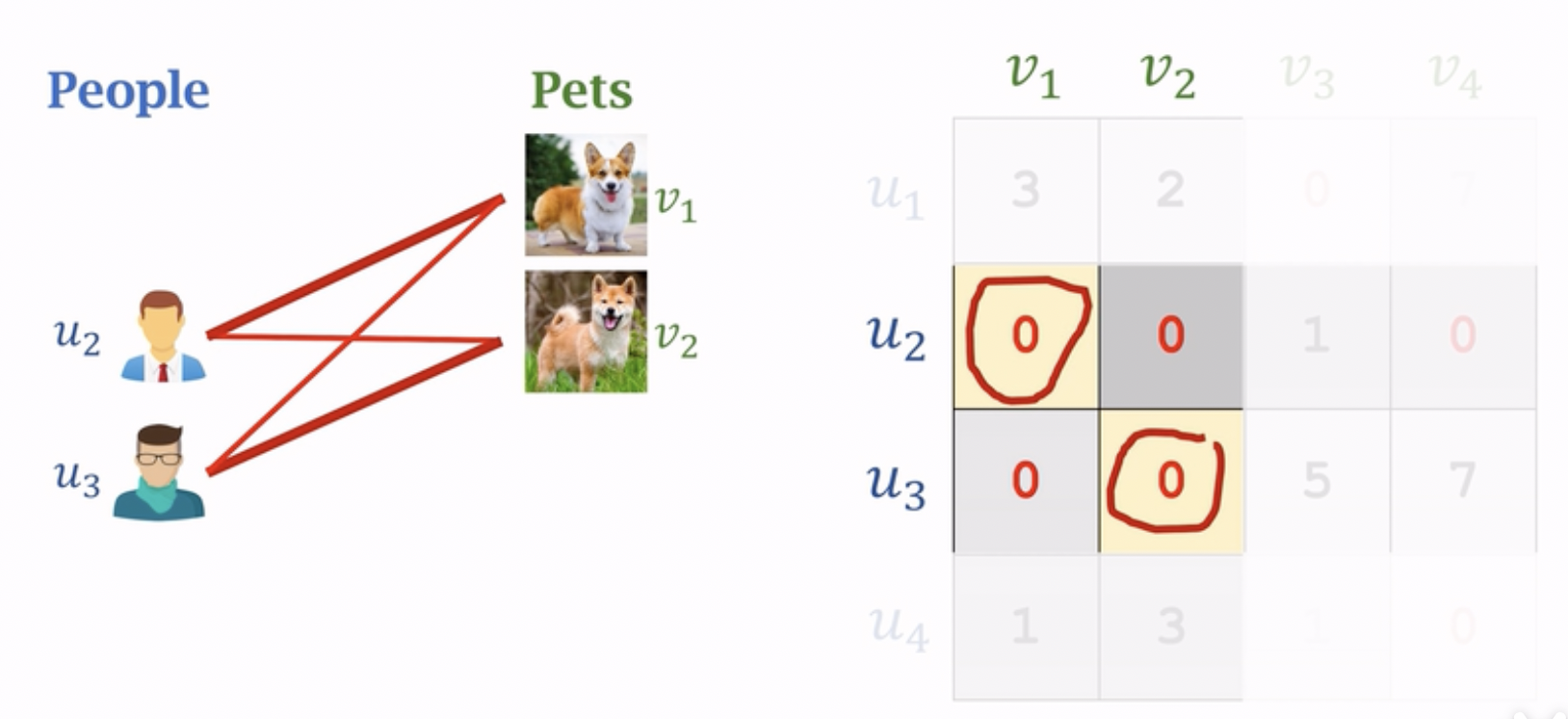
11.第一种匹配方式 u2->v1, u3->v2
 |
 |
 |
12 result
第一种组合方式：
 | 第二种组合方式：
 |
扫一扫
1332
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
