（Gauss-Jordan）高斯消元法求逆矩阵（含C/C++实现代码）

一、问题引出

给定一个 $n\times n$ 的矩阵 $A$ ，我们想求得一个矩阵 $B$ 使得 $|A\times B|$ 即 $A$ 矩阵和 $B$ 矩阵的积矩阵的行列式为 $1$ ，那么这个 $B$ 矩阵就是 $A$ 矩阵的逆矩阵，或者说 $A\times B$ 得到单位矩阵 $E$

二、原理

2.1 矩阵求逆原理

• 我们先构造出一个 $n\times 2n$ 的增广矩阵 $(A,I_n)$
• 然后用高斯消元法将这个增广矩阵化为最简形式 $(I_n,A^{-1})$ ，此时的增广部分就是 $A$ 矩阵的逆矩阵，如果最后简化的左半部分矩阵不是单位矩阵那么说明矩阵 $A$ 不可逆

2.2 矩阵消元原理

• 对于一个矩阵 $A$ ，我们从第 $1$ 行到第 $n$ 行不断选取第 $i$ 列不为 $0$ 的行，然后做一个行变换（交换两行，使得当前的第 $i$ 行的第 $i$ 列不为0）
• 然后将当前的第 $i$ 行做一个初等变换，也就是都除以 $A[i][i]$ 这样的话就能让第 $i$ 行第 $i$ 列变为 $1$
• 将第 $i$ 行下面的所有行的第 $i$ 列全部消掉，此时就构成了一个上三角矩阵
• 此时已经构成了一个阶梯型矩阵，我们再从下往上不断将上半矩阵同理消掉即可

三、举例

我们要求的 $A$ 矩阵如下：
$$\left[\begin{array}{c}211\\ 321\\ 212\end{array}\right]$$

1. 我们构造出增广矩阵：

$$\left[\begin{array}{c}211100\\ 321010\\ 212001\end{array}\right]$$

2. 开始行变换，消除下三角

$$\left[\begin{array}{c}11/21/21/200\\ 01-1-320\\ 001-101\end{array}\right]$$
3. 从下往上消除上三角形

$$\left[\begin{array}{c}1003-1-1\\ 010-421\\ 001-101\end{array}\right]$$

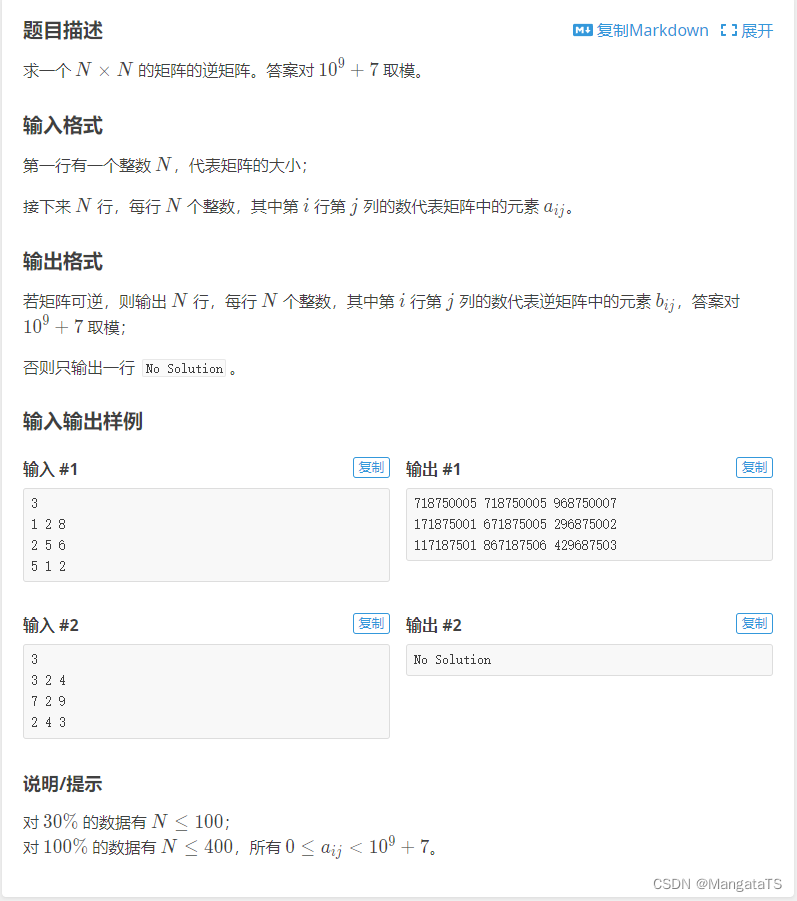
四、题目链接

https://www.luogu.com.cn/problem/P4783

五、代码实现

5.1 整数逆元逆矩阵

对于这个整数逆元逆矩阵，需要注意的一点是模数最好选择一个质数，否则很容易存在逆元不存在的情况，导致求解出来的逆矩阵不正确

#include<bits/stdc++.h>
#define re register
#define il inline
#define ll long long
using namespace std;

il ll read(){
    ll s=0,f=0;char c=getchar();
    while(c<'0'||c>'9') f=(c=='-'),c=getchar();
    while(c>='0'&&c<='9') s=(s<<3)+(s<<1)+(c^'0'),c=getchar();
    return f?-s:s;
}

const int N=405,mod=1e9+7;
int n;
ll a[N][N<<1];
il ll qpow(ll x,ll k){
	ll ans=1;
	while(k){
		if(k&1) ans=ans*x%mod;
		x=x*x%mod;
		k>>=1;
	}
	return ans%mod;
}

il void Gauss_j(){	
	for(re int i=1,r;i<=n;++i){
		r=i;
		for(re int j=i+1;j<=n;++j)
			if(a[j][i]>a[r][i]) r=j;
		if(r!=i) swap(a[i],a[r]);
		if(!a[i][i]){puts("No Solution");return;}
		
		int kk=qpow(a[i][i],mod-2);	//求逆元 
		for(re int k=1;k<=n;++k){
			if(k==i) continue;
			int p=a[k][i]*kk%mod;
			for(re int j=i;j<=(n<<1);++j) 
				a[k][j]=((a[k][j]-p*a[i][j])%mod+mod)%mod;
		} 
		
		for(re int j=1;j<=(n<<1);++j) a[i][j]=(a[i][j]*kk%mod);
		//更新当前行 如果放在最后要再求一次逆元,不如直接放在这里  
	}	
	
	for(re int i=1;i<=n;++i){
		for(re int j=n+1;j<(n<<1);++j) printf("%lld ",a[i][j]);
		printf("%lld\n",a[i][n<<1]);
	}
}
int main(){
	n=read();
	for(re int i=1;i<=n;++i)
		for(re int j=1;j<=n;++j)
			a[i][j]=read(),a[i][i+n]=1;
	
	Gauss_j();
    return 0;
}

5.2 浮点逆矩阵

对于浮点逆矩阵那么直接用高斯消元的方式做就好了

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 26
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f
#define EPS 0.00001

const int N = 1e2+10;
ll n;
double a[N][N],b[N][N];

void output(double a[N][N],double b[N][N]){
	//调试输出
	cout<<"调试输出：左边为A矩阵，右边为B矩阵"<<endl;
	for(int i = 1;i <= n; ++i) {
		for(int j = 1;j <= n; ++j) {
			cout<<a[i][j]<<"\t";
		}
		for(int j = 1;j <= n; ++j) {
			cout<<b[i][j]<<"\t\n"[j == n];
		}
	}
}


void guss(){
	for(ll i = 1;i <= n; ++i) {//枚举当前处理到第几列
		for(ll j = i;j <= n; ++j) {//找到一个第i列不为空的行
			if(fabs(a[i][i]) > EPS) {
				for(ll k = i;k <= n; ++k) //交换i,j行
					swap(a[i][k],a[j][k]);
				break;
			}
		}
		if(fabs(a[i][i]) < EPS) {
			cout<<"不存在逆矩阵"<<endl;
			return ;
		}
		//这里就是将第i行下面所有行的第i列清空，变成一个阶梯型的矩阵
		double aii_inv = 1.0/a[i][i];
		//将第i行都乘上a[i][i]的逆
		a[i][i] = 1.0;
		for(ll j = i + 1;j <= n ; ++j) {
			a[i][j] = a[i][j] * aii_inv;
		}
		for(ll j = 1;j <= n; ++j) {
			b[i][j] = b[i][j] * aii_inv;
		}
		//将第i行下面的所有第i列的元素值清空
		for(ll j = i + 1;j <= n; ++j) {
			for(ll k = i + 1;k <= n; ++k) {
				a[j][k] = a[j][k] - a[i][k] * a[j][i];
			}
			for(ll k = 1;k <= n; ++k) {
				b[j][k] = b[j][k] - b[i][k] * a[j][i];
			}
			a[j][i] = 0.0;
		}
	}
	output(a,b);
	//从下往上第推删除A矩阵第i列后的所有元素
	for(int i = n; i >= 1; -- i) {
		for(int j = i - 1;j >= 1; --j) {
			for(int k = 1;k <= n; ++k) {
				//处理的是第i行和第j行的数据
				b[j][k] = b[j][k] -  a[j][i] * b[i][k];
			}
			a[j][i] = 0.0;
		}
	}
	cout<<"A矩阵的逆矩阵："<<endl;
	//到了这里说明A矩阵已经变为单位矩阵了，此时的B矩阵就是A矩阵的逆矩阵了
	for(int i = 1;i <= n; ++i) {
		for(int j = 1;j <= n; ++j) {
			cout<<b[i][j]<<"\t\n"[j == n];
		}
	}
	
}

int main()
{
	string s;
	cin>>n;
	for(int i = 1;i <= n; ++i) 
		for(int j = 1;j <= n; ++j) {
			cin>>a[i][j];
			b[i][j] = (i==j?1.0:0.0);
		}
	guss();
	return 0;
}
/*
A
3
2 1 1
3 2 1
2 1 2

逆矩阵：
3 -1 -1
-4 2 1
-1 0 1	
*/

六、拓展：逆矩阵求法

至于这一部分的资料，大家可以自行搜索噢

6.1 LU分解法

LU分解法其实是高斯消元法的一种变种算法。LU分解是将矩阵A分解为一个下三角矩阵与一个上三角矩阵的乘积。所谓的三角阵就是一半为零的矩阵。L是下三角矩阵(Lower TriangularMatrix)，即主对角线以上的元素全部都是0的矩阵。U是上三角矩阵(Upper Triangular Matrix)，即主对角线以下的元素全部都是0的矩阵。

$$\begin{gathered} A=LU \\ {A}^{-1}=U^{-1}{L}^{-1} \end{gathered}$$
然LU分解是高斯消元法的一种表现形式，但是相对于高斯消元法，LU分解更易于实现并行化。计算机基本用这种方法。比如求 $50000\times 50000$ 的这种大型矩阵。

6.2 SVD分解法

SingularValue Decomposition分解法也叫做奇异值分解，也是线性代数中十分重要的矩阵分解法，同样的能用来求解矩阵的逆矩阵。不同于LU分解中将矩阵A分解为下三角矩阵L与上三角矩阵U的乘积，SVD分解将矩阵A分解为三个矩阵的乘积，分别为：正交矩阵U、对角矩阵W以及正交矩阵V的转置矩阵V.

$$\begin{gathered} A=UW{V}^T \\ {A}^{-1}=V{W}^{-1}{U}^T \end{gathered}$$

6.3 QR分解法

QR分解同样将原始矩阵A分解为两个矩阵的乘积，不同的是这两个矩阵分别为正交矩阵Q和上三角矩阵R。

$$\begin{gathered} A=QR \\ {A}^{-1}=R^{-1}{Q}^{-1} \end{gathered}$$