2020安徽省大学生程序设计大赛题解——D 字符串修改
D 字符串修改
对于两个由0与1组成的长度均为N的序列S和T,f (S,T)定义如下:
重复如下操作,使得序列S与序列T相同。f (S,T)是经过操作后,所需要的最少的花费。
改变S[i]的值(O改为1或者1改为0),它的花费为DC[i],其中D是在此操作之前,序列中满足S[j]≠T[j]的j的个数(1K<=j<=N)。C[i]表示对i位置进行变换的代价。
对于一个固定长度N,共有2N (2N-1)对由01组成的序列(S,T),计算所有f(S,T)的总和,并输出它对10+7的结果。
题目

标签
快速读入、快速幂
分析
本题的第一个难点在于理解题意,想要理解题意,首先要知道题目中这句话的描述是什么意思——
对于一个固定长度 N,共有 2 N × ( 2 N − 1 ) 对由 01 组成的序列(S,T) \textit{对于一个固定长度 N,共有$2^N \times (2^N-1)$对由 01 组成的序列(S,T)} 对于一个固定长度 N,共有2N×(2N−1)对由 01 组成的序列(S,T)
以
N
=
2
N=2
N=2为例,则
0
0
0、
1
1
1可以组成
00
00
00、
01
01
01、
10
10
10、
11
11
11四种
01
01
01对,这四种
01
01
01对有
A
4
2
A_4^2
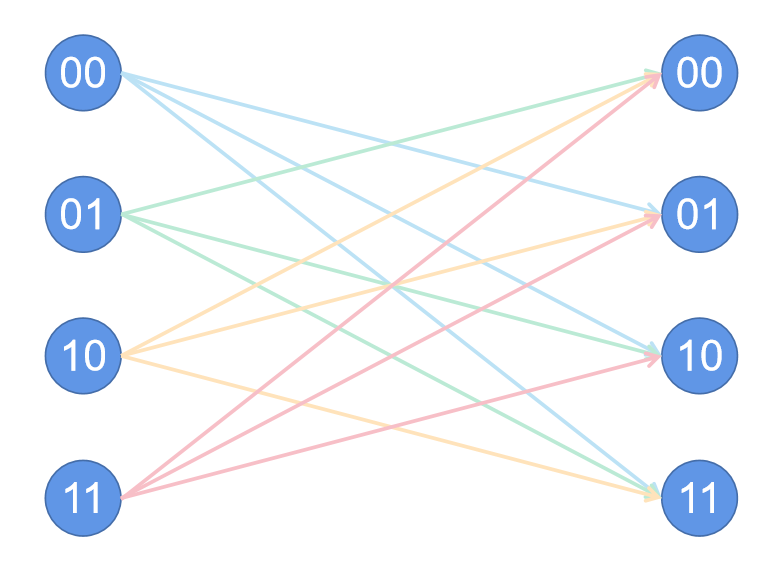
A42种对应方式,如下图所示。
图
D
−
1
对
于
样
例
数
据
二
的
展
示
图D-1 \ \ \ \ 对于样例数据二的展示
图D−1 对于样例数据二的展示
由此可以推导出,长度为 N N N的子串,可以组成 2 N 2^N 2N个 01 01 01对,这些 01 01 01对有 A 2 N 2 A_{2^N}^2 A2N2种对应方式。充分理解这句话,是解决此问题的必要条件。
如果分析这么多种对应方式,那显然是一项庞大的工作,因此我们考虑对这个问题进行简化。
简化的切入点是不同对应方式的异同点上,不难发现,每一个 f ( S , T ) f(S,T) f(S,T),其花费 c o s t cost cost只和 S S S和 T T T两子串对等位置上不同的元素数量有关。例如 1001 1001 1001到 0111 0111 0111,有 [ 0 ] [0] [0] [ 1 ] [1] [1] [ 2 ] [2] [2]三个对等位置的元素不同。我们定义 S S S、 T T T对等位置的不同元素数量为 x x x,则每一对 S S S、 T T T都对应一个 c o s t ( x ) cost(x) cost(x)。

图
D
−
2
对
c
o
s
t
(
x
)
的
展
示
图D-2 \ \ \ \ 对cost(x)的展示
图D−2 对cost(x)的展示
基于此,我们把问题简化为求解所有 f ( S , T ) f(S,T) f(S,T)对应的 c o s t ( x ) cost(x) cost(x)。换言之,本题的求解被拆分为了两个子问题:
子问题一:对于给定的 f ( S , T ) f(S,T) f(S,T),确定最小的 c o s t ( x ) 对 应 的 方 案 cost(x)对应的方案 cost(x)对应的方案
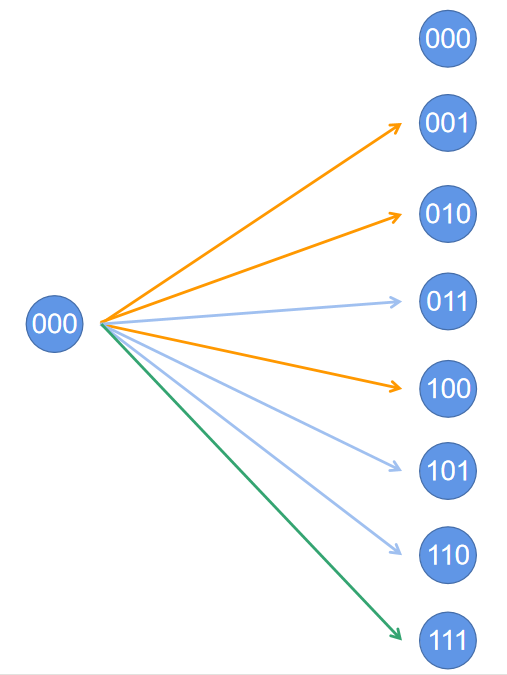
我们以 N = 3 N=3 N=3为例,只需要讨论一种 S S S对应的所有 T T T的情况,即可推出所有的 f ( S , T ) f(S,T) f(S,T),因为这样的映射关系存在对称性。当 N = 3 N=3 N=3时,取 S = 000 S=000 S=000,并用橙色表示 x = 1 x=1 x=1的 f ( S , T ) f(S,T) f(S,T),用蓝色表示 x = 2 x=2 x=2,绿色表示 x = 3 x=3 x=3的情况如下图所示。
图
D
−
3
S
=
000
时
,
f
的
所
有
情
况
图D-3 \ \ \ \ S=000时,f的所有情况
图D−3 S=000时,f的所有情况
想要让总花费最小,则需要让变换次数较小的位置做变换代价较高的变换,然而,每个坐标的变换代价一致,因此想改变每次变换的花费只能从改变坐标变换的次序入手。
我们以 c o s t ( 3 ) cost(3) cost(3)为例,可以得出 c o s t ( 3 ) = c s t [ 1 ] × 1 + c s t [ 2 ] × 2 + c s t [ 3 ] × 3 cost(3)=cst[1] \times 1+cst[2] \times 2+cst[3] \times 3 cost(3)=cst[1]×1+cst[2]×2+cst[3]×3,其中 c s t [ i ] cst[i] cst[i]是在 f ( S , T ) f(S,T) f(S,T)有i个位置元素不同。很自然的想到,对于每个 f ( S , T ) f(S,T) f(S,T),先让变换代价较小的位置进行变换是最优的解决方案。
因此我们对数组 c c c进行由大到小的排序,考虑到整个问题具有轮换对称性,我们不失一般性的只分析 c [ 0 ] < c [ 1 ] < c [ 2 ] c[0]<c[1]<c[2] c[0]<c[1]<c[2]的情况。
图
D
−
4
S
=
000
时
,
最
优
的
变
换
代
价
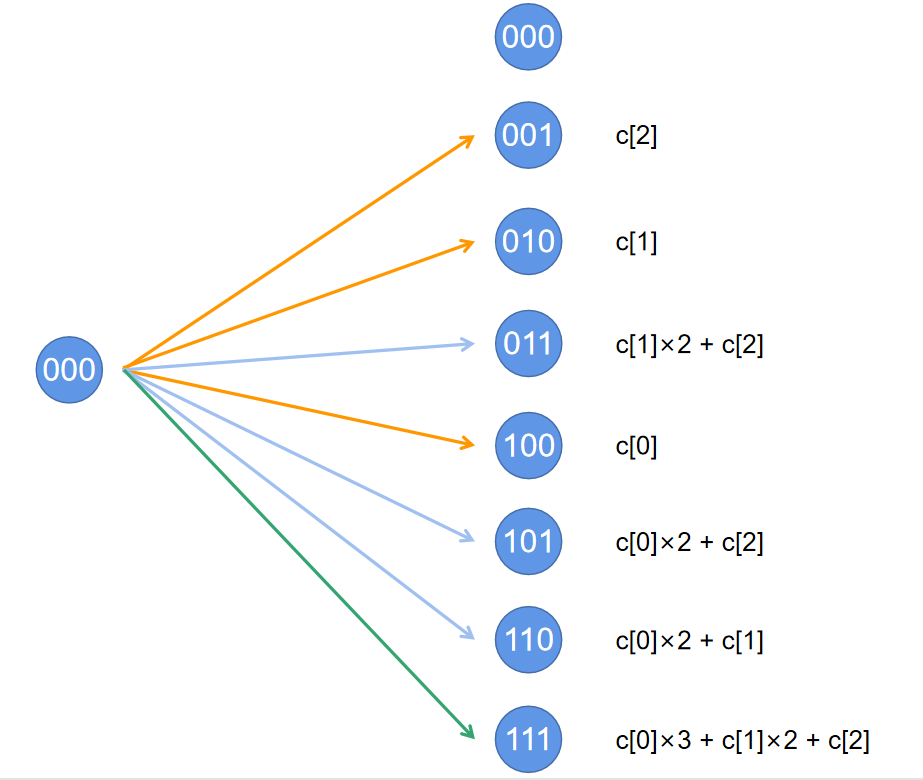
图D-4 \ \ \ \ S=000时,最优的变换代价
图D−4 S=000时,最优的变换代价
上图中,橙色线表示 x = 1 x=1 x=1时每个对应关系的 c o s t cost cost,蓝色、绿色同理。依此,我们得出了每个 f ( S , T ) f(S,T) f(S,T)的最优方案。下面的工作会将其抽象成具体的数学公式。
子问题二:求解 x x x的所有可能取值,记录相应的总花费
x x x的取值范围显然是小于等于 N N N的所有正整数。我们依此分析 x x x的不同取值对应的结果,并探究其规律。
x
=
1
x=1
x=1时,显然
c
o
s
t
(
1
)
=
Σ
c
[
i
]
cost(1)=\Sigma c[i]
cost(1)=Σc[i]
x
=
2
x=2
x=2时,图
D
−
4
D-4
D−4给出了答案——
c
[
0
]
×
4
+
c
[
1
]
×
3
+
c
[
2
]
×
2
c[0] \times 4 +c[1] \times 3 +c[2] \times 2
c[0]×4+c[1]×3+c[2]×2
x
=
3
x=3
x=3时,答案为
c
[
0
]
×
3
+
c
[
1
]
×
2
+
c
[
2
]
c[0] \times 3 + c[1] \times 2 +c[2]
c[0]×3+c[1]×2+c[2]
以上结果相加得 c [ 0 ] × 8 + c [ 1 ] × 6 + c [ 2 ] × 4 c[0] \times 8 + c[1] \times 6 +c[2] \times 4 c[0]×8+c[1]×6+c[2]×4,对应的数学表达式恰好满足 a n s = Σ c [ i ] ∗ ( i + 2 ) ∗ 2 N − 2 ans = \Sigma c[i] * (i + 2) * 2 ^{N-2} ans=Σc[i]∗(i+2)∗2N−2
能够得出这样的表达式,其原因并非一昧的臆测规律。我们以 x = 2 x=2 x=2为例,易证变换代价最大的位置,其每次变换都会在其他位置完成变换之后;相应的,变换代价最小的位置每次变换都在最前。对于确定的 N N N、 x x x,变换代价最大的位置变换 C N − 1 x − 1 C _{N-1} ^{x-1} CN−1x−1次,变换代价最小的位置变换 C N − 1 x − 1 + N − 1 C _{N-1} ^{x-1} + N - 1 CN−1x−1+N−1次。即,所有位置按照变换代价从大到小排序,形成从 C N − 1 x − 1 C _{N-1} ^{x-1} CN−1x−1到 C N − 1 x − 1 + N − 1 C _{N-1} ^{x-1} + N - 1 CN−1x−1+N−1的公差为 1 1 1的等差数列。
基于上述规律,我们便可得出一般性规律,即 a n s = Σ c [ i ] ∗ ( i + 2 ) ∗ m i ans = \Sigma c[i] * (i + 2) * mi ans=Σc[i]∗(i+2)∗mi,其中 m i = 2 N − 2 mi = 2 ^{N-2} mi=2N−2。
这是单一的 S S S对应的花费, S S S共有 2 N 2^N 2N种取值可能,因此最终结果为 a n s ∗ 2 N ans * 2^N ans∗2N
问题到这里还没有结束,我们的数据范围较大,用朴素的幂或者内置的 p o w pow pow函数不能计算如此大的数。因此我们引入快速幂算法计算上述公式中出现的幂次的值。
快速幂算法如下:
快速幂的目的是做到快速求幂,假设我们要求 a b a^b ab,按照朴素算法就是把 a a a连乘 b b b次,这样一来时间复杂度是 O ( b ) O(b) O(b)也即是 O ( n ) O(n) O(n)级别,快速幂能做到 O ( l o g n ) O(logn) O(logn),快了很多。
我们都学习过进制与进制的转换,知道一个 b b b进制数的值可以表示为各个数位的值与权值之积的总和。比如, 2 2 2进制数 1001 1001 1001,它的值可以表示为 10 10 10进制的 1 ∗ 2 3 + 0 ∗ 2 2 + 0 ∗ 2 1 + 1 ∗ 2 0 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0 1∗23+0∗22+0∗21+1∗20,即 9 9 9。这完美地符合了上面的要求。可以通过 2 2 2进制来把 n n n转化成 2 k m 2^{km} 2km的序列之和,而 2 2 2进制中第 i i i位(从右边开始计数,值为 1 1 1或是 0 0 0)则标记了对应的 2 ( i − 1 ) 2^(i - 1) 2(i−1)是否存在于序列之中。譬如, 13 13 13为二进制的 1101 1101 1101,他可以表示为 2 3 + 2 2 + 2 0 2^3 + 2^2 + 2^0 23+22+20,其中由于第二位为 0 0 0, 2 1 2^1 21项被舍去。
如此一来,我们只需要计算 a 、 a 2 、 a 4 、 a 8 . . . . . . a ( 2 k m ) a、a^2、a^4、a^8......a^(2^km) a、a2、a4、a8......a(2km)的值(这个序列中的项不一定都存在)并把它们乘起来即可完成整个幂运算。借助位运算的操作,可以很方便地实现这一算法,其复杂度为 O ( l o g n ) O(logn) O(logn)。
typedef long long ll;
const int M = 1e9 + 7;
ll quick_pow(ll x, ll n, ll m = M) {
ll res = 1;
while (n > 0) {
if (n & 1) res = res * x % m;
x = x * x % m;
n >>= 1;
}
return res;
}
样例所需读入数据也具有不小的规模,我们引入了快速读入算法。
typedef long long ll;
inline ll read() {
register ll x = 0, f = 1; char ch = getchar();
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) { x = (x << 3) + (x << 1) + ch - '0'; ch = getchar(); }
return (f == 1) ? x : -x;
}
参考答案(C++)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M = 1e9 + 7;
inline ll read() {
register ll x = 0, f = 1; char ch = getchar();
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) { x = (x << 3) + (x << 1) + ch - '0'; ch = getchar(); }
return (f == 1) ? x : -x;
}
ll quick_pow(ll x, ll n, ll m = M) {
ll res = 1;
while (n > 0) {
if (n & 1) res = res * x % m;
x = x * x % m;
n >>= 1;
}
return res;
}
bool cmp(int a, int b) {
return a > b;
}
ll ans, n;
int main() {
n = read();
if (n == 1) {
ll temp = read();
cout << temp * 2 % M;
return 0;
}
ll mi = quick_pow(2, n - 2);
ll* c = new ll[n + 1];
for (ll i = 0; i < n; i++) {
c[i] = read();
}
sort(c, c + n, cmp);
for (ll i = 0; i < n; i++) {
ans += c[i] * (i + 2) * mi % M;
ans %= M;
}
cout << ans * quick_pow(2, n) % M;
}






















 1132
1132











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








