动态规划自我总结

动态规划总体思想

动态规划的基本思想：

利用空间换取时间，一种自底向上的求解策略，记录中间过程，来避免大量的重复运算。

动态需要满足三个条件：

1. 最优子结构性质
2. 无后效性
3. 重叠子问题性
   这三条性质针对的方向不同：
   解释1：即问题的最优策略序列的子序列最优。即最优子问题最终可以推出原问题的最优解。
   解释2：子问题之间相互独立，各个子问题解决后不会对后面子问题的解决产生影响。
   解释3：子问题实现的方法与策略应该是一样的，性质不变。

动态规划实现步骤

1. 验证最优子结构性质；
2. 建立递归式；
3. 自底向上求取最优；
4. 根据找到的最优值回溯，找到最优序列。

说明：如果题目仅仅要求求取最优值，则前三布实现后就可以停止了。

动态规划具体实例

Fibonacci数：

利用数组，存储算出的数字，这样就避免了大量的初始值的重复运算

如图所示，
如果利用表，把f（18）记录下来 ， 则绿色框中的运算可以省去，直接查表可得；
同理，如果记录下f（17）的数字，则蓝色框中的计算可以省去，直接查表可得，依此类推。

多段图最短路径：

描述：

递归关系：

0/1背包问题：

递归关系：

f ( i ,y ) 为以背包容量y，放置物品 i，… ，n得到的优化效益值：

f ( 1 , y ) = max ( f ( 2 , c ) , f ( 2 , c - w[1] ) + v[1] );
f ( i , y ) = max ( f ( i+1 , y ) , f ( i+1 , y - w[i] ) + v[i] ) 当y > w[i]时；
f ( i , y ) = f ( i+1 , y ) 当 y < w[i]时；

边界条件：
f ( n , y ) = v[n] ; w[n] <= y;
f ( n , y ) = 0 ; w[n] > y;

学会填表

void dynamic( ){
	for ( int i = 0 ; i < w; i++ )
		dp[0][i] = 0;
	for ( int i = 0 ; i < n; i++ )
		dp[i][0] = 0;
		//填表的边界条件
	for ( int i = 1 ; i <= n ; i++ ){
		for ( int j = 1 ; j <= w ; j++ ) {
		if ( j  < w[i] ) 
			dp[i][j] = dp[i+1][j];
		else{
			dp[i][j] = max ( dp[i+1][j] , dp[i+1][j-w[i]] + v[i] );
			}
		}//注意递归关系的应用	
}

回溯：

void find ( int i , int j ) {
	if ( i >= 0 ) {
		if ( dp[i][j] ==dp[i-1][j] ){
			item[i] = 0;
			find ( i-1 , j );
			}
		else if ( dp[i][j] != dp[i-1][j] && 
				  dp[i][j] == dp [i-1][j-w[i]]+ v[i] &&
				  j-w[i] >= 0 ) {
				  item[i] = 1;
				  find ( i-1 , j-w[i] ) ;
			}//注意回溯时递归关系的逆运用
		}
}

元组法的重要应用：

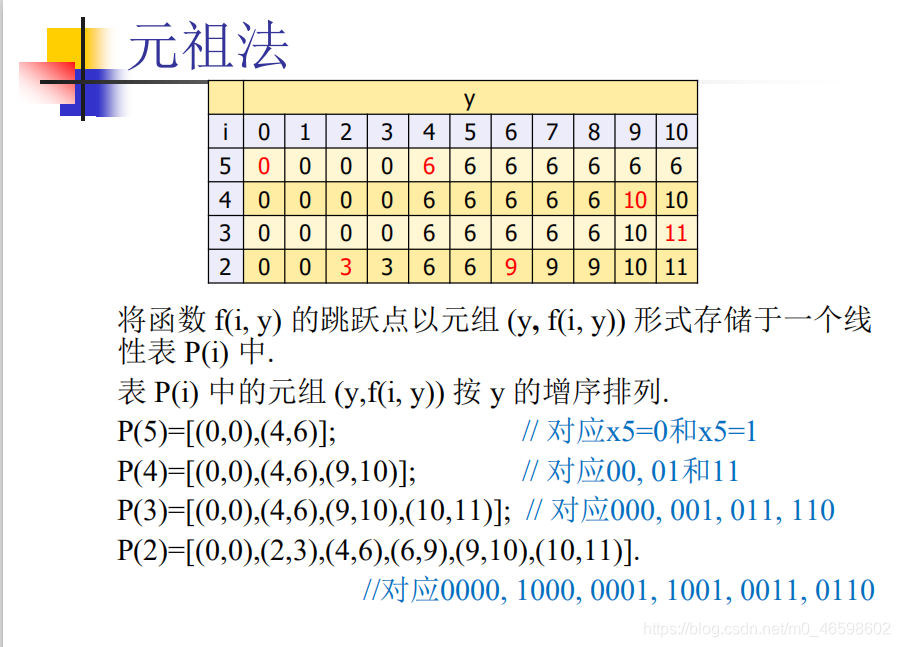
完全背包，多重背包问题：

递归式
c ( i , y ) = c ( i+1 , y ) 当 y < w[i]时；
c ( i , y ) = max ( c ( i+1 , y ) , c( i+1, y-k*w[i] ) + v[i]k ) 当 y >= kw[i]时；
完全背包问题是01背包的一个扩展，求解该问题，可以在01背包第二个条件分支内，加一个循环，判断加入题目要求数量件以后，是否超重，其他的差不太多。

int result = 0; 
if (i ==  0 || c  == 0){ // 初始条件
 	result = 0; 
 	} 
 else if(w[i] > c)
 { // 装不下该珠宝
 result = ks2(i-1, c); 
} 
 else { // 可以装下，取k个物品，取其中使得价值最大的
 	for (int k = 0; k ≤ mi && k ⋅ wi ≤ c; k++){ 
 		int tmp2 = ks2(i-1, c - w[i] ⋅ k) + v[i] ⋅ k; 
 		if (tmp2 > result){ 
 			result = tmp2; 
 		} 
 	} 
 } 
 results[i][c] = result; 
 return result;

矩阵乘法链：

递归条件：

c ( i , j ) = 0 ( if i = j )
c ( i , j ) = ri * ri+1 * ri+2 ( if j = i+1 )
c ( i , j ) = min ( c ( i , k ) + c ( k+1 , j ) + ri*r(k+1) *r(j+1) ) ( if j > i+1 )

伪代码：

void MatrixChain(int r[], int q, int **c, int **kay)
{
	for (int i=1; i<q; i++){
	c[i][i] = 0; // 边界 i = j 的情况
	c[i][i+1] = r[i]*r[i+1]*r[i+2];// 次边界 j = i+1 的情况
	kay[i][i+1] = i;
}
c[q][q] = 0;
for (int s = 2; s< q; s++){
	for (int i = 1; i <= q – s; i++){
	//k = i 时的最小项
	c[i][i+s]=c[i][i]+c[i+1][i+s]+r[i]*r[i+1]*r[i+s+1];
	kay[i][i+s] = i;
	for (int k=i+1; k<i+s; k++){
		int t=c[i][k] + c[k+1][i+s]+r[i]*r[k+1]*r[i+s+1];
		if (t < c[i][i+s]){
			//更小的最小项	
			c[i][i+s] = t;
			kay[i][i+s] = k; 
		}
	 } 
	}
  }
 }

ALL-PAIR 最短路径问题：

递归关系
Cij（k） = min ( Cij( k-1 ) , Cik（k-1）+ Ckj（k-1））；
具体实现主要是维护一个矩阵：

查找序列，主要是维护一个前驱矩阵：

TSP问题：

不多说，直接上图，虽然我觉得TSP用动态规划有点牵强。

总结：

动态规划十分重要，注意记录中间过程的思想，以及学会填表，记住递归式，就可以轻松解决很多问题。