一、算法要求
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。
他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或总旅费)最小。
1. 思路
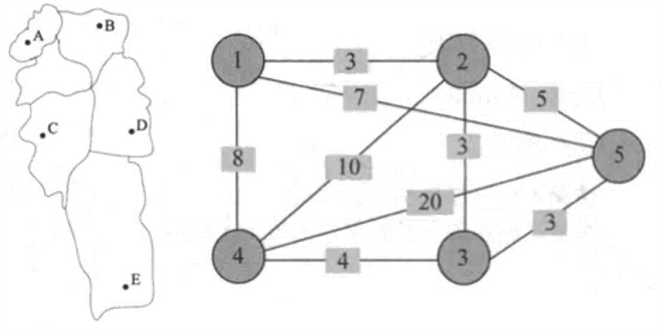
现在我们从景点A出发,要去B、C、D、E共4个景点,按上面顺序给景点编号1~5,每个景点用一个结点表示,可以直接到达的景点有连线,连线上的数字代表两个景点之间的路程(时间)。那么要去的景点地图就转化成了一个无向带权图。
在无向带权图G=(V,E)中,结点代表景点,连线上的数字代表景点之间的路径长度。我们从1号结点出发,先走哪些景点,后走哪些景点呢?只要是可以直接到达的,即有边相连的,都是可以走的。问题就是要找出从出发地开始的一个景点排列,按照这个顺序旅行,不重复地走遍所有景点回到出发地,所经过的路径长度是最短的。
因此,问题的解空间是一棵排列树。显然,对于任意给定的一个无向带权图,存在某两个景点之间没有直接路径的情况。也就是说,并不是任何一个景点排列都是一条可行路径(问题的可行解),因此需要设置约束条件,判断排列中相邻的两个景点之间是否有边相连,有边的则可以走通;反之,不是可行路径。另外,在所有的可行路径中,要求找出一条最短路径,因此需要设置限界条件。
二、完整代码
1. 主文件
main.cpp:
// Project4: 着色问题
#include"Improve1.h"
#include <iostream>
#include <iomanip>
using namespace std;
const int N = 4;//图的顶点数
template<class Type>
class Traveling{
friend int main();
public:
Type BBTSP(int v[]);
private:
int n; //图G的顶点数
Type** a, //图G的邻接矩阵
NoEdge, //图G的无边标识
cc, //当前费用
bestc; //当前最小费用
};
//用最小堆表示活结点优先队列
template<class Type>
class MinHeapNode {
friend Traveling<Type>;
public:
operator Type() const {
return lcost;
}
private:
Type lcost, //子树费用的下届
cc, //当前费用
rcost; //x[s:n-1]中顶点最小出边费用和
int s, //根节点到当前节点的路径为x[0:s]
* x; //需要进一步搜索的顶点是x[s+1,n-1]
};
//优先队列式分支限界法
template<class Type>
Type Traveling<Type>::BBTSP(int v[]){
MinHeap<MinHeapNode<Type>> chessBoard(1000); //定义最小堆的容量为1000
Type* MinOut = new Type[n + 1];
//计算MinOut[i] = 顶点i的最小出边费用
Type MinSum = 0; //最小出边费用和
for (int i = 1; i <= n; i++){
Type Min = NoEdge;
for (int j = 1; j <= n; j++){
if (a[i][j] != NoEdge && (a[i][j] < Min || Min == NoEdge)){
Min = a[i][j];
}
}
if (Min == NoEdge){
return NoEdge; //无回路
}
MinOut[i] = Min;
MinSum += Min;
}
//初始化
MinHeapNode<Type> E;
E.x = new int[n];
for (int i = 0; i < n; i++){
E.x[i] = i + 1;
}
E.s = 0; //根节点到当前节点路径为x[0:s]
E.cc = 0; //当前费用
E.rcost = MinSum; //最小出边费用和
Type bestc = NoEdge;
//搜索排列空间树
while (E.s < n - 1) { //非叶结点
if (E.s == n - 2){ //当前扩展节点是叶节点的父节点
//再加2条边构成回路,所构成回路是否优于当前最优解
if (a[E.x[n - 2]][E.x[n - 1]] != NoEdge && a[E.x[n - 1]][1] != NoEdge &&
(E.cc + a[E.x[n - 2]][E.x[n - 1]] + a[E.x[n - 1]][1] < bestc ||
bestc == NoEdge)) {
//费用更小的回路
bestc = E.cc + a[E.x[n - 2]][E.x[n - 1]] + a[E.x[n - 1]][1];
E.cc = bestc;
E.lcost = bestc;
E.s++;
chessBoard.Insert(E);
}
else{
delete[] E.x; //舍弃扩展节点
}
}
else{ //产生当前扩展节点的儿子节点
for (int i = E.s + 1; i < n; i++) {
if (a[E.x[E.s]][E.x[i]] != NoEdge) {
Type cc = E.cc + a[E.x[E.s]][E.x[i]]; //可行儿子节点
Type rcost = E.rcost - MinOut[E.x[E.s]];
Type b = cc + rcost; //下界
if (b < bestc || bestc == NoEdge) { //子树可能含有最优解
//节点插入最小堆
MinHeapNode<Type> N;
N.x = new int[n];
for (int j = 0; j < n; j++){
N.x[j] = E.x[j];
}
N.x[E.s + 1] = E.x[i];
N.x[i] = E.x[E.s + 1];
N.cc = cc;
N.s = E.s + 1;
N.lcost = b;
N.rcost = rcost;
chessBoard.Insert(N);
}
}
}
delete[]E.x; //完成节点扩展
}
if (chessBoard.Size() == 0) {
break; //堆空
}
chessBoard.DeleteMin(E); //取下一扩展节点
}
if (bestc == NoEdge) {
return NoEdge;//无回路
}
//将最优解复制到v[1:n]
for (int i = 0; i < n; i++) {
v[i + 1] = E.x[i];
}
while (true) {//释放最小堆中所有节点
delete[]E.x;
if (chessBoard.Size() == 0) {
break; //堆空
}
chessBoard.DeleteMin(E); //取下一扩展节点
}
return bestc;
}
int main()
{
int bestx[N + 1],
** a = new int* [N + 1], //用a[][]存储邻接矩阵
simpleArray[4][4] = { {0,30,6,4},
{30,0,5,10} ,
{6,5,0,20} ,
{4,10,20,0} };
cout << "\nThe number of vertices in the graph: n = " << N << endl;
//初始化对应位置的邻接矩阵
for (int i = 0; i <= N; i++) {
a[i] = new int[N + 1];
}
//输出数据输入情况
cout << "\nThe adjacency matrix of the graph is as follows: " << endl;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
a[i + 1][j + 1] = simpleArray[i][j];
cout << "|" << setw(4) << a[i + 1][j + 1];
}
cout << "|" << endl;
}
Traveling<int> example;
example.a = a;
example.n = N;
cout << "\n#The length of the shortest loop is:" << example.BBTSP(bestx) << endl;
cout << "\n#The path of the shortest loop is:";
for (int i = 1; i <= N; i++) {
cout << setw(3) << bestx[i] << " ==>";
}
cout << setw(3) << bestx[1] << endl;
//析构,**a删除申请的空间
for (int i = 0; i < N + 1; i++) {
delete[]a[i];
}
delete[]a;
return 0;
}
2. 头文件
Improve1.h:
#pragma once
#ifndef __IMPROVE1__
#define __IMPROVE1__
#include <iostream>
using namespace std;
//============================最小堆============================//
template<class T>
class MinHeap{ //最小堆
public:
MinHeap(int maxheapsize = 10) {
maxsize = maxheapsize;
heap = new T[maxsize + 1];
currentsize = 0;
}
~MinHeap() {
delete[]heap;
}
int Size() const {
return currentsize;
}
T Max() {
if (currentsize)
return heap[1];
}
MinHeap<T>& Insert(const T& x);
MinHeap<T>& DeleteMin(T& x);
void Initialize(T x[], int size, int ArraySize);
void Deactivate();
void Output(T a[], int n);
private:
int currentsize, maxsize;
T* heap;
};
template <class T>
void MinHeap<T>::Output(T a[], int n) {
for (int i = 1; i <= n; i++)
cout << a[i] << " ";
cout << endl;
}
template<class T>
MinHeap<T>& MinHeap<T>::Insert(const T& x) {//插入
if (currentsize == maxsize) {
return *this;
}
int i = ++currentsize;
while (i != 1 && x < heap[i / 2]) {
heap[i] = heap[i / 2];
i /= 2;
}
heap[i] = x;
return *this;
}
template<class T>
MinHeap<T>& MinHeap<T>::DeleteMin(T& x)
{
if (currentsize == 0)
{
cout << "Empty heap!" << endl;
return *this;
}
x = heap[1];
T y = heap[currentsize--];
int i = 1, ci = 2;
while (ci <= currentsize)
{
if (ci < currentsize && heap[ci] > heap[ci + 1])
{
ci++;
}
if (y <= heap[ci])
{
break;
}
heap[i] = heap[ci];
i = ci;
ci *= 2;
}
heap[i] = y;
return *this;
}
template<class T>
void MinHeap<T>::Initialize(T x[], int size, int ArraySize) {//初始化
delete[]heap;
heap = x;
currentsize = size;
maxsize = ArraySize;
for (int i = currentsize / 2; i >= 1; i--) {
T y = heap[i];
int c = 2 * i;
while (c <= currentsize) {
if (c < currentsize && heap[c] > heap[c + 1])
c++;
if (y <= heap[c])
break;
heap[c / 2] = heap[c];
c *= 2;
}
heap[c / 2] = y;
}
}
template<class T>
void MinHeap<T>::Deactivate() {
heap = 0;
}
#endif
3. 效果展示
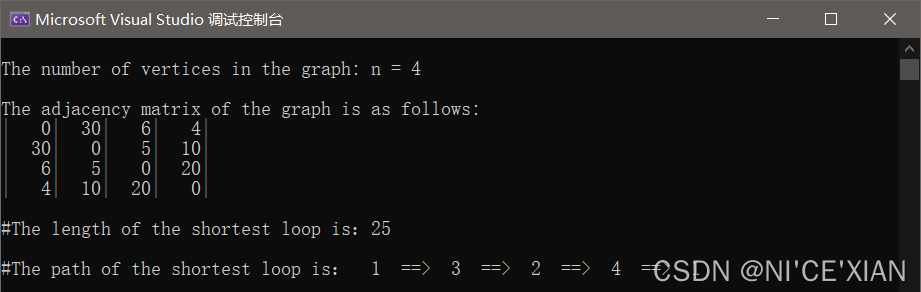
三、补充
(1)时间复杂度
最坏情况下,如图6-46所示。除了最后一层外,有1+n+n(n-1)+…+(n-1)(n-2)…2≤n(n-1)!个结点需要判断约束函数和限界函数,判断两个函数需要O(1)的时间,因此耗时O(n!),时间复杂度为O(n!)。
(2)空间复杂度
程序中我们设置了每个结点都要记录当前的解向量x[]数组,占用空间为O(n),结点的个数最坏为O(n!),所以该算法的空间复杂度为O(n*n!)。
文档供本人学习笔记使用,仅供参考。
























 6957
6957











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










