在低速大功率和高速领域,受限于开关损耗、 散热能力以及系统效率,驱动器开关频率与电机基频的比值(即载波比)往往较低。(有的文献里也叫做基频比)
当载波比低于 15 时,认为电机工作在低载波比工况。
高速场合的载波比低就比较好理解,因为驱动器一般还是10kHz左右,但是电机的转速可能会达到几万转。所以驱动器开关频率与电机基频的比值就很低了。
而大功率场合,电机的电流非常大,这会导致开关器件需要的关断时间相对于低功率场合的开关器件需要的关断时间大幅增加,所以不得不降低开关频率。(有的大功率场合,开关频率只有几百Hz)
我们来看看载波比降低对电机的影响。
仿真参数:
Tpwm = 2e-4;%开关周期
Tspeed = Tpwm;%转速采样周期
Pn = 12;%电机极对数
Ls = 7.5e-3;%定子电感,采用隐极的,Ld=Lq=Ls
Rs = 1;%定子电阻
flux = 0.05627;%永磁体磁链
J = 0.0125;%转动惯量
Vdc = 500;%直流母线电压
iqmax = 20;%额定电流
fc = 300;%电流环带宽
我开关频率5kHz,电机参考转速设为1200r/min以及200r/min。
在1200r/min时,电机的基波频率为1200/60*12Hz,载波比为5000/(1200/60*12)=20.8。这也算得上是一个比较低的载波比了。在200r/min时,电机的基波频率为200/60*12Hz,载波比为5000/(200/60*12)=104。
1.低载波对PI调节器控制效果的影响
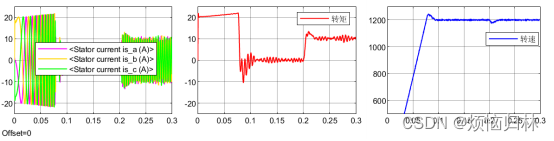
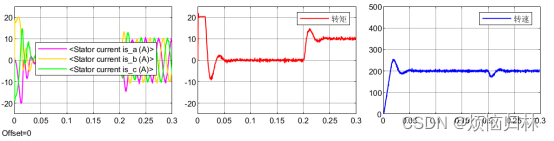
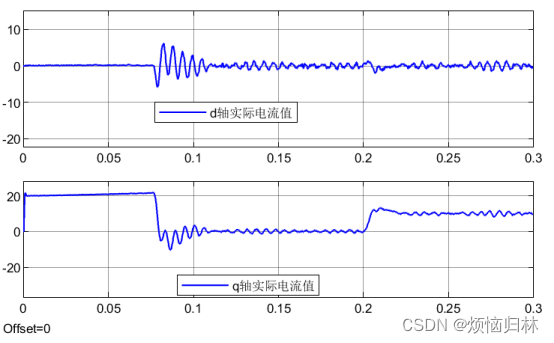
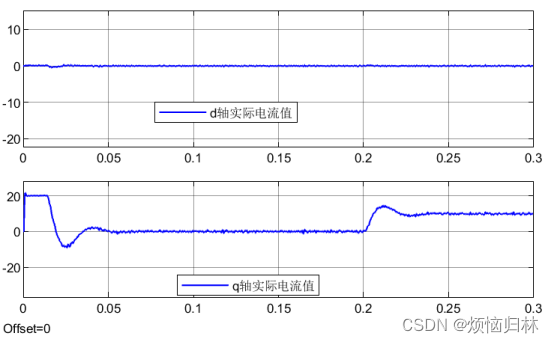
可以看到,由于载波比降低,1200r/min下的d-q电流波形出现了非常明显的脉动。而且我的最大电流设置为20A,在1200r/min时,q轴电流最大值明显超过了20A。
为什么会出现这样的影响呢?
主要就是转子定向不准确造成的。在低载波工况下,如果不考虑转速位置的运动,就会造成很大的电流误差,如下面这幅图所示。而且由于转子定向不准,使得控制器中的dq耦合效应加重,严重影响控制性能。

我们在1200r/min的时候,虽然d-q电流出现波动,但是它们还能在给定值上下波动。比如说d轴电流,d轴电流给定值为0,虽然转子运动会造成定向不准确,但是d轴电流总是在0上下波动的,并没有偏离很远呢。那这是为什么呢????
这是因为PI调节器本身就具有较强的鲁棒性,只要转子位置偏差不要太大,就仍能实现电流的有效控制。这一点我在下面这篇文章已经展示过了。
在这篇知乎中,我还提到了用1.5拍延时补偿来抵消一定的控制延时(如下图所示)。

那我们来看看,在1200r/min的时候,加上1.5拍延时补偿看看有没有效果。


可以看到,加上1.5拍延时补偿之后,相对于原来的情况而言,d-q电流的波动明显消失了,而且q轴电流的超调也没有了。其实对要求不太高的场合,PI调节器+1.5拍延时补偿就足够了。
2.低载波对无差拍预测控制效果的影响
参考文献如下(24年1月刚出的文献):

无差拍预测电流控制(DPCC)的好处,之前也说过好多了。主要就是动态响应速度快且电流内环无需参数整定。
但是,有失必有得,无差拍控制就是预测控制的一种,就是一种开环控制!就是一种开环控制!就是一种开环控制!(重要的事情说三遍!)
为啥?不应该是闭环控制吗?
预测控制的输入就是参考电流以及当前的采样电流,计算出所需的电压之后,经过调制之后作用于电机上。假如当前作用的电流没有达到期望的电流,那么它们之间的差值error,差值error没有其实被反馈到控制器中,这个error之间被忽略了。这就是为什么那么多人要做鲁棒性预测控制的原因!
同样的,我们来看看无差拍在1200r/min以及200r/min下的性能表现:
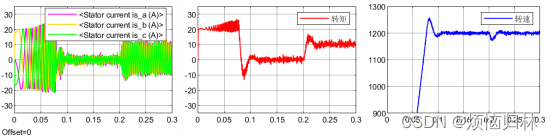
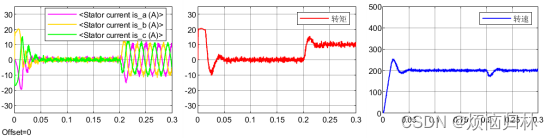
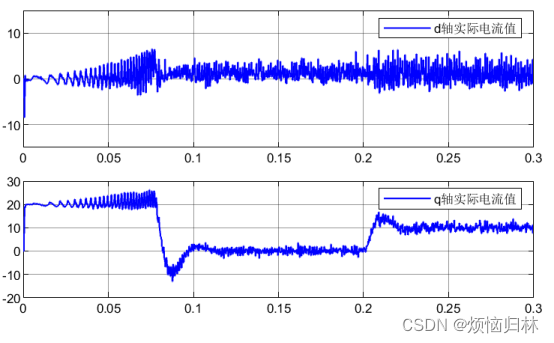
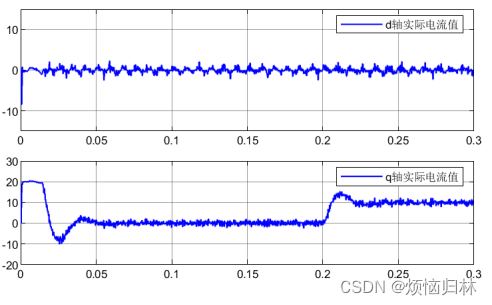
可以看到,即使是在200r/min的情况下,无差拍的性能也是非常差的,远远不如PI。正是因为DPCC是开环控制,没有PI那么强的鲁棒性。而且在1200r/min下,d轴电流明显偏离于0了,q轴电流也有比较明显的超调。
那我们尝试加入1.5拍延时补偿之后看看效果:


加了1.5拍延时之后,DPCC在1200r/min的d轴电流是在0上下波动了(不进行1.5拍延时补偿之前,d轴电流是总在0以上的),q轴电流的超调量也减少了,但是还是具有非常大纹波。
3.采用文献中的低载波比无差拍控制方式

在考虑转子的运动之后,d-q轴上都会出现永磁体磁链的分量。(这个是公式是基于d-q坐标系不动,而转子是运动的前提)
下面这里运用到伏秒平衡原理。(因为电机本身就是一个阻感性负载,运用伏秒平衡原理来简化这些方程,是非常常见的事情。)




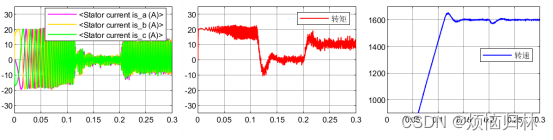
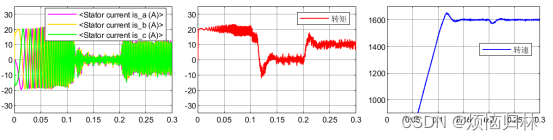
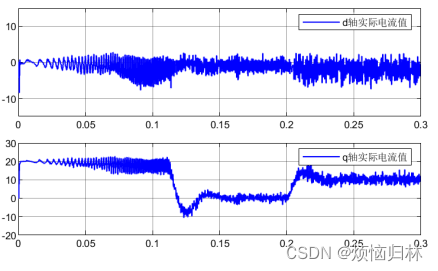
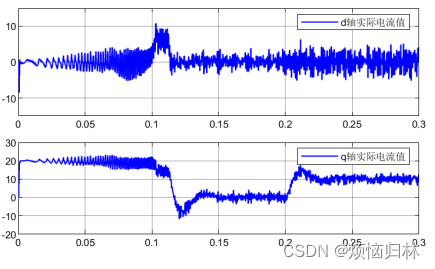
这里可以看到,其实文献中提出的补偿方法,貌似没有多大效果。。。。。。。。。。
然后我分析了原因,看看了论文中电机的参数,发现论文中用的磁链数值比较大!论文中的磁链数值达到了0.18Wb。而我这台仿真电机的磁链仅仅为,flux = 0.05627。而且再回看本文中提出的公式,其贡献主要是考虑了转子运动造成的d轴位置变化,计算了低载波比工况下反电动势的伏秒平衡模型。所以对我这台磁链很小的电机,反电动势位置变化影响其实不大,所以效果也就一般了。
接下来把永磁体磁链扩大了三倍,同时也得把母线电压调一下,不如可能会出现过调制。
flux = 0.05627*3;%永磁体磁链
Vdc = 800;%直流母线电压
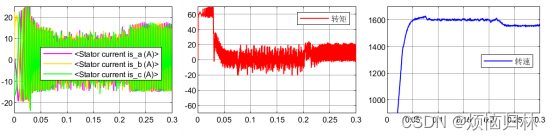
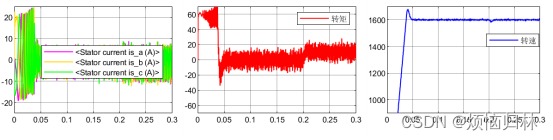
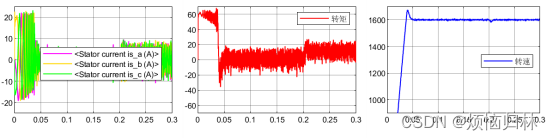
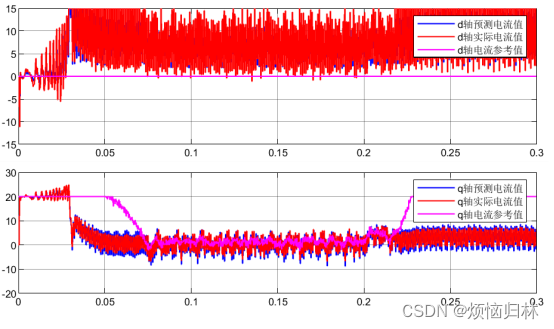
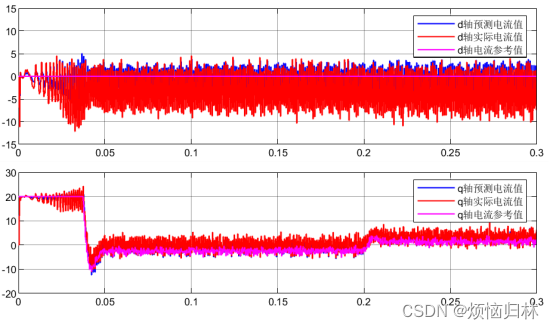
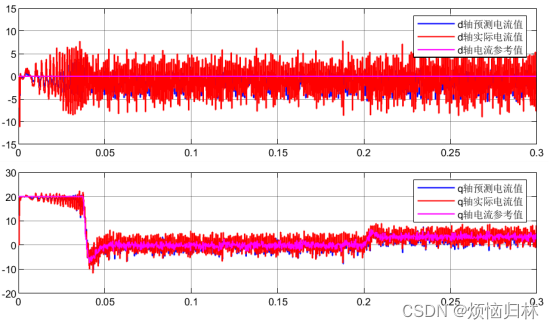
可以看到,将反电势磁链增大之后,提出的方法与传统的无差拍有了一个很明显的效果提升。无补偿的算法根本没有办法稳定于参考转速1600r/min,而且也跟不上参考电流。
但是呢,这篇论文的方法似乎都不如1.5拍延时补偿。。。







 文章探讨了低载波比条件下,驱动器开关频率与电机基频的关系,重点对比了PI调节器与无差拍预测控制(DPCC)在电机控制中的效果。PI调节器展现出更好的鲁棒性,而无差拍控制在低速下性能较差。文中还介绍了1.5拍延时补偿的应用,改善了控制性能。
文章探讨了低载波比条件下,驱动器开关频率与电机基频的关系,重点对比了PI调节器与无差拍预测控制(DPCC)在电机控制中的效果。PI调节器展现出更好的鲁棒性,而无差拍控制在低速下性能较差。文中还介绍了1.5拍延时补偿的应用,改善了控制性能。
 https://zhuanlan.zhihu.com/p/662723204
https://zhuanlan.zhihu.com/p/662723204
















 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










