提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
前言
利用Logistic回归方法对公司审计是否存在风险进行分类,Logistic回归方法进行分类并不需要做很多工作,所需做的只是把测试集上每个特征向量乘以最优化方法得来的回归系数,再将该乘积结果求和,最后输入到Sigmoid函数中即可。
提示:以下是本篇文章正文内容,下面案例可供参考
一、概念解析
1.1机器学习方法
机器学习有三大方法,分类如下:
(1)监督学习:有标准答案的试错学习
(2)无监督学习:根据一定假设寻找数据的内部结构
(3)强化学习:延迟满足,根据结构调整行为
监督学习更为清晰明了的解释如下:给定算法的数据集,其中包含了正确答案。比如给定一个房价的数据集,其中每个样本都给出正确的价格,算法的目的就是给出更多未知的正确房价信息。
监督学习又分为两类:分类问题和回归问题。本质都是对输入做出预测。分类和回归的区别不在于输入,而是输出的值是连续的还是离散的。
1.2 回归
回归分析就是用来探寻变量之间的关系的过程。比如我们想知道房屋价格和房屋面积之间的关系,这里假设二者是线性关系,房屋面积是自变量X,房屋价格是因变量Y,那么二者之间的关系可以简单描述为:Y=F(X)=AX+B+C,C是误差项
在求解系数A、B和参数C的过程就是回归。还是房价问题,我现在假设这个方程的正解A=1,B=1,C=0.我开始的数据集样本空间只有100个,经过训练你得出A=1.5,B=0.8,C=-0.4.随后我扩大了数据集样本空间有10000个样本。经过训练得出结果A=1.001,B=0.992,C=-0.004.这个时候已经非常接近我给出的正解。假如我在给出更大的样本数,它的最终结果会无限接近正解,训练结果不断向正解靠拢的过程就是回归。一开始是错误的,最后样本变多慢慢接近正解,回到正解附近就是回归。通过不断训练得到A,B,C,然后输入一个X,带入关系得到一个预测值Y,这个就是回归。它的输出值是连续的,定量的,也就是说在某个范围内即可,如果所得预测值和真实值的误差最小,则认为这是一个好的回归。回归的目的是为了找到最优拟合,通过回归算法得到一个最优拟合线,这个线可以最好的接近数据集中各个点。
1.3 分类
分类是根据输入特征预测得到一个预测类别,比如房价问题,假设我们已经得出一个训练好的模型,只要给出任意房屋面积之后它都能给出相对正确的房屋价格。现在你要买一套200平的房子,通过模型计算结果需要500w,这个价格你说“贵”,然后又降低标准买120平的,模型一算需要260w,感觉这个比较“便宜”。例子中你听到房屋价格500w和260w的时候你说的“贵”和“便宜”就是分类。它的输出值是离散的、定性的,对就是对,错就是错,什么类别就是什么类别,最终结果只有一个。分类的目的是为了寻找决策边界,即分类算法得到的是一个决策面,用于对数据集中的数据进行分类。
1.4 Logistic回归是回归还是分类
上述例子中模型预测的输出是500和260两个个数字,把我们内心的衡量标准——便宜贵贱转化成具体的量(数字)输出这就是就是定量输出,即为回归;如果我们的输出经过sigmoid函数进行分类,把sigmoid的阈值设置为0.5,输出结果定义为“1(贵)”和“0(不贵)”这样一个类别,就是一个分类问题。这也就是Logistic回归为什么叫回归却是分类问题就是因为sigmoid函数,sigmoid 可以将数据压缩到[0, 1]之间,它经过一个重要的点(0, 0.5)。这样,将输出压缩到[0,1]之间,0.5作为阈值,大于0.5作为一类(贵),小于0.5作为另一类(不贵)。所以Logistic回归是利用sigmoid 函数进行分类的一种模型。
二、Logistic回归分类
1.Sigmoid函数
sigmoid函数是一种阶跃函数,具体计算公式如下:

以下给出Sigmoid函数在不同坐标尺度下的两条曲线图,绘制代码如下:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(inx):
"""
这是sigmoid函数
"""
return 1.0 / (1 + np.exp(-inx))
x_value = np.linspace(-6, 6, 20)
y_value = sigmoid(x_value)
xx_value = np.linspace(-60, 60, 120)
yy_value = sigmoid(xx_value)
# numpy模块中的linspace()函数与arange()函数非常相似。它的前两个参数同样是用来指定序列的起始和结尾,
# 但是第三个参数不再表示相邻两个数字之间的距离,而是用来指定我们想把由开头和结尾两个数字所指定的范围分成几个部分。
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(x_value, y_value)
ax1.set_xlabel('x')
ax1.set_ylabel('sigmoid(x)')
ax2 = fig.add_subplot(212)
ax2.plot(xx_value, yy_value)
ax2.set_xlabel('x')
ax2.set_ylabel('sigmoid(x)')
plt.show()
其中上图的横坐标为-6到6,这时的曲线变化较为平滑;下图横坐标的尺度足够大,可以看到,在x=0点处Sigmoid函数看起来很像单位阶跃函数。而这种类似于阶跃函数的效果正是我们想要的,考虑二分类任务,其输出标记为0和1,而Sigmoid函数将输入值x转化为一个接近0或1的y值,并且其输出值在x = 0附近变化很陡。
为了实现Logistic回归分类器,我们可以在每个特征上都乘以一个回归系数,然后把所有的结果值相加,将这个总和代入Sigmoid函数中,进而得到一个范围在(0,1)之间的数值。任何大于0.5的数据被分为1类,小于0.5的被归入0类。接着就是最佳回归系数的确定。
2.线性回归模型
线性回归的一般形式:
![]()
其中X=(X1,X2,...,Xd)是由d维属性描述的样本,其中Xi是X在第i个属性上的取值。
向量形式可记为:![]()
其中W=(W1,W2,...,Wd)为待求解系数。
线性回归的目的:学习一个线性模型以尽可能准确的预测实值输出标记:
![]() 使得
使得![]()
给定数据集:![]() ,其中
,其中![]()
Xi1表示Xi在第一个属性上的取值。
线性模型试图学得一个通过属性的线性组合来进行预测的函数:
![]()
一般向量形式写为:![]()
其中: ![]()
为了便于讨论,把w,b吸收入向量形式:![]()
变成:![]() ,重新得到f(xi)
,重新得到f(xi)
![]()
3.损失函数
如何确定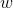 和
和 呢?显然关键在于如何衡量
呢?显然关键在于如何衡量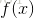 和
和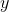 之间的差别。均方误差(亦称为平方损失)是回归任务中最常用的性能度量,因为它求导方便,做梯度优化的时候计算便捷。线性回归依据最小二乘法使得观察值和估计值差的平方和最小。误差形式如下:
之间的差别。均方误差(亦称为平方损失)是回归任务中最常用的性能度量,因为它求导方便,做梯度优化的时候计算便捷。线性回归依据最小二乘法使得观察值和估计值差的平方和最小。误差形式如下:

定义损失函数:

显然此公式是二次方程,有最小值,当它取最小值得时候,所对应的 就是最佳拟合参数。
就是最佳拟合参数。
但这里对于logistic回归而言,我们却不能最小化观察值和估计值的差的平方和,因为这样就会发现J(θ)为非凸函数,就存在多个局部极值点,从而不能开展梯度迭代得到最优参数,所以,这里我们重新定义一种损失函数。








 本文详细介绍了如何运用Logistic回归进行审计风险分类。首先解释了机器学习、回归、分类和Logistic回归的概念,然后深入探讨了Sigmoid函数、线性回归模型、损失函数和梯度上升法。在实践中,通过三种不同的梯度上升方法测试,包括全批量、随机和改进的随机梯度上升,最后展示了Logistic回归在审计风险分类问题上的应用和代码实现。
本文详细介绍了如何运用Logistic回归进行审计风险分类。首先解释了机器学习、回归、分类和Logistic回归的概念,然后深入探讨了Sigmoid函数、线性回归模型、损失函数和梯度上升法。在实践中,通过三种不同的梯度上升方法测试,包括全批量、随机和改进的随机梯度上升,最后展示了Logistic回归在审计风险分类问题上的应用和代码实现。

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








