广义旁瓣相消算法学习笔记

自适应波束形成

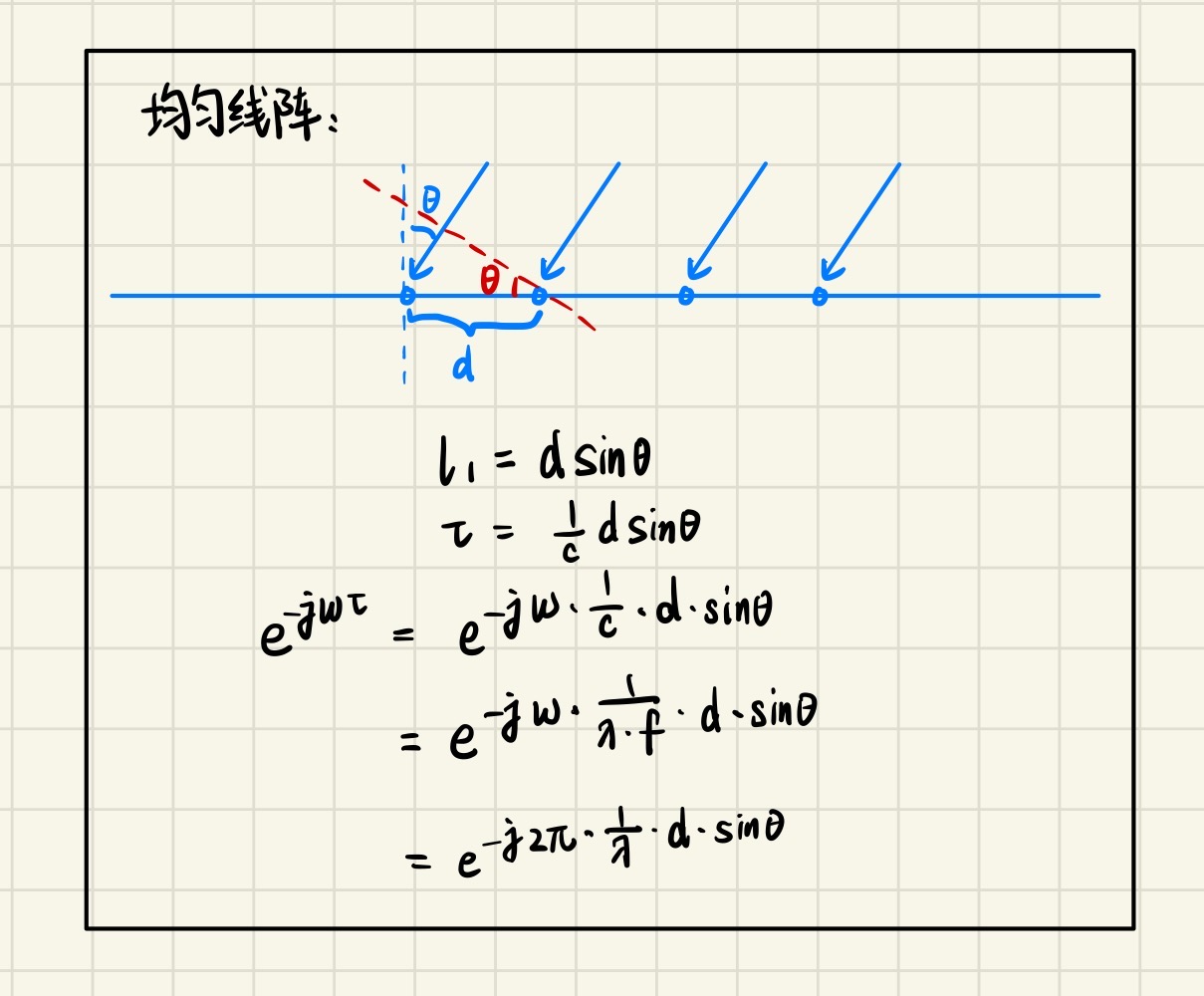
波束形成技术主要用于阵列信号处理中，其主要目的是使阵列天线方向图的主瓣指向所需信号的方向，使其零陷对准于干扰信号方向，尽可能地提高阵列输出所需信号的强度，同时尽可能减小干扰信号的强度和噪声的强度，从而提高阵列输出的信干噪比。

在一个综合系统的设计中，上层的算法需要与下层的硬件结构适配，才能够准确良好地方式运行。波束形成算法也需要考虑对应阵列阵元的空间分布。

为了方便推导，本文使用均匀线阵(ULA)作为空间阵列，在ULA上应用各种波束成形技术。ULA阵列输入信号的表达式由下文可知：

$$X_d(t)=\left[\begin{array}{l}{x}_1(t)\\ x_2(t)\\ \cdots \\ x_N(t)\end{array}\right]=s(t)\left[\begin{array}{l}1\\ e^{j\frac{2\pi }{\lambda }d\sin {\theta }_d}\\ \cdots \\ e^{\frac{2\pi }{\lambda }(N-1)d\sin {\theta }_d}\end{array}\right]=s(t)a({\theta }_d)$$

$$X(t)=s(t)a({\theta }_d)+\sum _{j=1}^{n-1}{s}_j(t)a({\theta }_j)+N(t)$$

根据输入的阵列信号的表达式，波束形成后的输出语音信号$y(t)$为阵列输入$M$个通道经处理后的加权之和。下式中$w$为波束形成器的权值向量。
$$y(t)=\sum _{i=1}^M{w}_i^H(t)x_i(t)=w^{H}X(t)$$

下文中介绍一些常用的波束成形算法，包括其理论和代码仿真。

1. 固定波束成形

固定波束形成技术(Fixed Beamforming)仅仅针对目标方向的信号进行处理，当目标信号入射方向为${\theta }_d$时，阵列对应的导向矢量为$a({\theta }_d)$，若权值向量采用参数$w=a({\theta }_d)$，则对应信号的放大倍数取到最大：
$$y(t)=a^H({\theta }_d)a({\theta }_d)s(t)=Ms(t)$$
此时阵列接受到的各路信号加权相干叠加，是经典的固定波束成形算法。

• 优点：低计算复杂度，易于实现；在非相干噪声场环境下应用较多。
• 缺点：没有充分考虑噪声与干扰；在低信噪比，相干噪声场中效果不佳。

2. 最小方差无失真响应波束形成

1969 年，J. Capon 提出了最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成算法。该算法是应用得最为广泛的自适应波束形成方法之一。

基本原理：调整波束形成器的权值向量，在对目标信号增益不变的情况下，让信号的输出功率降到最低，抑制其他方向的入射信号以及噪声干扰。最终将问题转化为条件极值的优化问题。为简单起见，先不考虑对干扰信号的约束，见下式：
$$\{\begin{array}{l}\underset{x}{\min }{w}^{H}Rw\\ \\ w^{H}a({\theta }_d)=1\end{array}$$
将$w$作为优化问题的目标变量，运用拉格朗日乘数法和矩阵微商的知识，可以求得条件极值问题的最优解：
$$w_{opt}=\mu R^{-1}a({\theta }_d)=\frac{R^{-1}a({\theta }_d)}{a^H({\theta }_d)R^{-1}a({\theta }_d)}$$
因为在输入信号和增益不变的情况下，阵列输出中包含的目标信号的功率不会改变，即$w^H{R}_{d}w$不变，在不考虑入射干扰的条件下，式中的$R_x$可用$R_n$代替，更方便考虑问题。

MVDR算法是理论上广泛使用的波束成形算法，但是因为该算法依赖于阵列信号的协方差矩阵，在实际应用中需要对协方差矩阵进行估计。在复杂情况下，若协方差矩阵计算存在一定偏差，算法性能会大幅度下降。目前衍生出一些基于对角加载的方法，但是复杂度较高。此外，该算法需要提前知道信号的波达方向，在实践中存在一定的困难。

本文针对不考虑干扰信号的MVDR算法，并设置一定的干扰信号测试该算法的抗干扰能力，编写代码code如下：

% Title:    最小方差无畸变响应波束形成器，MVDR
% Author:   Xu Zhe
% Date:     2020-07-25
% Brief:    一维均匀线阵波束形成，MVDR波束形成器

% 系统初始化 Initialization
close all
clear
clc

% 参数 Parameters
M   = 12;               % 阵元数目
c   = 3e8;              % 光速
f   = 10e9;             % 频率
l   = c/f;              % 波长
d   = l/2;              % 阵元间隔 --关注
phi = [10,30]*pi/180;   % 信号和干扰角度
Kt  = 1;                % 目标信号数目
snr = 20;               % 信噪比
inr = 10;               % 干噪比
Ac  = 3601;             % 角度采样数

% 计算阵元位置
R = d * (0:M-1)';

% 计算方向向量
K = length(phi);        % 信号数目
A = zeros(M,K);         % 初始化方向矩阵 Steering Matrix
for k = 1:K
    for m = 1:M
        A(m,k) = exp(1j * 2 * pi * R(m,1)* sin(phi(k))/l);
    end
end

% 构造信号
Ts = 1024;              % 快拍数
Kj = K - Kt;            % 干扰信号数目
% 一个干扰信号，一个目标
s = zeros(K,Ts);        % 信号
sd = zeros(1,Ts);       % 期望信号
for k = 1:Kt
    for i = 0:Ts-1
        s(k,i+1) = sqrt(10^(snr/10)) * exp(1j * 2 * pi * f * i/(2*Ts)); 
    end
    sd = sd + s(k,:);
end
sd = sd/Kt;
if Kj ~= 0
    for k = Kt+1:K
        for i = 0:Ts-1
            s(k,i+1) = sqrt(10^(inr/10)/2) * (randn(1) + 1j*randn(1)) * exp(1j * 2 * pi * f * i/(2*Ts));
        end
    end
end

% 噪声
n = (randn(M,Ts)+1j*randn(M,Ts))/sqrt(2);
% 接收数据向量
x = A * s+n;

% MVDR  --对干扰方向操作了
J = A(:,Kt+1:K) * s(Kt+1:K,:);
Rnj = 1/Ts * (J*J'+n*n');
Rpriv = pinv(Rnj);
w = Rpriv*A(:,1)/(A(:,1)'*Rpriv*A(:,1));

% 方向图
theta = linspace(-pi,pi,Ac);
y = zeros(1,Ac);
for i = 1:Ac
    a = exp(1j * 2 * pi * R(:,1)* sin(theta(i))/l);
    y(i) = w' * a;
end

ydB = 20*log10(abs(y)/max(abs(y)));

% 绘图
figure('name','波束方向图','color',[1,1,1]);
set(gcf,'position',[458,342,290,200])
plot(theta * 180/pi,ydB,'color','b','linestyle','-','linewidth',1);
grid on
xlim([-90,90]);
ylim([-60,0]);
set(gca,'xtick',-90:30:90);
set(gca,'FontName','Times New Roman','FontSize',10.5);
xlabel('Direction of Arrival of the Signal (Degree)','FontSize',10.5);
ylabel('Magnitude Response (dB)','FontSize',10.5);

% 保存
% print('-depsc','E:\07 Latex\Paper Note\figures\MVDR_1.eps');

图1	图2
图3	图4
图5	图6

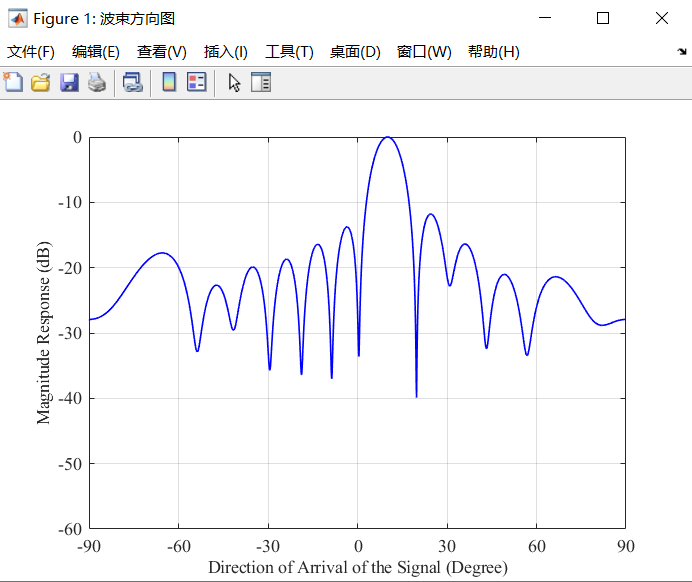
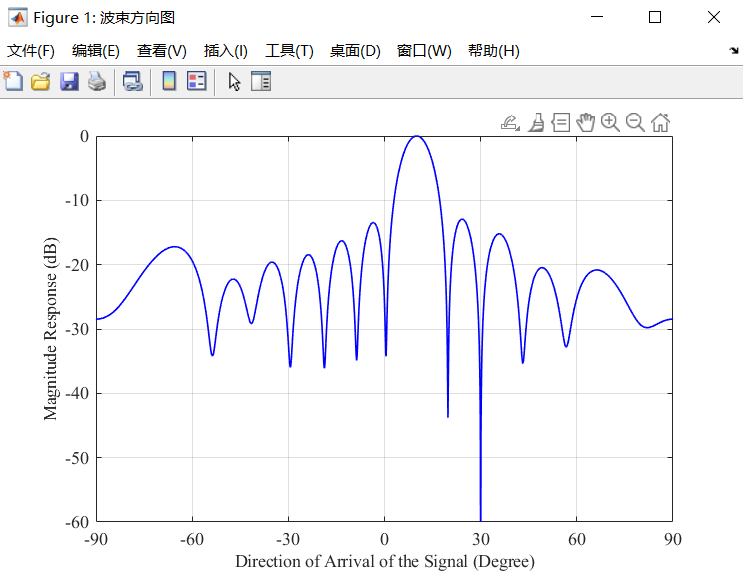
本文使用这组代码在多个实验设置下进行了多组实验，改变了快拍数，干扰信号强度，干扰信号数量以及使用干扰噪声功率$w^H{R}_{nj}w$代替整体信号功率$w^H{R}_{x}w$进行优化的方式，探究这些设置对实验结果的影响，实验结果如上图所示。

默认设置阵元为均匀线阵，包含12个阵元，阵元间距为半波长。信噪比为20dB，干噪比为10dB。设置入射目标信号方向为10°，干扰信号方向为30°。默认快拍数为1024。

图一、图二是在默认设置下的两次实验，可以看到由于每个快拍的信号都存在一定的随机性，算法计算得到的信号统计特性也会存在一定偏差。导致在同样的实验场景下，算法方向图的增益也存在不同，但基本能够抑制入射的干扰信号。

图三、图四分别将快拍数下降到128，32。在低快拍数情况下算法对阵列的协方差矩阵计算的偏差更大。对应地，在实验结果中，算法对干扰信号方向的抑制明显减弱，并且在其他方向的抑制也在一定程度上下降。

图五在0°，30°两个方向施加干扰，并且将干噪比提升到30dB，可以发现算法对多个干扰入射的情况仍能良好地处理。并且在干扰的功率增大时，算法对其的抑制作用也会相应地增大，以最小化最终的输出功率。

图六使用干扰噪声功率$w^H{R}_{nj}w$代替整体信号功率$w^H{R}_{x}w$进行优化。通过实验可以发现，优化干扰噪声功率$w^H{R}_{nj}w$时，在低快拍数，高干噪比的等诸多情况下能够取得更加良好且稳定的效果。

3.线性约束最小方差波束形成

在MVDR算法的基础上，假如考虑到对入射的干扰信号的约束，问题转化为多个约束条件下的优化问题，形成了LCVM算法，如下式所示：
$$\begin{array}{rl}& \underset{w}{\min }{w}^{H}Rw\\ & \text{ s.t. }\{\begin{array}{l}{w}^{H}a\left({\theta }_d\right)=1\\ w^{H}a\left({\theta }_j\right)=0\end{array}\end{array}$$
通过矩阵形式表示，可以得到：
$$\{\begin{array}{l}{w}_{opt}=\mathrm{argmax}{w}^H{R}_{x}w\\ \text{ s.t. }{C}^{H}w=f\end{array}$$
式中$C$为$M\times P$维的约束矩阵，$f$为$P\times 1$维的向量，并且约束方程组的个数需要少于阵元个数，以保证方程有解。同样通过矩阵微商和拉格朗日乘数法等方法，可以求解这个优化问题，解得：
$$w_{LCMT}=R_x^{-1}C{\left(C^H{R}_x^{-1}C\right)}^{-1}f$$
LCMV算法是MVDR算法的拓展情况，同时，MVDR算法是LMCV算法在只考虑入射信号时的特例，当$C=a({\theta }_d)$且$f=[1]$时，$w_{LCMV}$与$w_{MVDR}$相等。

4.广义旁瓣相消器

为了避免约束性自适应算法，1982 年J. Griffiths 提出了广义旁瓣相消器（General sidelobe canceller，GSC）。

该算法通过两路处理信号，将输入信号分解到约束子空间和非约束子空间。约束子空间由约束条件形成，是由信号和干扰入射方向的导向矢量张成的子空间。当权值向量$w$与某一导向矢量正交($w^{H}a({\theta }_j)=0$)时，对应方向的信号无法对最终输出信号$y$造成影响，该信号被抑制。同样地，可以对某个方向的信号进行一个抽取($w^{H}a({\theta }_d)=1$)。

算法通过调整$w$对应约束空间内的权重，对目标信号进行一个抽取，然后对干扰方向信号进行一个抑制。并且由于约束子空间和非约束子空间之间正交，$w$在约束子空间对应的权重对非约束子空间内的信号值没有影响。

在非约束子空间中，算法再次又变成了一个优化问题，通过改变非约束子空间对应$w$的权值，最小化非约束子空间中输出功率的大小。

对于噪声而言，可以看作M维的随机变量，噪声的一部分投影到约束子空间，一部分投影到非约束子空间。约束子空间内的噪声相应地被抽取或抑制，而非约束子空间内的噪声根据其统计特性，在优化问题中最小化输出功率。

广义旁瓣相消算法流程图

可以证明在纯延时条件下 GSC 是 LCMV 的一种等效实现结构，GSC 结构将 LCMV 的约束优化问题转化为了无约束的优化问题。其中GSC算法的权重可以表示为：
$$w=w_q-B{w}_a$$
最终通过推导可得$w_q={\left(C{C}^H\right)}^{-1}Cf$，$w_a={\left(B^H{R}_{x}B\right)}^{-1}{B}^H{R}_x{w}_q$时，取到最优解。