概率论知识点

基础知识

文章当中的图片截图来自【可能是全网最好的《概率统计》期末速成，2小时不到冲刺60分，概率论与数理统计】

概率的性质

加法公式：

• 对于任意事件A、B，有$P(A\bigcup B)=P(A)+P(B)-P(AB)$
• 对于任意事件A、B、C，有$P(A\bigcup B\bigcup C)=P(A)+P(B)+(C)-P(AB)-P(BC)-P(AC)+P(ABC)$
• 若A、B、C互不相容，则$P(A\bigcup B\bigcup C)=P(A)+P(B)+P(C)$

减法公式：

• 对于事件A、B，有$P(A-B)=P(A)-P(AB)$
• 若$B\subset A$，则有$P(B)\le P(A)$，且$P(A-B)=P(A)-P(B)$

对立事件概率：

• $P(\overline{A})=1-P(A)$

分配律：

• P { ( A ⋃ B ) ⋂ C } = P { A C ⋃ B C } P\{(A\bigcup{B})\bigcap{C}\}=P\{AC\bigcup{BC}\} P{(A⋃B)⋂C}=P{AC⋃BC}
• $P\{(AB)\bigcup C\}=P\{(A\bigcup C)\bigcap (B\bigcup C)\}$

对偶率：

• P { A ⋃ B ‾ } = P { A ‾ ⋂ B ‾ } P\{\overline{A\bigcup{B}}\}=P\{\overline{A}\bigcap{\overline{B}}\} P{A⋃B​}=P{A⋂B}
• P { A ⋂ B ‾ } = P { A ‾ ⋃ B ‾ } P\{\overline{A\bigcap{B}}\}=P\{\overline{A}\bigcup{\overline{B}}\} P{A⋂B​}=P{A⋃B}

条件概率

事件A发生的条件下，B发生的概率为$P(B|A)=\frac{P(AB)}{P(A)}$

若$P(A)>0$，则$P(AB)=P(B|A)P(A)$

性质：

• $P(\overline{B}|A)=1-P(B|A)=1-\frac{P(AB)}{P(A)}$
• $P(B\bigcup C|A)=P(B|A)+P(C|A)-P(BC|A)$

古典概型

若随机试验的样本空间$\Omega$只有有限个样本点，且每个基本事件发生的可能性相等，则事件A发生的概率为
$$\begin{gathered} P(A)=\frac{A中所含样本点k}{\Omega 中所有样本点数n}=\frac{k}{n} \\ {C}_n^m=\frac{n!}{m!(n-m)!}=C_7^4=\frac{7\times 6\times 5\times 4\times 3\times 2\times 1}{4\times 3\times 2\times 1\times 3\times 2\times 1} \end{gathered}$$

全概率与贝叶斯公式

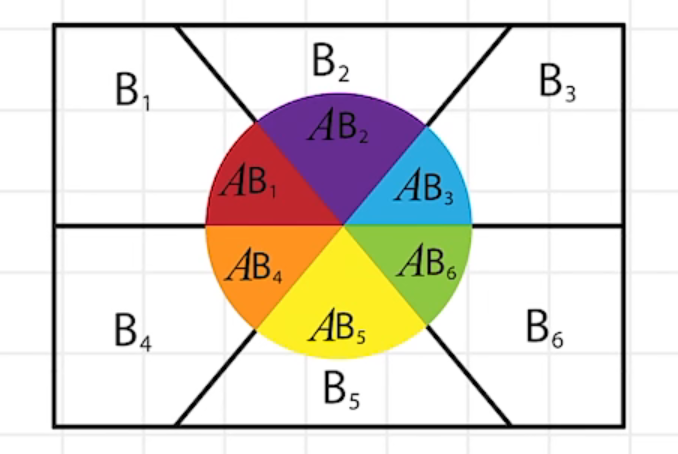
全概率公式：
$$\begin{gathered} P(A)=\sum _{i=1}^{n}P(A{B}_i)=\sum _{i=1}^{n}P(A|B_i)P(B_i) \\ 当所求事件A可以分成几种情况时，A发生的概率就是这些情况对应的概率之和 \end{gathered}$$
贝叶斯公式：
$$\begin{gathered} P(B_i|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(A|B_i)P(B_i)}{{\sum }_{j=1}^{n}P(A|B_j)P(B_j)} \\ 如果A事件发生，判断是发生在哪个情况的时候，用贝叶斯公式 \end{gathered}$$

事件的独立性

• A和B独立
  $$\begin{gathered} P(AB)=P(A)\ast P(B) \\ P(B)=P(B|A)(P(A)>0) \\ P(B|A)=P(B|\overline{A})(0<P(A)<1) \end{gathered}$$

• A和B相互独立，则A和$\overline{B}$，$\overline{A}$和B，

• $\overline{A}$和$\overline{B}$也相互独立

• 若三个事件相互独立，则任意两个事件均满足上述性质；三个事件同时满足$P(ABC)=P(A)P(B)P(C)$

离散型随机变量分布律与分布函数

名称	定义	性质
分布律	$P(X=x_k)=p_k(k=1,2,\cdots )$	$$\begin{gathered} p_k\ge 0,k=1,2,\cdots \\ \sum p_k=1 \end{gathered}$$
分布函数	$F(x)=P(X\le x)={\sum }_{x_k\le x}{p}_k$	$$\begin{gathered} 0\le F(x)\le 1 \\ F(x)单调，不减 \\ F(x)定义域左闭右开 \end{gathered}$$
概率	$P(X\le a)=F(a)$	$$\begin{gathered} P(X>a)=1-F(a) \\ P(a<X\le b)=F(b)-F(a) \end{gathered}$$

二项分布和泊松分布

名称	符号	分布律	含义
二项分布	$B(n,p)$	P { X = k } = C n k p k q n − k ,   ( q = 1 − p , k = 0 , 1 , 2 , ⋯   ) P\{X=k\}=C_{n}^{k}{p^{k}q^{n-k}},\space(q=1-p,k=0,1,2,\cdots) P{X=k}=Cnk​pkqn−k, (q=1−p,k=0,1,2,⋯)	n表示伯努利试验中A发生的次数$X\sim B(n,p)$，$p$表示每次试验中A发生的概率。
泊松分布	$P(\lambda )$	P { X = k } = λ k e − λ k ! , ( λ > 0 , k = 0 , 1 , 2 , ⋯   ) P\{X=k\}=\frac{\lambda^{k}e^{-\lambda}}{k!},(\lambda>0,k=0,1,2,\cdots) P{X=k}=k!λke−λ​,(λ>0,k=0,1,2,⋯)	若$X\sim B(n,p)$，当$n$较大，$p$较小时，$X$近似服从$P(np)$

连续型随机变量分布函数的分布

名称	定义	性质
分布函数	$F(x)=P(X\le x)={\int }_{-\infty }^{x}f(t)dt$	$$\begin{gathered} 0\le F(x)\le 1 \\ F(x)单调，不减 \\ F(x)定义域左闭右开 \end{gathered}$$
概率密度	$f(x),-\infty <x<+\infty$	$$\begin{gathered} f(x)\ge 0 \\ {\int }_{-\infty }^{+\infty }f(x)dx=1 \\ 若f(x)连续，则F\prime (x)=f(x) \end{gathered}$$
概率	$P(X)\le a=F(a)$	$$\begin{gathered} P(X=a)=0 \\ P(X<a)=P(X\le a)=1-F(a) \\ P(a<X\le b)=P(a\le X\le b)=P(a<X<b)=F(b)-F(a) \end{gathered}$$

分布函数法

通过给定的$Y=g(X)$和关于$X$的概率密度函数来求关于$Y$的分布函数和概率密度
$$\begin{gathered} 因为关于X的概率密度函数有范围，根据这个范围和Y=g(X)来求出Y的范围 \\ {F}_Y(y)=P(Y\le y)=P(g(X)\le y)=P(X\in G_y)={\int }_{G_y}{f}_X(x)dx \\ 由上式得出，关于Y的分布函数，求导得到概率密度 \end{gathered}$$

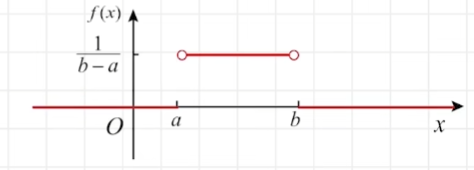
均匀分布

均匀分布$\bigcup (a,b)$的概率密度函数为：
f ( x ) = { 0 , 其他 1 b − a , a < x < b f(x)=\{^{\frac{1}{b-a},a<x<b}_{0,其他} f(x)={0,其他b−a1​,a<x<b​

正态分布

正态分布$N(u,{\sigma }^2)$的概率密度函数为：
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}},(-\infty <x<+\infty )$$

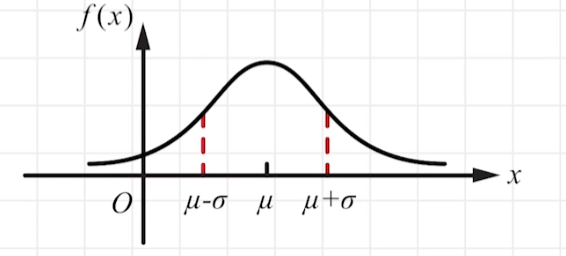
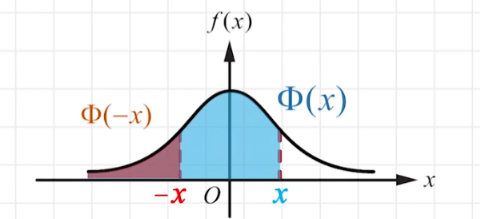
当$\mu =0,\sigma =1$时，称作标准正态分布，记作$N(0,1)$

其分布函数为$\Phi (x)=P(X\le x)$

显然，$\Phi (x)+\Phi (-x)=1$

若$X\sim N(\mu ,{\sigma }^2)$，则$\frac{X-\mu }{\sigma }\sim N(0,1)$

其分布函数可表示为：
$$F(x)=P(X\le x)=P(\frac{X-\mu }{\sigma }\le \frac{x-\mu }{\sigma })=\Phi (\frac{x-\mu }{\sigma })$$

离散型随机变量函数的分布

设$X$为一维离散型随机变量，其分布率为

$X$	$P$
$x_1$	$p_1$
$x_2$	$p_2$
$\cdots$	$\cdots$

那么函数$Y=g(X)$的分布律就是

$g(X)$	$P$
$g(x_1)$	$p_1$
$g(x_2)$	$p_2$
$\cdots$	$\cdots$

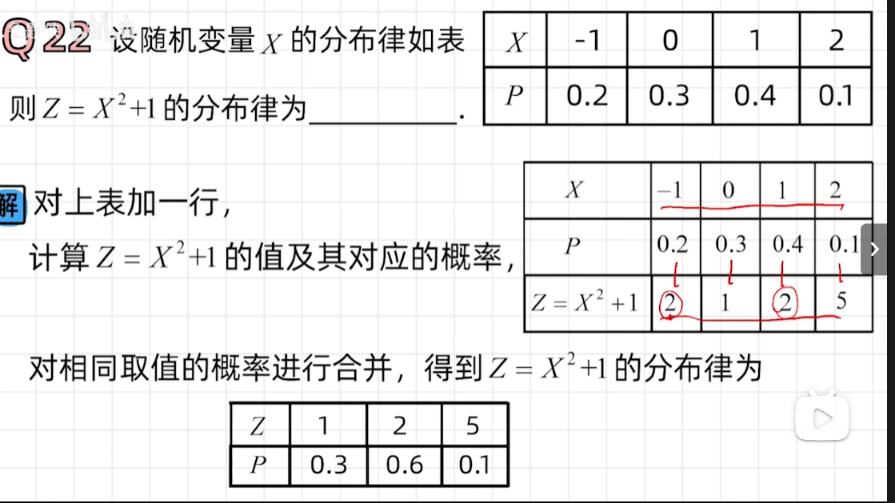
二维离散型随机变量的分布

$X$	$Y$	$P(X_i{Y}_j)$	$P(X=x_i)$	$P(Y=y_j)$
$x_1$	y1	$P_{11}$	$P(x_1)=P_{11}+P_{12}$
$x_1$	$y_2$	$P_{12}$		$P(y_2)=P_{12}+P_{22}$
$x_2$	$y_1$	$P_{21}$		$P(y_1)=P_{11}+P_{21}$
$x_2$	$y_2$	$P_{22}$	$P(x_2)=P_{21}+P_{22}$
$\cdots$	$\cdots$	$P_{\cdots }$	$\sum P(X=x_i)$	$\sum P(Y=y_j)$

$$\begin{gathered} 两者概率总和结果为1 \\ \sum P(X=x_i)+\sum P(Y=y_j)=1 \\ X和Y相互独立要满足，当ij取任意数字只要等于就相互独立 \\ P(X=x_i,Y=y_j)=P(X=x_i)\cdot P(Y=y_j),(任意的i,j=1,2,3,4\cdots ) \end{gathered}$$

二维连续型随机变量的分布

联合分布函数： F ( x , y ) = P { X ≤ x , Y ≤ y } = ∫ − ∞ x ∫ − ∞ y f ( u , v ) d u d v 联合概率密度满足： f ( x , y ) ≥ 0 ; ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 边缘概率密度： f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y ; f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x ; 条件概率密度： f Y ∣ X ( y ∣ x ) = f ( x , y ) f X ( x ) ; f X ∣ Y ( x ∣ y ) = f ( x , y ) f Y ( y ) X 和 Y 相互独立 ⟺ f ( x , y ) = f X ( x ) f Y ( y ) 联合分布函数：F(x,y)=P\{X\leq{x},Y\leq{y}\}=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv\\ 联合概率密度满足：f(x,y)\geq{0};\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dxdy=1\\ 边缘概率密度：f_{X}(x)=\int_{-\infty}^{+\infty}f(x,y)dy;f_{Y}(y)=\int_{-\infty}^{+\infty}f(x,y)dx;\\ 条件概率密度：f_{Y\vert{X}}(y\vert{x})=\frac{f(x,y)}{f_{X}(x)};f_{X\vert{Y}}(x\vert{y})=\frac{f(x,y)}{f_{Y}(y)}\\ X和Y相互独立\Longleftrightarrow{f(x,y)=f_{X}(x)f_{Y}(y)} 联合分布函数：F(x,y)=P{X≤x,Y≤y}=∫−∞x​∫−∞y​f(u,v)dudv联合概率密度满足：f(x,y)≥0;∫−∞+∞​∫−∞+∞​f(x,y)dxdy=1边缘概率密度：fX​(x)=∫−∞+∞​f(x,y)dy;fY​(y)=∫−∞+∞​f(x,y)dx;条件概率密度：fY∣X​(y∣x)=fX​(x)f(x,y)​;fX∣Y​(x∣y)=fY​(y)f(x,y)​X和Y相互独立⟺f(x,y)=fX​(x)fY​(y)

离散型随机变量函数的分布

函数$U=g(X,Y)$的分布律为 P { U = k } = P { g ( X , Y ) = k } P\{U=k\}=P\{g(X,Y)=k\} P{U=k}=P{g(X,Y)=k}

连续型随机变量函数的分布

求$Z=g(X,Y)$的概率密度函数的步骤为：（分布函数法）

1. 先求$Z=g(X,Y)$的分布函数：
   $$F(z)=P(Z\le z)=P(g(X,Y)\le z)=P((X,Y)\in G_z)={\iint }_{G_z}f(x,y)dxdy$$

2. 求导得到$Z$的概率密度函数：$f(z)=F\prime (z)$

若$X,Y$相互独立，其分布函数分别为$F_X(x)$和$F_Y(y)$，则$Z=max(X,Y)$的分布函数为：
$$\begin{array}{rl}{F}_Z(z)=P(max(X,Y)\le z)& =P(X\le z,Y\le z)\\ & =P(X\le z)P(Y\le z)\\ & =F_X(z)F_Y(z)\end{array}$$
若$X,Y$相互独立，其分布函数分别为$F_X(x)$和$F_Y(y)$，则$Z=min(X,Y)$的分布函数为：
$$\begin{array}{rl}{F}_Z(z)=P(min(X,Y)\le z)& =1-P(min(X,Y)>z)\\ & =1-P(X>z,Y>z)\\ & =1-P(X>z)P(Y>z)\\ & =1-[1-F_X(z)][1-F_Y(z)]\end{array}$$
正态分布的可加性：设$X\sim N(\mu ,{\sigma }_1^2),X\sim N({\mu }_2,{\sigma }_2^2)$，且$X,Y$相互独立，则$X+Y\sim N({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$

数学期望

离散型随机变量的期望：$E(X)={\sum }_{i=1}^{\infty }{x}_i{p}_i$

连续型随机变量的期望：$E(X)={\int }_{-\infty }^{+\infty }xf(x)dx$

期望的性质：

• $E(C)=C$，$C$为常数
• $E(CX)=CE(X)$，$C$为常数
• $E(X+Y)=E(X)+E(Y)$
• 设$X,Y$相互独立，则$E(XY)=E(X)E(Y)$

方差和标准差

方差：$D(X)=E[X-E(X){]}^2=E(X^2)-[E(X){]}^2$

标准差：$\sigma =\sqrt{D(X)}$

性质：

• $D(C)=0$，$C$为常数
• $D(X+C)=D(X)$，$C$为常数
• $D(CX)=C^{2}E(X)$，$C$为常数
• $D(X\pm Y)=D(X)+D(Y)\pm 2E\{[X-E(X)][Y-E(Y)]\}$
• 设$X,Y$相互独立，则$D(X\pm Y)=D(X)+D(Y)$

常用的分布的期望和方差

分布	分布律或概率密度	数学期望	方差
0-1分布	P { x = k } = p k ( 1 − p ) 1 − k , ( k = 0 , 1 ) P\{x=k\}=p^{k}(1-p)^{1-k},(k=0,1) P{x=k}=pk(1−p)1−k,(k=0,1)	$p$	$p(1-p)$
二项分布$B(n,p)$	P { x = k } = C n k p k ( 1 − p ) 1 − k P\{x=k\}=C_{n}^{k}{p^{k}(1-p)^{1-k}} P{x=k}=Cnk​pk(1−p)1−k	$np$	$np(1-p)$
泊松分布$P(\lambda )$	P { x = k } = λ k e − λ k ! P\{x=k\}=\frac{\lambda^{k}e^{-\lambda}}{k!} P{x=k}=k!λke−λ​	$\lambda$	$\lambda$
均匀分布$U(a,b)$	$f(x)=\frac{1}{b-a},(a<x<b)$	$\frac{a+b}{2}$	$\frac{(b-a{)}^2}{12}$
正态分布$N(\mu ,{\sigma }^2)$	$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{(x-\mu {)}^2}{2{\sigma }^2}}$	$\mu$	${\sigma }^2$
指数分布$E(\theta )$	$f(x)=\{\begin{array}{l}\theta e^{-\theta x},x>0\\ 0,其他\end{array}$	$\frac{1}{\theta }$	$\frac{1}{{\theta }^2}$

协方差和相关系数

协方差：$Cov(X,Y)=E(XY)-E(X)E(Y)$

协方差的性质：

• $Cov(X,C)=0$，$C$为常数
• $Cov(aX,bY)=abCov(X,Y)$，$a,b$为常数
• $Cov(X_1+X_2,Y)=Cove(X_1,Y)+Cov(X_2,Y)$
• $D(X\pm Y)=D(X)+D(Y)\pm 2Cov(X,Y)$
• 若$X$与$Y$相互独立，则$Cov(X,Y)=0$

相关系数：${\rho }_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\cdot \sqrt{D(Y)}}$

中心极限定理

设随即变量$X_1,X_2,\cdots$独立同分布，$E(X_k)=\mu$，$D(X_k)={\sigma }^2\ne 0,(k=1,2,\cdots )$，则当$n$充分大时，近似有${\sum }_{k=1}^n{X}_k\sim N(n\mu ,n{\sigma }^2)$，即$\frac{{\sum }_{k=1}^n{X}_k-n\mu }{\sqrt{n}\sigma }\sim N(0,1)$

设随机变量$X\sim B(n,p)$，则当$n$充分大时，近似有$X\sim N(np，npq)$，即$\frac{X-np}{\sqrt{npq}}\sim N(0,1)$

三大分布

$X^2(n)$分布：

若$X_1,X_2,\cdots ,X_n$相互独立，且$X_i\sim N(0,1),(i=1,2,\cdots )$，则$X_1^2,X_2^2,\cdots ,X_n^2\sim X^2(n)$

$t(n)$分布：

设$X\sim N(0,1),Y\sim X^2(n)$，$X,Y$相互独立，则称$T=\frac{X}{\sqrt{Y/n}}\sim t(n)$

$F$分布：

设$X\sim X_1^2(n_1),Y\sim X_2^2(n_2)$，$X,Y$相互独立，则$F=\frac{X/n_1}{Y/n_2}\sim F(n_1,n_2)$

矩估计

求解步骤：

1. 写出总体一阶矩$E(X)=g(\theta )$，和样本一阶矩$\overline{X}={\sum }_{i=1}^n{X}_i/n$
2. 令总体矩=样本矩，即$g(\theta )=\overline{X}$，反解出估计量$\hat{\theta }=h(\overline{X})$
3. 将$\overline{X}$具体值代入$\hat{\theta }=h(\overline{X})$，得到估计值

无偏估计：如果$E(\hat{\theta })=\theta$，则称$\hat{\theta }$为$\theta$的无偏估计量。

极大似然估计

离散型总体的最大似然估计步骤

1. 设离散性总体$X$的分布律为 P { X = x } = p ( X , θ ) P\{X=x\}=p(X,\theta) P{X=x}=p(X,θ)，其中$\theta$为未知参数，设$x_1,x_2,\cdots ,x_n$是一组样本观测值
2. 计算似然函数$L(\theta )={\prod }_{i=1}^{n}p(x_i,\theta )$
3. 对似然函数取对数得到$lnL(\theta )={\sum }_{i=1}^{n}lnp(x_i,\theta )$
4. 令$\frac{d}{d\theta }lnL(\theta )=0$，解出最大似然估计$\hat{\theta }$

连续型总体的最大似然估计步骤

1. 设连续性总体$X$的分布律为$f(x,\theta )$，其中$\theta$为未知参数，设$x_1,x_2,\cdots ,x_n$是一组样本观测值
2. 计算似然函数$L(\theta )={\prod }_{i=1}^{n}f(x_i,\theta )$
3. 对似然函数取对数得到$lnL(\theta )={\sum }_{i=1}^{n}lnf(x_i,\theta )$
4. 令$\frac{d}{d\theta }lnL(\theta )=0$，解出最大似然估计$\hat{\theta }$

假设检验

假设检验的步骤

1. 根据题意构造原假设$H_0$和它的对立假设$H_1$
2. 按照下表构造检验统计量
3. 给定显著性水平$\alpha$，写出拒绝域
4. 带入样本观察值，算出统计量的具体值
   • 如果该值落入拒绝域，则拒绝原假设
   • 否则接受原假设

检验参数	检验参数	原假设与备择假设	计算统计量的值	拒绝域W
均值$\mu$	${\sigma }^2$已知	$H_0:\mu ={\mu }_0{H}_1:\mu \ne {\mu }_0$	$z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$|z|>u_{1-\frac{\alpha }{2}}$
均值$\mu$	${\sigma }^2$已知	$H_0:\mu ={\mu }_0{H}_1:\mu >{\mu }_0$	$z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$z>u_{1-\alpha }$
均值$\mu$	${\sigma }^2$已知	$H_0:\mu ={\mu }_0{H}_1:\mu <{\mu }_0$	$z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$	$z<-u_{1-\alpha }$
均值$\mu$	${\sigma }^2$未知	$H_0:\mu ={\mu }_0{H}_1:\mu \ne {\mu }_0$	$t=\frac{\overline{X}-{\mu }_0}{S/\sqrt{n}}$	$|t|<t_{1-\frac{\alpha }{2}}(n-1)$
均值$\mu$	${\sigma }^2$未知	$H_0:\mu ={\mu }_0{H}_1:\mu >{\mu }_0$	$t=\frac{\overline{X}-{\mu }_0}{S/\sqrt{n}}$	$t>-t_{1-a}(n-1)$
均值$\mu$	${\sigma }^2$未知	$H_0:\mu ={\mu }_0{H}_1:\mu <{\mu }_0$	$t=\frac{\overline{X}-{\mu }_0}{S/\sqrt{n}}$	$t<-t_{1-a}(n-1)$

$u_{\alpha }$是标准正态分布的$\alpha$分位数；$t_{\alpha }(n-1)$是自由度为$n-1$的$t$分布的$\alpha$分位数

检验参数	检验参数	原假设与备择假设	计算统计量的值	拒绝域W
方差${\sigma }^2$	$\mu$已知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2\ne {\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\mu {)}^2}{{\sigma }_0^2}$	$X^2<X_{\frac{\alpha }{x}}^2(n)或X^2>X_{1-\frac{\alpha }{2}}^2(n)$
方差${\sigma }^2$	$\mu$已知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2>{\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\mu {)}^2}{{\sigma }_0^2}$	$X^2>X_{1-\alpha }^2(n)$
方差${\sigma }^2$	$\mu$已知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2<{\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\mu {)}^2}{{\sigma }_0^2}$	$X^2<X_{\alpha }^2(n)$
方差${\sigma }^2$	$\mu$未知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2\ne {\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\overline{X}{)}^2}{{\sigma }_0^2}$	$X^2<X_{\frac{\alpha }{x}}^2(n-1)或X^2>X_{1-\frac{\alpha }{2}}^2(n-1)$
方差${\sigma }^2$	$\mu$未知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2>{\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\overline{X}{)}^2}{{\sigma }_0^2}$	$X^2>X_{1-\alpha }^2(n-1)$
方差${\sigma }^2$	$\mu$未知	$H_0:{\sigma }^2={\sigma }_0^2{H}_1:{\sigma }^2<{\sigma }_0^2$	$X^2=\frac{{\sum }_{i=1}^n(X_i-\overline{X}{)}^2}{{\sigma }_0^2}$	$X^2<X_{\alpha }^2(n-1)$

$X_{\alpha }^2(n)$是自由度为$n$的$X^2$分布的$\alpha$分位数