线段树

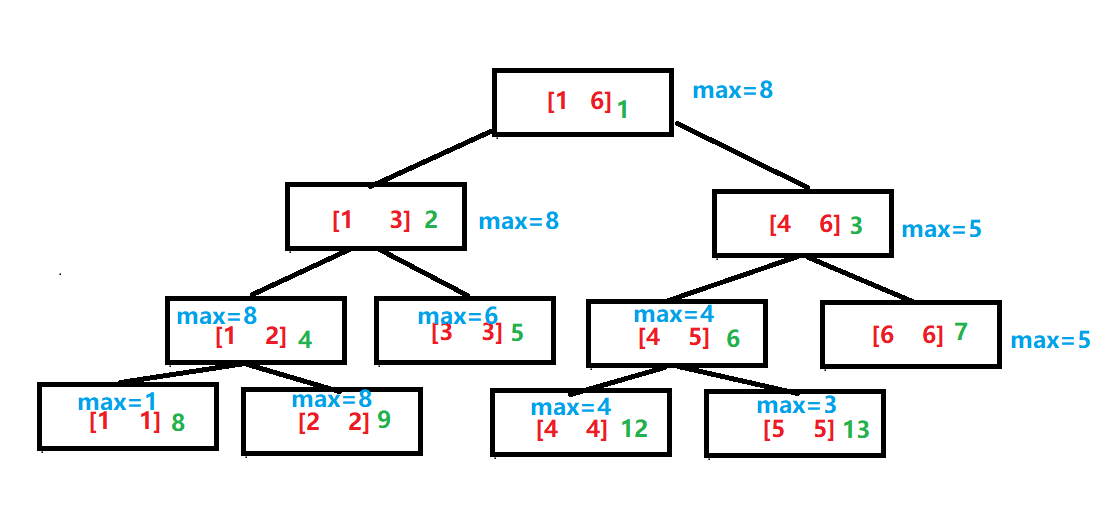
线段树

1.算法分析

1. 一般还要开4N的数组
2. 一般做单点修改、区间查询，加上懒标记后，可以做区间修改、区间查询

可以处理：区间加、区间乘、区间max/min、区间覆盖、区间染色、区间合并、区间开根号、扫描线等问题

2.板子

2.1 单点修改+区间查询

// 该板子是求区间和
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 5e5 + 10;
LL dat[N << 2];  // 4倍空间
int n, m, a[N];

// 上传操作
void pushup(int rt) { 
    dat[rt] = dat[rt << 1] + dat[rt << 1 | 1];
}

// 建树
void build (int rt, int l, int r) {
    if (l == r) {  // 如果当前到达叶节点，那么赋值
        dat[rt] = a[l];  // 赋值是a[l],表示那个叶节点
        return ;
    }
    int mid = (l + r) >> 1;  
    // 递归建立左右子树
    build(rt << 1, l, mid);  
    build(rt << 1 | 1, mid + 1, r);
    // 上传
    pushup(rt);
}

// 单点修改
void modify (int rt, int l, int r, int x, int y) {
    if (l == x && r == x) {  // 递归到叶节点且叶节点刚好为x节点
        dat[rt] += y;  // 修改
        return;
    }
    int mid = (l + r) >> 1;  
    if (x <= mid) modify(rt << 1, l, mid, x, y);  // 如果在左子树 
    else modify(rt << 1 | 1, mid + 1, r, x, y);  // 不在左子树，比在右子树
    pushup(rt);  // 上传
}

// 区间查询
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt];  // 如果当前rt管辖的点能够被[L, R]完全包含，返回
    int mid = (l + r) >> 1;
    LL res = 0;
    if (L <= mid) res += query(rt << 1, l, mid, L, R);  // 如果和左子树有关
    if (mid < R) res += query(rt << 1 | 1, mid + 1, r, L, R);  // 如果可能和右子树有关
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    build(1, 1, n);  // 建树
    for (int i = 1, op, x, y; i <= m; ++i) {
        scanf("%d%d%d", &op, &x, &y);  
        if (op == 1) modify(1, 1, n, x, y);  // 单点修改a[x]+=y
        else printf("%lld\n", query(1, 1, n, x, y));  // 区间查询，求[x, y]的区间和
    }
    return 0;
}

2.2 区间修改+区间查询

// 该板子是求区间和
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int const N = 5e5 + 10;
LL dat[N << 2], lazy[N << 2];
int a[N], n, m;

// 上传标记，每次左右子树建树/区间修改完都需要上传
void pushup(int rt) {
    dat[rt] = dat[rt << 1] + dat[rt << 1 | 1]; 
}

// 建树
void build(int rt, int l, int r) {
    if (l == r) {  // 递归到叶节点
        dat[rt] = a[l];
        lazy[rt] = 0;
        return;
    }
    // 递归建立左右子树
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);  
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);  // 上传
}

// 下传，下传标记，同时改变dat数组
void pushdown(int rt, int l, int r) {
    if (lazy[rt]) {  // 如果有标记
        int mid = (l + r) >> 1;
        
        // 把标记给左右子树
        lazy[rt << 1] += lazy[rt];  
        lazy[rt << 1 | 1] += lazy[rt];
        
        // 改变dat
        dat[rt << 1] += (mid - l + 1) * lazy[rt];
        dat[rt << 1 | 1] += (r - mid) * lazy[rt];
        
        // rt标记清空
        lazy[rt] = 0;
    }
    return;
}

// 区间修改: [L, R] += x
void modify(int rt, int l, int r, int L, int R, int x) {
    if (L <= l && r <= R) {  // 如果当前区间被完全包含
        dat[rt] += (r - l + 1) * x;  // 修改当前区间的dat值
        lazy[rt] += x;  // 改变懒标记
        return ;
    }
    
    pushdown(rt, l, r);  // 下传
    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, x);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, x);
    pushup(rt);  // 上传
    return;
}

// 区间查询:获得[L, R]的区间和
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt];  // 如果[l, r]被完全包含于[L, R]
    pushdown(rt, l, r);  // 标记下传
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    LL res = 0;
    if (L <= mid) res += query(rt << 1, l, mid, L, R);
    if (mid < R) res += query(rt << 1 | 1, mid + 1, r, L, R);
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);  // 读入数组
    build(1, 1, n);  // 建树
    for (int i = 1, a, b, x, op; i <= m; ++i) {
        scanf("%d", &op);
        if (op == 1) {
            scanf("%d%d%d", &a, &b, &x);
            modify(1, 1, n, a, b, x);  // 区间修改, [a, b] += x
        }
        else {
            scanf("%d%d", &a, &b);
            printf("%lld\n", query(1, 1, n, a, b));  // 区间查询，查询[a, b]的区间和
        }
    }
    return 0;
}

2.3 区间加乘操作

// 加乘模板
// x点原来的乘、加法标记为:mul1、add1，后来要加上的乘、加法标记为:mul2、add2
// 可以证明先乘后加最优方法
// x的值变为: x.dat => (x.dat * mul2) + (x.r - x.l + 1) * add2;
// x的乘法标记变为: x.mul1 => x.mul1 * mul2
// x的加法标记变为: x.add1 => x.add1 * mul2 + add2
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 1e5 + 10;
LL dat[N << 2], mul[N << 2], add[N << 2];
int n, p, a[N], m;

// 上传，根的值为左子树的值和右子树的值之和
void pushup(int rt) {
    dat[rt] = (dat[rt << 1] + dat[rt << 1 | 1]) % p;
}

// 建树
void build(int rt, int l, int r) {
    if (l == r) {  // 如果是叶子
        dat[rt] = a[l] % p;
        add[rt] = 0;
        mul[rt] = 1;
        return;
    }
    
    // 如果不是叶子，那么乘法标记必须为1，加法标记为0
    mul[rt] = 1;
    add[rt] = 0;
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid), build(rt << 1 | 1, mid + 1, r);  // 建立左子树和右子树
    pushup(rt);
}

// 加乘的结果
void eval(int rt, int l, int r, LL add2, LL mul2) {
    dat[rt] = ((dat[rt] * mul2 % p) + ((r - l + 1) % p) * add2 % p) % p;
    mul[rt] = mul[rt] * mul2 % p;
    add[rt] = (add[rt] * mul2 % p + add2) % p;
}

// 标记下移
void pushdown(int rt, int l, int r) {
    int mid = (l + r) >> 1;
    eval(rt << 1, l, mid, add[rt], mul[rt]), eval(rt << 1 | 1, mid + 1, r, add[rt], mul[rt]);  // 左右子树分别得到根的标记
    add[rt] = 0, mul[rt] = 1;  // 清空根的标记
    return;
}

// 区间修改
void modify(int rt, int l, int r, int L, int R, LL add2, LL mul2) {
    if (L <= l && r <= R) {  // 如果[L, R]在[l, r]内，直接修改
        eval(rt, l, r, add2, mul2);
        return;
    }
    pushdown(rt, l, r);  // 如果不在[l, r]内，那么分裂，首先要把标记下移
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, add2, mul2);  // 修改左子树
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, add2, mul2);  // 修改右子树
    pushup(rt);  // 修改完子树需要把标记上移
    return;
}

// 询问区间和[L, R]
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt] % p;
    pushdown(rt, l, r);  // 如果[L, R]不在[l, r]内，那么需要分裂，首先要把标记下移
    LL res = 0;
    int mid = (l + r) >> 1;
    if (L <= mid) res = query(rt << 1, l, mid, L, R) % p;  // 左子树
    if (mid < R) res = (res + query(rt << 1 | 1, mid + 1, r, L, R) % p) % p;  // 右子树
    return res;
}

int main() {
    cin >> n >> p;  // 输入数字的个数和模数
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);  // 输入数字
    build(1, 1, n);  // 建树
    cin >> m;  // 输入操作数
    for (int i = 1, op, t, g, c; i <= m; ++i) {  // 输入每次的具体操作
        scanf("%d", &op);
        if (op == 1) {  // 区间乘
            scanf("%d%d%d", &t, &g, &c);
            modify(1, 1, n, t, g, 0, c);
        }
        else if (op == 2) {  // 区间加
            scanf("%d%d%d", &t, &g, &c);
            modify(1, 1, n, t, g, c, 1);
        }
        else {  // 询问区间和
            scanf("%d%d", &t, &g);
            cout << query(1, 1, n, t, g) << endl;
        }
    }
    return 0;
}

2.4 区间染色

2.4.1 有限染色问题

/*本题是区间覆盖问题，求指定区间内有多少的颜色数目，因为颜色的数目比较少，因此
可以使用一个int整数来表示所有的颜色数目，而后就是线段树的常规操作*/
#include <bits/stdc++.h>

using namespace std;

int const N = 1e5 + 10;
typedef long long LL;

LL add[N << 2], sum[N << 2];  // add为记录颜色的懒标记，sum为当前区间的颜色

// 向下传递操作
void pushup(int u) {
    sum[u] = sum[u << 1] | sum[u << 1 | 1];  // 当前颜色由子区间颜色得到
}

// 向上传递操作
void pushdown(int u) {
    if (add[u]) {  // 如果当前u节点有颜色的话

        // 给左右子节点标记都赋值
        add[u << 1] = add[u];  
        add[u << 1 | 1] = add[u];

        // 给左右节点的sum赋值，记录颜色
        sum[u << 1] = add[u];
        sum[u << 1 | 1] = add[u];

        // 去掉懒标记
        add[u] = 0;
    }
}

// 建树
void build(int u, int l, int r) {
    add[u] = 0;  // 初始每个节点都没有懒标记
    if (l == r) {  // 如果递归到叶节点
        sum[u] = 1;  // 叶节点的颜色赋值
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid);  // 建立左右子树
    build(u << 1| 1, mid + 1, r);
    pushup(u);  // 标记上传
}

// 区间赋值操作
void modify(int u, int l, int r, int c, int L, int R) {
    if (L <= l && r <= R) {  // 如果[l, r]完全被包含在要赋值的区间[L, R]的话，那么直接修改
        add[u] = 1 << (c - 1);
        sum[u] = 1 << (c - 1);
        return;
    }
    pushdown(u);  // 下传标记，因为因为标记要分裂
    int mid = l + r >> 1;
    if (L <= mid) modify(u << 1, l, mid, c, L, R);  // 递归修改左右子树
    if (mid < R) modify(u << 1 | 1, mid + 1, r, c, L, R);
    pushup(u);  // 上传操作
}

// 区间查询多少个颜色
LL query(int u, int l, int r, int L, int R) {
    if (L <= l && r <= R) return sum[u];  // 如果[l, r]完全被包含在要赋值的区间[L, R]的话，那么返回
    pushdown(u);  // 标记下移
    int mid = l + r >> 1;
    LL res = 0;

    // 递归查询左右子树
    if (L <= mid) res |= query(u << 1, l, mid, L, R);
    if (mid < R) res |= query(u << 1 | 1, mid + 1, r, L, R);
    return res;
}

int main() {
    int L, T, O, a, b, c; 
    cin >> L >> T >> O;  // 读入节点数、颜色总数、操作数
    build(1, 1, L);
    while (O--) {
        char op[2];
        scanf("%s", op);  // 读入操作类型
        if (op[0] == 'P') {
            scanf("%d %d", &a, &b);
            if (a > b) swap(a, b);  // 保证a要比b小
            LL ans = query(1, 1, L, a, b);  // 查询a到b的颜色总数，颜色总数用一个int型数表示
            LL res = 0;  
            while (ans) {  // 记录这个int型数有多少个1
                if (ans & 1) res++;
                ans >>= 1;
            }
            printf("%lld\n", res);
        }
        else {
            scanf("%d%d%d", &a, &b, &c);  // 读入[a, b]和修改为的值
            if (a > b) swap(a, b);
            modify(1, 1, L, c, a, b);  // 修改操作
        }
    }
    return 0;
}

2.4.2 一般染色问题

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <set>

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

int const N = 2e4 + 10;
LL lazy[N << 2];
int a[N], n, m;
vector<int> v;
PII query[N / 2];

void build (int rt, int l, int r) {
    if (l == r) {  // 如果当前到达叶节点，那么赋值
        lazy[rt] = 0;  // 赋值是a[l],表示那个叶节点
        return ;
    }
    int mid = (l + r) >> 1;  
    // 递归建立左右子树
    build(rt << 1, l, mid);  
    build(rt << 1 | 1, mid + 1, r);
}

// 下传，下传标记，同时改变dat数组
void pushdown(int rt, int l, int r) {
    if (lazy[rt]) {  // 如果有标记
        int mid = (l + r) >> 1;

        // 把标记给左右子树
        lazy[rt << 1] = lazy[rt];
        lazy[rt << 1 | 1] = lazy[rt];

        // rt标记清空
        lazy[rt] = 0;
    }
    return;
}

// 单点查询:a[l]
LL Query(int rt, int l, int r, int x) {
    if (l == r) return lazy[rt];  // 如果[l, r]被完全包含于[L, R]
    pushdown(rt, l, r);                     // 标记下传
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    if (x <= mid) return Query(rt << 1, l, mid, x);
    else return Query(rt << 1 | 1, mid + 1, r, x);
}

// 区间修改: [L, R] = x
void modify(int rt, int l, int r, int L, int R, int x) {
    if (L <= l && r <= R) {  // 如果当前区间被完全包含
        lazy[rt] = x;        // 改变懒标记
        return;
    }

    pushdown(rt, l, r);  // 下传
    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, x);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, x);
    return;
}

// 离散化
int getid(int x) { return lower_bound(v.begin(), v.end(), x) - v.begin() + 1; }

int main() {
    int T;
    cin >> T;
    while (T--) {
        v.clear();
        set<int> s;
        cin >> n;

        // 离散化
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d", &query[i].first, &query[i].second);
            v.push_back(query[i].first), v.push_back(query[i].second);
        }
        sort(v.begin(), v.end());
        v.erase((v.begin(), v.end()), v.end());
        int len = v.size();

        // 建树，相当于memset，但是节约了时间
        build(1, 1, len);
        
        // 离散化赋值回去
        for (int i = 1; i <= n; ++i) {
            query[i].first = getid(query[i].first);
            query[i].second = getid(query[i].second);
        }

        // 区间赋值
        for (int i = 1; i <= n; ++i) modify(1, 1, len, query[i].first, query[i].second, i);

        // 计算每个点的颜色
        for (int i = 1; i <= len; ++i) {
            int tmp = Query(1, 1, len, i);
            if (tmp) s.insert(tmp);
        }
        printf("%d\n", s.size());
    }
    return 0;
}

2.5 区间开根号

// 由于数字最大只到long long，因此最多开发8次，那么直接暴力，递归到叶子节点，暴力修改后pushup，然后再普通查询
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int const N = 1e5 + 10;
LL dat[N << 2], a[N];
int n, m, kase = 1;

// 上传标记，每次左右子树建树/区间修改完都需要上传
void pushup(int rt) { dat[rt] = dat[rt << 1] + dat[rt << 1 | 1]; }

// 建树
void build(int rt, int l, int r) {
    if (l == r) {  // 递归到叶节点
        dat[rt] = a[l];
        return;
    }
    // 递归建立左右子树
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);  // 上传
}

// 区间修改: [L, R] 开方
void modify(int rt, int l, int r, int L, int R) {
    if (dat[rt] == r - l + 1) return;  // 如果这个区间全部都为1
    if (l == r) {  // 如果递归到叶子节点，那么直接修改
        dat[rt] = (int)sqrt((double)dat[rt]);
        return;
    }

    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R);
    pushup(rt);  // 上传
    return;
}

// 区间查询:获得[L, R]的区间和
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt];  // 如果[l, r]被完全包含于[L, R]
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    LL res = 0;
    if (L <= mid) res += query(rt << 1, l, mid, L, R);
    if (mid < R) res += query(rt << 1 | 1, mid + 1, r, L, R);
    return res;
}

int main() {
    while (scanf("%d", &n) != EOF) {
        printf("Case #%d:\n", kase++);
        for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);  // 读入数组
        build(1, 1, n);
        cin >> m;
        for (int i = 1, a, b, op; i <= m; ++i) {
            scanf("%d%d%d", &op, &a, &b);
            if (a > b) swap(a, b);
            if (op == 0)
                modify(1, 1, n, a, b);  // 区间修改, [a, b]开方
            else
                printf("%lld\n", query(1, 1, n, a, b));  // 区间查询，查询[a, b]的区间和
        }
        puts("");
    }
    return 0;
}

2.6 区间合并

2.6.1 最大连续子段和

// 求最大连续的子段和
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 3;

int n, m;
typedef long long LL;
LL a[N];
struct node {
    int l, r;
    LL lmax, rmax, sum, tmax;  // lmax维护从左端点开始的最大子段和，rmax维护从右端点开始的最大子段和，sum维护区间和，tmax维护整个区间的最大子段和
} tr[N * 4];

void pushup(node &u, node &a, node &b) {
    u.lmax = max(a.lmax, a.sum + b.lmax);
    u.rmax = max(b.rmax, a.rmax + b.sum);
    u.sum = a.sum + b.sum;
    u.tmax = max(a.tmax, max(b.tmax, a.rmax + b.lmax));
}

void build(int u, int l, int r) {
    tr[u].l = l;
    tr[u].r = r;
    if (l == r) {
        tr[u].lmax = tr[u].rmax = tr[u].sum = tr[u].tmax = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(u * 2, l, mid);
    build(u * 2 + 1, mid + 1, r);
    pushup(tr[u], tr[u * 2], tr[u * 2 + 1]);
}

// 修改a[x] = c
void modify(int u, int x, LL c) {
    if (tr[u].l == tr[u].r) {
        tr[u].lmax = tr[u].rmax = tr[u].sum = tr[u].tmax = c;
        return;
    }
    int mid = (tr[u].l + tr[u].r) / 2;
    if (x <= mid)
        modify(u * 2, x, c);
    else
        modify(u * 2 + 1, x, c);
    pushup(tr[u], tr[u * 2], tr[u * 2 + 1]);
}

// 查询[l, r]的最大子段和
node query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    int mid = (tr[u].l + tr[u].r) / 2;
    if (r <= mid)  return query(u * 2, l, r);
    else {
        if (l > mid) return query(u * 2 + 1, l, r);
        else {
            auto left = query(u * 2, l, r);
            auto right = query(u * 2 + 1, l, r);
            node kn;
            pushup(kn, left, right);
            return kn;
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    build(1, 1, n);
    for (int i = 0; i < m; i++) {
        int op, x, y;
        scanf("%d%d%lld", &op, &x, &y);
        if (op == 1) {  // query
            if (x > y) swap(x, y);
            printf("%lld\n", query(1, x, y).tmax);  // 询问区间最大子段和
        } else {  
            modify(1, x, y);  // 将a[x] = y
        }
    }
    return 0;
}

2.6.2 最大连续区间

// 求最大连续区间长度
#include <bits/stdc++.h>

using namespace std;

int const N = 5e4 + 10;
 // lsum数组记录区间左端点开始的最大连续个数，rsum数组记录区间右端点开始往左的最大的连续个数, sum数组表示该区间最大的连续点的个数。
int sum[N << 2], lsum[N << 2], rsum[N << 2]; 
int a[N];
int n, m, x, tot;

void pushup(int rt, int len) {
    lsum[rt] = lsum[rt << 1];
    rsum[rt] = rsum[rt << 1 | 1];
    if (lsum[rt << 1] == (len - (len >> 1)))
        lsum[rt] = lsum[rt << 1] + lsum[rt << 1 | 1];
    if (rsum[rt << 1 | 1] == (len >> 1))
        rsum[rt] = rsum[rt << 1] + rsum[rt << 1 | 1];
    sum[rt] = max(rsum[1 << 1] + lsum[1 << 1 | 1], max(sum[rt << 1], sum[rt << 1 | 1]));
}

void build(int rt, int l, int r) {
    if (l == r) {
        sum[rt] = lsum[rt] = rsum[rt] = 1;
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt, r - l + 1);
}

// a[pos] = c
void modify(int rt, int l, int r, int pos, int c) {
    if (l == r) {
        sum[rt] = rsum[rt] = lsum[rt] = c;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        modify(rt << 1, l, mid, pos, c);
    else
        modify(rt << 1 | 1, mid + 1, r, pos, c);
    pushup(rt, r - l + 1);
}

// 询问包含x的最长连续区间长度
int query(int rt, int l, int r, int pos) {
    if (l == r) return sum[rt];
    int mid = (l + r) >> 1;
    if (pos <= mid) {
        if (pos + rsum[rt << 1] > mid)
            return rsum[rt << 1] + lsum[rt << 1 | 1];
        else
            return query(rt << 1, l, mid, pos);
    } else {
        if (mid + lsum[rt << 1 | 1] >= pos)
            return lsum[rt << 1 | 1] + rsum[rt << 1];
        else
            return query(rt << 1 | 1, mid + 1, r, pos);
    }
}

int main() {
    char op[10];
    while (scanf("%d%d", &n, &m) != EOF) {
        build(1, 1, n);
        tot = 0;
        while (m--) {
            scanf("%s", op);
            if (op[0] == 'Q') {
                scanf("%d", &x);
                printf("%d\n", query(1, 1, n, x));  // 询问包含x的最长连续区间长度
            } else if (op[0] == 'D') {
                scanf("%d", &x);
                a[++tot] = x;
                modify(1, 1, n, x, 0);  // a[x] = 0
            } else {
                x = a[tot--];
                modify(1, 1, n, x, 1);  // a[x] = 1
            }
        }
    }
    return 0;
}

2.7 区间每个数字的平方和、立方和

/*
	对于一个区间有4个操作：
	1.将a~b都加上c
	2.将a~b都乘上c
	3.将a~b都变成c
	4.查询a~b的每个数的p次方的和。（p=1,2,3）
*/
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
typedef long long LL;
const int p = 10007;
int n, m, r, t;

int a[N], sum1[N * 4], sum2[N * 4], sum3[N * 4], lazy_mul[N * 4], lazy_add[N * 4];  // w[i]=j表示时间戳为i的点的值为j，a[]输入每个节点的值，dat线段树每个点权值，lazy线段树每个点的懒标记

void solve(int rt, int len, int a, int b) {  // a为add b为mul
    // 修改乘法和加法标记
    lazy_mul[rt] = 1ll * lazy_mul[rt] * b % p;
    lazy_add[rt] = 1ll * lazy_add[rt] * b % p;
    lazy_add[rt] = ((lazy_add[rt] + a) % p + p) % p;

    // 先维护乘法标记：x^3=>(bx)^3, x^2=>(bx)^2
    if (b != 1) {  //先乘后加
        sum1[rt] = 1ll * sum1[rt] * b % p;
        sum2[rt] = (1ll * sum2[rt] * b % p) * b % p;
        sum3[rt] = ((1ll * sum3[rt] * b % p) * b % p) * b % p;
    }

    // 再维护加法标记：(x+a)^3=x^3+3x^2*a+3xa^2+a^3, (x+a)^2=x^2+2xa+a^2
    if (a != 0) {
        int a2 = 1ll * a * a % p, a3 = 1ll * a2 * a % p;
        sum3[rt] = ((sum3[rt] + (LL)len * a3 % p) + p) % p;
        sum3[rt] = ((sum3[rt] + 3ll * (LL)sum2[rt] % p * a % p) + p) % p;
        sum3[rt] = ((sum3[rt] + 3ll * (LL)sum1[rt] % p * a2 % p) + p) % p;
        sum2[rt] = ((sum2[rt] + 2ll * (LL)sum1[rt] % p * a % p) + p) % p;
        sum2[rt] = ((sum2[rt] + (LL)len * a2 % p) + p) % p;
        sum1[rt] = ((sum1[rt] + (LL)len * a % p) + p) % p;
    }
}

void pushup(int rt) {
    sum1[rt] = (sum1[rt << 1] + sum1[rt << 1 | 1]) % p;
    sum2[rt] = (sum2[rt << 1] + sum2[rt << 1 | 1]) % p;
    sum3[rt] = (sum3[rt << 1] + sum3[rt << 1 | 1]) % p;
}

// 建线段树，rt为根，l为rt点管辖的左边界， r为rt点管辖的有边界
void build(int rt, int l, int r) {
    lazy_add[rt] = 0;
    lazy_mul[rt] = 1;
    if (l == r) {
        int temp = a[l];
        sum1[rt] = temp;
        sum2[rt] = (1ll * sum1[rt] * sum1[rt]) % p;
        sum3[rt] = (1ll * sum1[rt] * sum2[rt]) % p;
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

// 下传
void pushdown(int rt, int l, int r) {
    int mid = (l + r) >> 1;
    solve(rt << 1, mid - l + 1, lazy_add[rt], lazy_mul[rt]);
    solve(rt << 1 | 1, r - mid, lazy_add[rt], lazy_mul[rt]);
    lazy_add[rt] = 0;
    lazy_mul[rt] = 1;
}

// L为需要修改的左区间，R为需要修改的右区间
void modify(int rt, int l, int r, int L, int R, int a, int b) {
    if (L <= l && r <= R) {
        solve(rt, r - l + 1, a, b);
        return;
    }
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, a, b);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, a, b);
    pushup(rt);
}

// L为需要查询的左区间，R为查询的右区间
int query(int rt, int l, int r, int L, int R, int cnt) {
    if (L <= l && r <= R) {
        if (cnt == 1)
            return sum1[rt];
        else if (cnt == 2)
            return sum2[rt];
        else
            return sum3[rt];
    }
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    int ans = 0;
    if (L <= mid) ans += query(rt << 1, l, mid, L, R, cnt), ans %= p;
    if (mid < R) ans += query(rt << 1 | 1, mid + 1, r, L, R, cnt), ans %= p;
    pushup(rt);
    return ans;
}

int main() {
    while (scanf("%d%d", &n, &m) != EOF) {
        if (!n && !m) break;
        build(1, 1, n);
        // m次询问
        for (int i = 1, op, x, y, z; i <= m; i++) {
            scanf("%d%d%d%d", &op, &x, &y, &z);
            if (op == 1)
                modify(1, 1, n, x, y, z, 1);  // [x, y] += c
            else if (op == 2)
                modify(1, 1, n, x, y, 0, z);  // [x, y] *= c
            else if (op == 3)
                modify(1, 1, n, x, y, z, 0);  // [x, y] = c
            else
                printf("%d\n", query(1, 1, n, x, y, z));  // [x, y] 每个数字的z次方的和
        }
    }
    return 0;
}

2.8 扫描线求矩形面积并

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n;
struct Segment {
    double x, y1, y2;
    int k;
    bool operator<(const Segment &t) const { return x < t.x; }
} seg[N * 2];
int cnt[N << 3];  // cnt[u]维护u的管理区间是否全部都被覆盖
double len[N << 3];  // len[u]维护u的管理区间内覆盖的长度

vector<double> ys;

int find(double y) { return lower_bound(ys.begin(), ys.end(), y) - ys.begin(); }

void pushup(int u, int l, int r) {
    if (cnt[u])  // 如果这段都被覆盖，那么有效的长度就是这段长度
        len[u] = ys[r + 1] - ys[l];
    else if (l != r)  // 如果这段没有完全覆盖，那么就是左子区间被覆盖长度+右子区间被覆盖长度
        len[u] = len[u << 1] + len[u << 1 | 1];
    else  // 要不然就是0
        len[u] = 0;
}

void build(int u, int l, int r) {
    len[u] = cnt[u] = 0;
    if (l != r) {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    }
}

void modify(int u, int l, int r, int L, int R, int k) {
    if (L <= l && r <= R) {
        cnt[u] += k;
        pushup(u, l, r);
    } else {
        int mid = l + r >> 1;
        if (L <= mid) modify(u << 1, l, mid, L, R, k);
        if (mid < R) modify(u << 1 | 1, mid + 1, r, L, R, k);
        pushup(u, l, r);
    }
}

int main() {
    int T = 1;
    while (scanf("%d", &n) != EOF) {
        if (!n) break;
        ys.clear();
        for (int i = 0, j = 0; i < n; i++) {
            double x1, y1, x2, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            seg[j++] = {x1, y1, y2, 1};  // 矩形的左边界+1
            seg[j++] = {x2, y1, y2, -1};  // 右边界减1
            ys.push_back(y1), ys.push_back(y2);  // y离散化
        }

        // 排序去重
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        build(1, 0, ys.size() - 2);

        sort(seg, seg + n * 2);

        double res = 0;
        for (int i = 0; i < n * 2; i++) {
            if (i > 0) res += len[1] * (seg[i].x - seg[i - 1].x);  // 每次都是计算全部长度的len，所以只需要len[1],矩形面积就是len[1]为宽，乘上(x2 - x1)为长
            modify(1, 0, ys.size() - 2, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);  // 把这段都加上k
        }

        printf("Test case #%d\n", T++);
        printf("Total explored area: %.2lf\n\n", res);
    }
    return 0;
}

3. 例题

3.1 常规操作题

luogu P1047 校门外的树
题意： 有一个数轴，长度为l+1,从0~l上每个点都种树。现在有m个操作，每个操作输入a和b，表示要把[a, b]上的树砍掉，问m次操作后，数轴上还剩下多少棵树?
题解： 只需要改区间修改+区间查询的板子即可，当砍掉[a,b]上的树时，就算把[a, b]赋值为0，最后统计还剩多少棵树，就算计算[1,n]的区间求和。
代码：

// 该板子是求区间和
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int const N = 5e5 + 10;
LL dat[N << 2], lazy[N << 2];
int a[N], n, m;

// 上传标记，每次左右子树建树/区间修改完都需要上传
void pushup(int rt) {
    dat[rt] = dat[rt << 1] + dat[rt << 1 | 1]; 
}

// 建树
void build(int rt, int l, int r) {
    if (l == r) {  // 递归到叶节点
        dat[rt] = a[l];
        lazy[rt] = 1;
        return;
    }
    lazy[rt] = 1;
    // 递归建立左右子树
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);  
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);  // 上传
}

// 下传，下传标记，同时改变dat数组
void pushdown(int rt, int l, int r) {
    if (lazy[rt] == 0) {  // 如果有标记
        
        // 把标记给左右子树
        lazy[rt << 1] = 0;  
        lazy[rt << 1 | 1] = 0;
        
        // 改变dat
        dat[rt << 1] = 0 ;
        dat[rt << 1 | 1] = 0;
        
        // rt标记清空
        lazy[rt] = 1;
    }
    return;
}

// 区间修改: [L, R] += x
void modify(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) {  // 如果当前区间被完全包含
        dat[rt] = 0;  // 修改当前区间的dat值
        lazy[rt] = 0;  // 改变懒标记
        return ;
    }
    
    if (lazy[rt] == 0) pushdown(rt, l, r);  // 下传
    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R);
    pushup(rt);  // 上传
    return;
}

// 区间查询:获得[L, R]的区间和
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt];  // 如果[l, r]被完全包含于[L, R]
    if (lazy[rt] == 0) pushdown(rt, l, r);  // 标记下传
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    LL res = 0;
    if (L <= mid) res += query(rt << 1, l, mid, L, R);
    if (mid < R) res += query(rt << 1 | 1, mid + 1, r, L, R);
    return res;
}

int main() {
    cin >> n >> m;
    n ++;
    for (int i = 1; i <= n; ++i) a[i] = 1;
    build(1, 1, n);  // 建树
    // cout << query(1, 1, n, 1, n) << endl;
    for (int i = 1, a, b; i <= m; ++i) {
        scanf("%d%d", &a, &b);
        a++, b++;
        modify(1, 1, n, a, b);
    }
    cout << query(1, 1, n, 1, n) << endl;
    return 0;
}

luogu P5057 [CQOI2006]简单题
题意： 有一个 n 个元素的数组，每个元素初始均为 0。有 m 条指令，要么让其中一段连续序列数字反转——0 变 1，1 变 0（操作 1），要么询问某个元素的值（操作 2）。 1 ≤ n ≤ 10⁵, 1 ≤ m ≤ 5 × 10⁵
题解： 线段树维护，每次给定反转区间[a, b]，那么把[a, b]区间中每个数字加1，而后每次询问x的时候，只需要query(1,1,n,x,x)，而后判断这个值是奇数还是偶数，奇数输出1，偶数输出0即可
代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

int const N = 1e5 + 10;
LL dat[N << 2], lazy[N << 2];
int n, m;

// 上传标记，每次左右子树建树/区间修改完都需要上传
void pushup(int rt) {
    dat[rt] = dat[rt << 1] + dat[rt << 1 | 1]; 
}

// 建树
void build(int rt, int l, int r) {
    if (l == r) {  // 递归到叶节点
        dat[rt] = 0;
        lazy[rt] = 0;
        return;
    }
    // 递归建立左右子树
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);  
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);  // 上传
}

// 下传，下传标记，同时改变dat数组
void pushdown(int rt, int l, int r) {
    if (lazy[rt]) {  // 如果有标记
        int mid = (l + r) >> 1;
        
        // 把标记给左右子树
        lazy[rt << 1] += lazy[rt];  
        lazy[rt << 1 | 1] += lazy[rt];
        
        // 改变dat
        dat[rt << 1] += (mid - l + 1) * lazy[rt];
        dat[rt << 1 | 1] += (r - mid) * lazy[rt];
        
        // rt标记清空
        lazy[rt] = 0;
    }
    return;
}

// 区间修改: [L, R] += x
void modify(int rt, int l, int r, int L, int R, int x) {
    if (L <= l && r <= R) {  // 如果当前区间被完全包含
        dat[rt] += (r - l + 1) * x;  // 修改当前区间的dat值
        lazy[rt] += x;  // 改变懒标记
        return ;
    }
    
    pushdown(rt, l, r);  // 下传
    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, x);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, x);
    pushup(rt);  // 上传
    return;
}

// 区间查询:获得[L, R]的区间和
LL query(int rt, int l, int r, int L, int R) {
    if (L <= l && r <= R) return dat[rt];  // 如果[l, r]被完全包含于[L, R]
    pushdown(rt, l, r);  // 标记下传
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    LL res = 0;
    if (L <= mid) res += query(rt << 1, l, mid, L, R);
    if (mid < R) res += query(rt << 1 | 1, mid + 1, r, L, R);
    return res;
}

int main() {
    cin >> n >> m;
    build(1, 1, n);  // 建树
    for (int i = 1, a, b, x, op; i <= m; ++i) {
        scanf("%d", &op);
        if (op == 1) {
            scanf("%d%d", &a, &b);
            modify(1, 1, n, a, b, 1);  // 区间修改, [a, b] += 1
        }
        else {
            scanf("%d", &a);
            printf("%lld\n", (query(1, 1, n, a, a) & 1) == 1);  // 区间查询，查询[a, b]的区间和
        }
    }
    return 0;
}

luogu P4588 [TJOI2018]数学计算
题意： 小豆现在有一个数x，初始值为1.小豆有Q次操作，操作有两种类型:
1 m: x = x * m, 输出x%mod;
2 pos：x= x = x / 第pos次操作所乘的数（保证第pos次操作一定为类型1,对于每一个类型1的操作至多会被除一次）输出x % mod;Q <= 10⁵
题解： 使用线段树维护1~Q这Q个数字的区间乘，如果当前是1类型操作，那么进行单点修改modify(1, 1, n, i, x);如果是2类型操作，那么进行单点修改modify(1, 1, n, pos, 1); 每次输出都是所有的成绩, 即dat[1];
代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 1e5 + 10;
LL dat[N << 2];
int n, p, t;

void pushup(int rt) {
    dat[rt] = dat[rt << 1] * dat[rt << 1 | 1] % p;
}

void build(int rt, int l, int r) {
    if (l == r) {
        dat[rt] = 1;
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid), build(rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

void modify(int rt, int l, int r, int x, int y) {
    if (l == r && l == x) {
        dat[rt] = y;
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) modify(rt << 1, l, mid, x, y);
    else modify(rt << 1 | 1, mid + 1, r, x, y);
    pushup(rt);
}

int main() {
    cin >> t;
    while (t--) {
        cin >> n >> p;
        for (int i = 1; i <= n * 4; ++i) dat[i] = 0;
        build(1, 1, n);
        for (int i = 1, op, x; i <= n; ++i) {
            scanf("%d%d", &op, &x);
            if (op == 1) modify(1, 1, n, i, x % p);
            else modify(1, 1, n, x, 1);
            printf("%lld\n", dat[1] % p);
        }
    }
    return 0;
}

icpc2019上海区域赛 F.A Simple Problem On A Tree

题意： 给定一棵树，维护4个操作：

1 u v w：将u->v路径上的点全部赋值为w

2 u v w：将u->v路径上的点全部加上w

3 u v w：将u->v路径上的点全部乘上w

4 u v：询问u->v路径上的点的立方和

题解： 本题考的就是维护4个操作：区间赋值，区间加，区间乘，区间立方和。难点在于维护立方和，加乘操作就是先乘后加。先树剖，然后dfs序建线段树，然后处理即可。

代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+5;
typedef long long LL;
const int p = 1e9 + 7;
int tot, num;
int n, m, r,t,cases=0;

int w[N], a[N], sum1[N * 4], sum2[N * 4], sum3[N * 4], lazy_mul[N * 4], lazy_add[N * 4]; // w[i]=j表示时间戳为i的点的值为j，a[]输入每个节点的值，dat线段树每个点权值，lazy线段树每个点的懒标记
//int h[N], e[N * 2], ne[N * 2], idx;   // 邻接表数组
int dep[N], dfn[N], wson[N], sz[N], top[N], fa[N]; //  dep深度   dfn搜索序 wson重儿子 size子树大小 top链头  fa父节点
vector<int> mp[N];

// 得到sz, fa, dep, wson数组
void dfs1(int u) {
    dep[u] = dep[fa[u]]+1; 
    sz[u] = 1; 
    for(int i = 0; i<mp[u].size(); i++) {
        int j=mp[u][i]; 
        if(j == fa[u]) continue; 
        fa[j] = u; 
        dfs1(j); 
        sz[u] += sz[j]; 
        if(sz[j] > sz[wson[u]]) wson[u] = j;  // 这里要注意根节点不能设为0，否则根节点的最重链无法更新，始终为0
    }
}

// 得到dfn, top数组 
void dfs2(int u, int nowtop) {
    dfn[u] = ++num; 
    w[num] = a[u]; 
    //以搜索序重排权值
    top[u] = nowtop; 
    if(wson[u]) dfs2(wson[u], nowtop);   // 先搜索重儿子
    for(int i = 0; i<mp[u].size(); i++) {// 然后搜索轻儿子
        int y=mp[u][i]; 
        if(y ==fa[u]||y == wson[u]) continue; 
        dfs2(y, y); 
    }
}

void solve(int rt,int len,int a,int b){   //a为add b为mul
    // 修改乘法和加法标记
    lazy_mul[rt] = 1ll*lazy_mul[rt] * b % p;
    lazy_add[rt] = 1ll*lazy_add[rt] * b % p;
    lazy_add[rt] = ((lazy_add[rt] + a) % p + p) % p;

    // 先维护乘法标记：x^3=>(bx)^3, x^2=>(bx)^2
    if(b!=1){   //先乘后加
        sum1[rt] = 1ll*sum1[rt] * b % p;
        sum2[rt] = (1ll*sum2[rt] * b % p) * b % p;
        sum3[rt] = ((1ll*sum3[rt] * b % p) * b % p) * b % p;
    }

    // 再维护加法标记：(x+a)^3=x^3+3x^2*a+3xa^2+a^3, (x+a)^2=x^2+2xa+a^2
    if(a!=0){
        int a2 = 1ll*a * a % p, a3 = 1ll*a2 * a % p;
        sum3[rt] = ((sum3[rt] + (LL)len * a3 % p) + p) % p;
        sum3[rt] = ((sum3[rt] + 3ll * (LL)sum2[rt] % p * a % p) + p) % p;
        sum3[rt] = ((sum3[rt] + 3ll * (LL)sum1[rt] % p * a2 % p) + p) % p;
        sum2[rt] = ((sum2[rt] + 2ll * (LL)sum1[rt] % p * a % p) + p) % p;
        sum2[rt] = ((sum2[rt] + (LL)len * a2 % p) + p) % p;
        sum1[rt] = ((sum1[rt] + (LL)len * a % p) + p) % p;
    }
}

void pushup(int rt) {
    sum1[rt] = (sum1[rt << 1] + sum1[rt << 1 | 1]) % p;
    sum2[rt] = (sum2[rt << 1] + sum2[rt << 1 | 1]) % p;
    sum3[rt] = (sum3[rt << 1] + sum3[rt << 1 | 1]) % p;
}   

// 建线段树，rt为根，l为rt点管辖的左边界， r为rt点管辖的有边界
void build(int rt, int l, int r) {
    lazy_add[rt] = 0;
    lazy_mul[rt] = 1;
    if(l==r) {
        int temp = w[l];
        sum1[rt] = temp;
        sum2[rt] = (1ll*sum1[rt] * sum1[rt]) % p;
        sum3[rt] = (1ll*sum1[rt] * sum2[rt]) % p;
        return ; 
    }
    int mid=(l + r)>>1; 
    build(rt << 1, l, mid); 
    build(rt << 1 | 1, mid+1, r); 
    pushup(rt);
}

// 下传
void pushdown(int rt, int l, int r) {
    int mid = (l + r) >> 1;
    solve(rt << 1, mid - l + 1, lazy_add[rt], lazy_mul[rt]);
    solve(rt << 1 | 1, r - mid, lazy_add[rt], lazy_mul[rt]);
    lazy_add[rt] = 0;
    lazy_mul[rt] = 1;
}

// rt为根，l为rt点管辖的左边界， r为rt点管辖的有边界， L为需要修改的左区间，R为需要修改的右区间
void modify(int rt, int l, int r, int L, int R, int a,int b) {
    if(L <= l && r <= R) {
        solve(rt, r - l + 1, a, b);
        return ; 
    } 
    pushdown(rt, l, r); 
    int mid = (l + r)>>1; 
    if(L <= mid) modify(rt << 1, l, mid, L, R, a,b); 
    if(mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, a,b); 
    pushup(rt);
}

// rt为根，l为rt点管辖的左边界， r为rt点管辖的有边界， L为需要查询的左区间，R为查询的右区间
int query(int rt, int l, int r, int L, int R) {
    if(L <= l && r <= R) {
        return sum3[rt]; 
    }
    pushdown(rt, l, r); 
    int mid = (l + r)>>1; 
    int ans = 0; 
    if(L <= mid) ans += query(rt << 1, l, mid, L, R), ans %= p; 
    if(mid < R) ans += query(rt << 1 | 1, mid + 1, r, L, R), ans %= p;
    pushup(rt);
    return ans; 
}

// 求树从 x 到 y 结点最短路径上所有节点的值之和
int path_query_Tree(int x, int y) {   
    //两点间的修改
    int ans = 0; 
    while(top[x] != top[y]) {// 把x点和y点整到一条重链上
        if(dep[top[x]] < dep[top[y]]) swap(x, y);   // 让x点为深的那个点
        ans += query(1, 1, n, dfn[top[x]], dfn[x]);   
        ans %= p; 
        x = fa[top[x]];  // x每次跳一条链
    }
    if(dep[x] > dep[y]) swap(x, y);   // 让x成为深度更浅的那个点
    ans += query(1, 1, n, dfn[x], dfn[y]); 
    return ans % p; 
}

// 树上修改 a为add ,b为mul
void path_modify_Tree(int x, int y, int a,int b) {
    //树上两点距离 
    while(top[x] != top[y]) { // 把x点和y点整到一条重链上
        if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x成为对应的头部深度更大的那个点
        modify(1, 1, n, dfn[top[x]], dfn[x], a,b); // 累加x的所有子树和
        x = fa[top[x]]; // x跳到原来x的头部的父节点
    }
    if(dep[x] > dep[y]) swap(x, y);  // 让x成为深度更浅的那个点
    modify(1, 1, n, dfn[x], dfn[y], a,b); 
}

int main() {
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        cases++;
        // 读入边，建树
        for(int i=1; i<=n; ++i) mp[i].clear(),wson[i]=0;
        //memset(h,  -1,  sizeof h);
        num = 0;
        for(int i=1, x, y; i<n; i++) {
            scanf("%d%d", &x, &y);
            mp[x].push_back(y);
            mp[y].push_back(x); 
        }

        for(int i=1; i<=n; i++) scanf("%d", &a[i]); // 读入每个点的权值
        // 两次dfs把树按照重链剖分
        dfs1(1);   // 得到sz, fa, dep, wson数组
        dfs2(1, 1);   // 得到dfn, top数组
        build(1, 1, n); 
        scanf("%d", &m);  
        printf("Case #%d:\n", cases);
        // m次询问
        for(int i=1, op, x, y, z; i<=m; i++) {
            scanf("%d", &op); 
            if(op == 1) {
                scanf("%d%d%d", &x, &y, &z); 
                path_modify_Tree(x, y, z,0); // 将树从 x到 y 结点最短路径上所有节点的值赋值为z
            }
            else if(op == 2) {
                scanf("%d%d%d", &x, &y, &z); 
                path_modify_Tree(x, y, z,1); // 将树从 x到 y 结点最短路径上所有节点的值加上z
            }
            else if(op == 3) {
                scanf("%d%d%d", &x, &y, &z); 
                path_modify_Tree(x, y, 0,z); // 将树从 x到 y 结点最短路径上所有节点的值乘上z
            }
            else {
                scanf("%d%d", &x,&y); 
                printf("%d\n", path_query_Tree(x,y)); 
            }
        }
    } 

    return 0;
}

ZOJ 1610 Count the Colors

题意： 在0-8000长的线段里面，按先后次序依次覆盖颜色，求最后每种颜色有多少段？

题解： 首先是区间染色，然后计算每个点的颜色，最后问题就转换为区间划分问题，按照双指针的模板操作即可。

**代码： **

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

int const N = 8010;
LL lazy[N << 2];
map<int, int> s;
int a[N], n, m;

void build(int rt, int l, int r) {
    if (l == r) {      // 如果当前到达叶节点，那么赋值
        lazy[rt] = 0;  // 赋值是a[l],表示那个叶节点
        return;
    }
    int mid = (l + r) >> 1;
    // 递归建立左右子树
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
}

// 下传，下传标记，同时改变dat数组
void pushdown(int rt, int l, int r) {
    if (lazy[rt]) {  // 如果有标记
        int mid = (l + r) >> 1;

        // 把标记给左右子树
        lazy[rt << 1] = lazy[rt];
        lazy[rt << 1 | 1] = lazy[rt];

        // rt标记清空
        lazy[rt] = 0;
    }
    return;
}

// 单点查询:a[l]
LL Query(int rt, int l, int r, int x) {
    if (l == r) return lazy[rt];  // 如果[l, r]被完全包含于[L, R]
    pushdown(rt, l, r);           // 标记下传
    // 递归加上左右子树
    int mid = (l + r) >> 1;
    if (x <= mid)
        return Query(rt << 1, l, mid, x);
    else
        return Query(rt << 1 | 1, mid + 1, r, x);
}

// 区间修改: [L, R] = x
void modify(int rt, int l, int r, int L, int R, int x) {
    if (L <= l && r <= R) {  // 如果当前区间被完全包含
        lazy[rt] = x;        // 改变懒标记
        return;
    }

    pushdown(rt, l, r);  // 下传
    // 递归左右子树修改区间
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, x);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, x);
    return;
}

int main() {
    while (scanf("%d", &n) != EOF) {
        memset(lazy, 0, sizeof lazy);
        memset(a, 0, sizeof a);
        s.clear();
        build(1, 1, N);

        int maxv = 0;
        for (int i = 1; i <= n; ++i) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            a++, b++, c++;
            maxv = max(maxv, b);
            modify(1, 1, N, a, b - 1, c);
        }

        // 计算每个点的颜色
        for (int i = 1; i <= maxv - 1; ++i) {
            int tmp = Query(1, 1, N, i);
            a[i] = tmp;
        }

        // 统计每个分段的颜色
        for (int i = 1, j = 1; i <= maxv - 1; i = j) {
            j = i;
            while (j <= maxv && a[i] == a[j]) j++;
            if (a[i]) s[a[i]]++;
        }
        for (auto si : s) printf("%d %d\n", si.first - 1, si.second);
        printf("\n");
    }
    return 0;
}

HDU 4553 约会安排

这个大佬讲的很明白了，代码好多，想想就多不想写了：https://blog.csdn.net/laaahu/article/details/103170252

题意： 一个人拥有T的总时间， 和M件要做的事情。
三种事情：
一是屌丝基友约他出去玩， 他如果在某个时间段内有一段连续时间就和基友出去玩，相应的那段时间将会被占用。
二是女神约她出去， 他会在自己的安排结束的时间段内去找一段连续时间和女神去约会，相应的这段时间也被占用将不再被后面的事情使用。如果在这段时间里没有找到他就会去，找已经被基友占的时间，会选择放基友的鸽子，然后和女神去约会，当然和女神约会玩，基友的局还没结束则会去继续和基友浪，如果没找到只能和女神说拜拜了。
三是自己会然醒悟，要去学习，把自己的计划安排全部清空，不论是女神还是基友，但是就是清空，有人来约他照样会去。

题解：

线段树每个节点维护九个值：
d, n, s ------- 分别表示屌丝， 女神， 学习的懒惰标记。
两棵树放在一起维护：
dls, drs, dms ----- 分别表示区间从左端开始最长的连续可用区间，区间从右端开始连续的最长可用的区间，以及区间的最长连续区间的长度。（表示屌丝）。
nls, nrs, nms ----- 相应的表示女神。
每次更新的时候如果是屌丝就去屌丝的树上找，如果是女神去屌丝树上先找，如果找不到就去女神树上继续找。

**代码： **

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn = 1e5 + 10;

struct node {
    int b, e, s, n, d;
    int nls, nrs, nms;
    int dls, drs, dms;
} t[maxn << 2];
void push_up(int node) {
    if (t[node << 1].nls == t[node << 1].e - t[node << 1].b + 1) {
        t[node].nls = t[node << 1].nls + t[(node << 1) | 1].nls;
    } else {
        t[node].nls = t[node << 1].nls;
    }

    if (t[(node << 1) | 1].nrs ==
        t[(node << 1) | 1].e - t[(node << 1) | 1].b + 1) {
        t[node].nrs = t[(node << 1) | 1].nrs + t[node << 1].nrs;
    } else {
        t[node].nrs = t[(node << 1) | 1].nrs;
    }
    t[node].nms = max(max(t[node << 1].nms, t[(node << 1) | 1].nms),
                      t[node << 1].nrs + t[(node << 1) | 1].nls);

    if (t[node << 1].dls == t[node << 1].e - t[node << 1].b + 1) {
        t[node].dls = t[node << 1].dls + t[(node << 1) | 1].dls;
    } else {
        t[node].dls = t[node << 1].dls;
    }

    if (t[(node << 1) | 1].drs ==
        t[(node << 1) | 1].e - t[(node << 1) | 1].b + 1) {
        t[node].drs = t[(node << 1) | 1].drs + t[node << 1].drs;
    } else {
        t[node].drs = t[(node << 1) | 1].drs;
    }
    t[node].dms = max(max(t[node << 1].dms, t[(node << 1) | 1].dms),
                      t[node << 1].drs + t[(node << 1) | 1].dls);
}

void push_down(int node) {
    if (t[node].s) {
        t[node << 1].dls = t[node << 1].drs = t[node << 1].dms =
            t[node << 1].e - t[node << 1].b + 1;
        t[node << 1].nls = t[node << 1].nrs = t[node << 1].nms =
            t[node << 1].e - t[node << 1].b + 1;
        t[(node << 1) | 1].dls = t[(node << 1) | 1].drs =
            t[(node << 1) | 1].dms =
                t[(node << 1) | 1].e - t[(node << 1) | 1].b + 1;
        t[(node << 1) | 1].nls = t[(node << 1) | 1].nrs =
            t[(node << 1) | 1].nms =
                t[(node << 1) | 1].e - t[(node << 1) | 1].b + 1;
        t[node << 1].s = t[(node << 1) | 1].s = 1;
        t[node << 1].n = t[(node << 1) | 1].n = 0;
        t[node << 1].d = t[(node << 1) | 1].d = 0;
        t[node].s = 0;
    }
    if (t[node].n) {
        t[node << 1].nls = t[node << 1].nrs = t[node << 1].nms = 0;
        t[node << 1].dls = t[node << 1].drs = t[node << 1].dms = 0;
        t[(node << 1) | 1].nls = t[(node << 1) | 1].nrs =
            t[(node << 1) | 1].nms = 0;
        t[(node << 1) | 1].dls = t[(node << 1) | 1].drs =
            t[(node << 1) | 1].dms = 0;

        t[node << 1].n = t[(node << 1) | 1].n = 1;
        t[node << 1].d = t[(node << 1) | 1].d = 0;
        t[node].n = 0;
    }

    if (t[node].d) {
        t[node << 1].dls = t[node << 1].drs = t[node << 1].dms = 0;
        t[(node << 1) | 1].dls = t[(node << 1) | 1].drs =
            t[(node << 1) | 1].dms = 0;

        t[node << 1].d = t[(node << 1) | 1].d = 1;
        t[node].d = 0;
    }
}
void create(int bb, int ee, int node) {
    t[node].b = bb, t[node].e = ee;
    t[node].s = t[node].n = t[node].d = 0;
    if (bb == ee) {
        t[node].nls = t[node].nrs = t[node].nms = 1;
        t[node].dls = t[node].drs = t[node].dms = 1;
        return;
    }
    int mid = (bb + ee) >> 1;
    create(bb, mid, node << 1);
    create(mid + 1, ee, (node << 1) | 1);
    push_up(node);
}

void update(int bb, int ee, int node, int opt) {
    if (bb <= t[node].b && ee >= t[node].e) {
        if (opt == 1) {
            t[node].dls = t[node].drs = t[node].dms = 0;
            t[node].d = 1;
        }
        if (opt == 2) {
            t[node].dls = t[node].drs = t[node].dms = 0;
            t[node].nls = t[node].nrs = t[node].nms = 0;
            t[node].n = 1;
            t[node].d = 0;
        }
        if (opt == 3) {
            t[node].dls = t[node].drs = t[node].dms = t[node].e - t[node].b + 1;
            t[node].nls = t[node].nrs = t[node].nms = t[node].e - t[node].b + 1;
            t[node].s = 1;
            t[node].d = t[node].n = 0;
        }
        return;
    }
    push_down(node);
    int mid = (t[node].b + t[node].e) >> 1;
    if (bb > mid)
        update(bb, ee, (node << 1) | 1, opt);
    else if (ee <= mid)
        update(bb, ee, node << 1, opt);
    else {
        update(bb, mid, node << 1, opt);
        update(mid + 1, ee, (node << 1) | 1, opt);
    }
    push_up(node);
}

int query(int node, int opt, int k) {
    if (t[node].b == t[node].e) {
        return t[node].b;
    }
    push_down(node);
    if (opt == 1) {
        if (t[node << 1].dms >= k) {
            return query(node << 1, opt, k);
        } else if (t[node << 1].drs + t[(node << 1) | 1].dls >= k) {
            return t[node << 1].e - t[node << 1].drs + 1;
        } else {
            return query((node << 1) | 1, opt, k);
        }
    }
    if (opt == 2) {
        if (t[node << 1].nms >= k) {
            return query(node << 1, opt, k);
        } else if (t[node << 1].nrs + t[(node << 1) | 1].nls >= k) {
            return t[node << 1].e - t[node << 1].nrs + 1;
        } else {
            return query((node << 1) | 1, opt, k);
        }
    }
    return -1;
}

int main() {
    int tt, n, m, cnt = 0;
    scanf("%d", &tt);
    while (tt--) {
        scanf("%d %d", &n, &m);
        create(1, n, 1);
        printf("Case %d:\n", ++cnt);
        for (int i = 0; i < m; i++) {
            int tmp, l, r;
            char ch[20];
            scanf("%s", ch);
            if (ch[0] == 'D') {
                scanf("%d", &tmp);
                int k;
                if (t[1].dms >= tmp)
                    k = query(1, 1, tmp);
                else
                    k = -1;
                if (k == -1) {
                    printf("fly with yourself\n");
                } else {
                    printf("%d,let's fly\n", k);
                    update(k, k + tmp - 1, 1, 1);
                }
            }
            if (ch[0] == 'N') {
                scanf("%d", &tmp);
                int k;
                if (t[1].dms >= tmp)
                    k = query(1, 1, tmp);
                else
                    k = -1;
                if (k == -1) {
                    int kk;
                    if (t[1].nms >= tmp)
                        kk = query(1, 2, tmp);
                    else
                        kk = -1;
                    if (kk == -1) {
                        printf("wait for me\n");
                    } else {
                        printf("%d,don't put my gezi\n", kk);
                        update(kk, kk + tmp - 1, 1, 2);
                    }
                } else {
                    printf("%d,don't put my gezi\n", k);
                    update(k, k + tmp - 1, 1, 2);
                }
            }
            if (ch[0] == 'S') {
                scanf("%d %d", &l, &r);
                update(l, r, 1, 3);
                printf("I am the hope of chinese chengxuyuan!!\n");
            }
        }
    }
    return 0;
}

3.2 特殊构造题

2014-2015 ACM-ICPC, Asia Tokyo Regional Contest G.Flipping Parentheses
题意： 给定一个由’(‘和’)‘组成的字符串s，每次给定一个t，将s[t]变化为另一个种类的括号(左括号变成右括号，右括号变成左括号)。要求在t前找到一个tmp位置，使得s[tmp]变化为另一个种类的括号后，整个s字符串仍然平衡。平衡意味着s中的左括号都能在后面找到一个右括号和他匹配。$字符串长度n<=3\ast 10^5,询问次数m<=1.5\ast 10^5$
题解： 对于这个括号序列，我们可以将’(‘设为1，’)‘设为-1，那么就能算出他们的前缀和,所有的前缀和都是大于等于0的。
如果我们改变一个’(‘并且他的位置是x，那么[x, n]范围内的前缀都-2。那么一旦找到其位置tmp以后，区间[tmp,n]上的前缀和都+2。所以只要在p之前找到一个’)‘将其转换就可以了。题目要求越靠左越好，那就从头开始找到第一个’)‘即可。注意到如果从头开始，还没出现’)‘之前，所有的’(‘的值都是和他本身相同的。
如果我们改变一个’)‘并且他的位置是x，那么[x, n]范围内的前缀都+2，我们同样的需要寻找一个’('将其转换。此时寻找其位置tmp的时候，要保证[tmp,n]后面所有的前缀和都要大于等于2。所以我们就寻找第一个满足条件的这个位置就好了。注意到只要右区间上最小的那个值都大于等于2，就可以往左区间去找。找到以后要加一。
代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 3e5 + 10;
int dat1[N << 2], lazy[N << 2], sum[N], n, m, dat2[N << 2]; // dat1=max, dat2 = min
char s[N];

void pushup(int rt) { 
    dat1[rt] = max(dat1[rt << 1], dat1[rt << 1 | 1]);
    dat2[rt] = min(dat2[rt << 1], dat2[rt << 1 | 1]);
    return;
}

void build(int rt, int l, int r) {
    if (l == r) {
        dat1[rt] = dat2[rt] = sum[l];
        lazy[rt] = 0;
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);
    return;
}

void pushdown(int rt, int l, int r) {
    if (lazy[rt]) {
        dat1[rt << 1] += lazy[rt], dat1[rt << 1 | 1] += lazy[rt], lazy[rt << 1] += lazy[rt];
        dat2[rt << 1] += lazy[rt], dat2[rt << 1 | 1] += lazy[rt], lazy[rt << 1 | 1] += lazy[rt];
        lazy[rt] = 0;
    }
    return;
}

void modify(int rt, int l, int r, int L, int R, int y) {
    if (L <= l && r <= R) {
        dat1[rt] += y;
        dat2[rt] += y;
        lazy[rt] += y;
        return;
    }
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) modify(rt << 1, l, mid, L, R, y);
    if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, y);
    pushup(rt);
    return;
}

int query1(int rt, int l, int r) {
    if (l == r) return l;
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (dat1[rt << 1] != mid) return query1(rt << 1, l, mid);   //如果从头开始，还没出现')'之前，所有的'('的值都是和他本身相同的。
    else return query1(rt << 1 | 1, mid + 1, r);
}

int query2(int rt, int l, int r) {
    if (l == r) return l;
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (dat2[rt << 1 | 1] >= 2) return query2(rt << 1, l, mid);   //只要右区间上最小的那个值都大于等于2，就可以往左区间去找。找到以后要加一。
    else return query2(rt << 1 | 1, mid + 1, r);
}

int main() {
    cin >> n >> m;
    scanf("%s", s + 1);
    int len = strlen(s + 1);
    for (int i = 1; i <= len; ++i) {
        if (s[i] == '(') sum[i] = sum[i - 1] + 1;
        else sum[i] = sum[i - 1] - 1;
    }
    build(1, 1, n);
    for (int i = 1, t; i <= m; ++i) {
        scanf("%d", &t);
        if (s[t] == '(') {
            modify(1, 1, n, t, n, -2);
            s[t] = ')';
            int tmp = query1(1, 1, n);
            s[tmp] = '(';
            modify(1, 1, n, tmp, n, 2);
            printf("%d\n", tmp);
        }
        else {
            modify(1, 1, n, t, n, 2);
            s[t] = '(';
            int tmp = query2(1, 1, n) + 1;
            s[tmp] = ')';
            modify(1, 1, n, tmp, n, -2);
            printf("%d\n", tmp);
        }
    }
    return 0;
}

Codeforces Round #684 (Div. 2) E.Greedy Shopping

题意： 有n个数字，这n个数字单调不增，有m个操作：

操作1： 1 x y, 把前1 ~ x个数字都与y取max

操作2：2 x y, 询问从第x个数字开始往后，最多有几个数字的和小于等于y

题解： 可以使用线段树维护区间和，区间长度，区间最小值和最大值。对于操作1，就是区间修改；对于操作2，如果当前的y小于区间最小值，那么直接return，如果当前y大于当前区间和，那么直接把区间和减掉y。

代码：

#include <bits/stdc++.h>

using namespace std;

int const N = 2e5 + 10, NN = N * 4;
typedef long long LL;
typedef pair<int, int> PII;

int n, m, T;
LL sum[NN];
int len[NN], minv[NN], maxv[NN], lazy[NN], a[N];

void pushup(int u) {
    sum[u] = sum[u << 1] + sum[u << 1 | 1];
    len[u] = len[u << 1] + len[u << 1 | 1];
    minv[u] = min(minv[u << 1], minv[u << 1 | 1]);
    maxv[u] = max(maxv[u << 1], maxv[u << 1 | 1]);
    return;
}

void build(int u, int l, int r) {
    if (l == r) {
        sum[u] = a[l], len[u] = 1, maxv[u] = minv[u] = a[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r) ;
    pushup(u);
}

void pushdown(int u, int l, int r) {
    int mid = (l + r) >> 1;
    if (!lazy[u]) return ;
    minv[u << 1] = minv[u << 1 | 1] = maxv[u << 1] = maxv[u << 1 | 1] = lazy[u];
    sum[u << 1] = (LL)len[u << 1] * lazy[u], sum[u << 1 | 1] = (LL)len[u << 1 | 1] * lazy[u];
    lazy[u << 1] = lazy[u << 1 | 1] = lazy[u], lazy[u] = 0;
    return;
}

void modify(int u, int l, int r, int L, int R, int y) {
    if (minv[u] >= y) return;
    if (l >= L && r <= R && maxv[u] < y) {
        sum[u] = (LL)y * len[u], minv[u] = maxv[u] = y, lazy[u] = y;
        return;
    }
    pushdown(u, l, r);
    int mid = (l + r) >> 1;
    if (L <= mid) modify(u << 1, l, mid, L, R, y);
    if (mid < R) modify(u << 1 | 1, mid + 1, r, L, R, y);
    pushup(u);
    return;
}

int query(int u, int l, int r, int L, int R, int &y) {
    if (minv[u] > y) return 0;
    if (l >= L && r <= R && sum[u] <= y) {
        y -= sum[u];
        return len[u];
    }
    pushdown(u, l, r);
    int mid = (l + r) >> 1;
    int res = 0;
    if (L <= mid) res += query(u << 1, l, mid, L, R, y);
    if (mid < R) res += query(u << 1 | 1, mid + 1, r, L, R, y);
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); 
    build(1, 1, n);
    for (int i = 1; i <= m; ++i) {
        int op, x, y;
        scanf("%d%d%d", &op, &x, &y);
        if (op == 1) modify(1, 1, n, 1, x, y);
        else printf("%d\n", query(1, 1, n, x, n, y));
    }
    return 0;
}