【零基础入门哈希签名架构，从Lamport到SPHINCS+】第五集 SPHINCS 2015 SPHINCS+ 2019（完结撒花）

严天龙

已于 2024-04-27 16:57:25 修改

阅读量3.5k

点赞数 14

文章标签：哈希算法架构算法 1024程序员节

于 2023-10-23 16:14:40 首次发布

本文链接：https://blog.csdn.net/m0_50572808/article/details/133958548

版权

第一集哈希签名始祖 Lamport 方案及其改进版本（Merkle，Winternitz）
第二集哈希签名树 Merkle Tree Authentication
第三集 HORS Hash to Obtain Random Subset 2002、DBS算法 2008
第四集 GMSS、XMSS、Multi Tree XMSS
第五集 SPHINCS 2015 SPHINCS+ 2019（完结撒花）

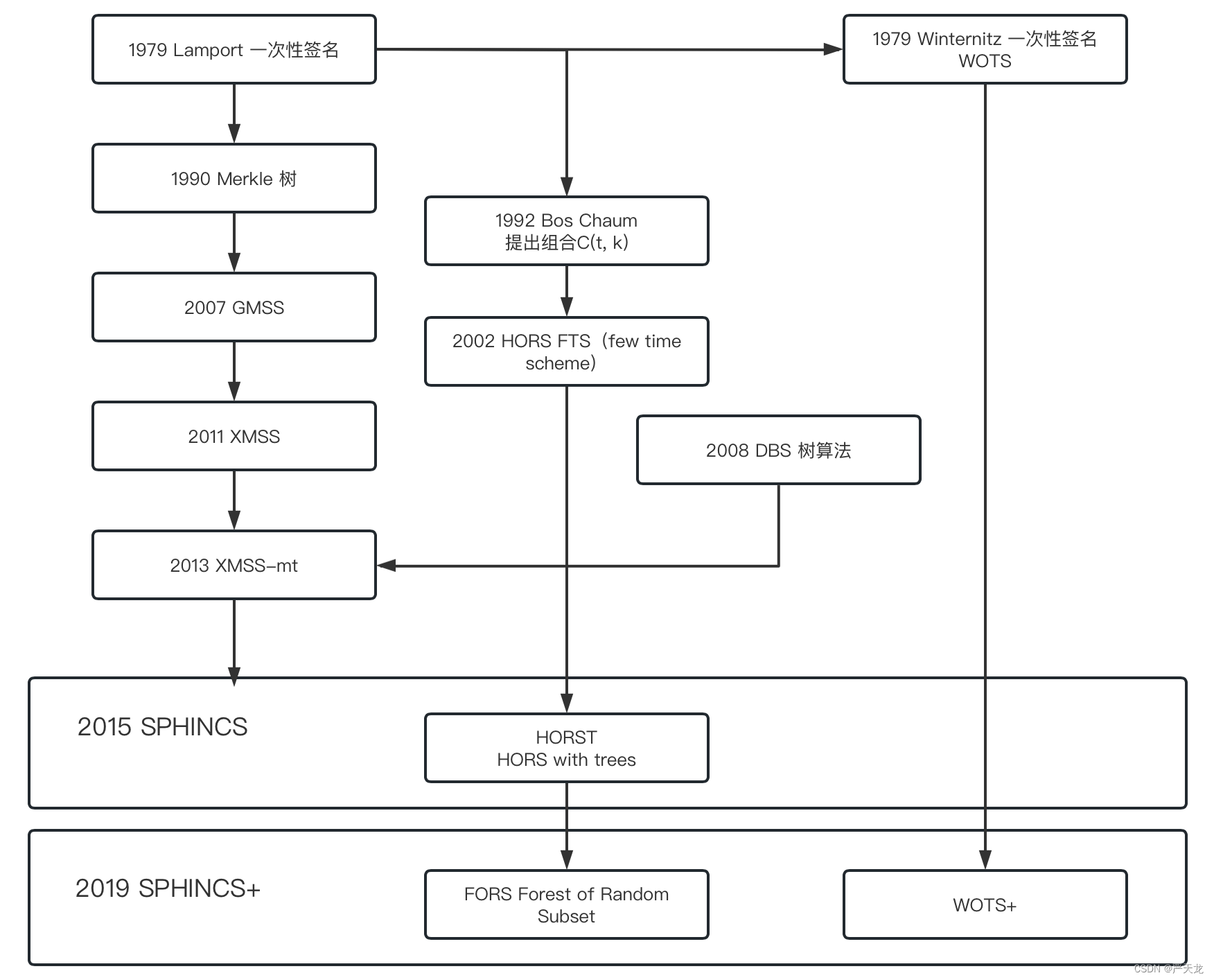
在这里插入图片描述

一、SPNICS 2015

Daniel J. Bernstein等人在2015年发布的论文《SPHINCS: practical stateless hash-based
signatures》

其总体框架和XMSS MT区别不大，都是“超树”结构。
在这里插入图片描述

SPHINCS 在XMSS MT的基础上创新性的点有两个：

提出了HORST（HORS Tree），在HORS的基础上，结合Merkle Tree的树结构思想，可以让公钥从 $t * l$ 减小到 $l$ （）。这在第三集的 三、HORS的问题和 SPHINCS中提出对应的解决方案 中提到过。因为HORS是一种FTS（Few Time Signature），所以也是在SPHINCS中，第一次提到把FTS结合到XMSS MT结构中。大大增加了密钥对的可重用性。
使用了“密钥种子”代替密钥，减小了密钥对的大小。

1.1 HORST

在这里插入图片描述
从结构图我们可以看到，SPHINCS的总体架构和XMSS MT是一样的。不同点在于最后一层树 $TREE_0$ 的叶子节点，SPHINCS连接的的是HORST的签名，而XMSS MT连接的是WOTS的签名。如下图所示：

一个是OTS（WOTS），一个FTS（HORST），因此与XMSS MT对比，SPHINCS能够签名的数量大大增加。

1.2 密钥种子

由于SPHINCS中有大量的WOTS和HORST，每一个WOTS和HORST就会有大量的密钥对（即私钥和公钥），如果直接把这些密钥对放在一起当作是整个SPHINCS算法（超树）的的密钥对，会显得很庞杂。所以为了方便以及减小密钥对的大小，SPHINCS提出了“用密钥生成密钥”的思想。

SPHINCS的密钥对组成如下：
私钥：SK，公钥：PK
$SK = (SK_1,SK_2,Q)$
$PK=(PK_1,Q)$

1.2.1 私钥

先说一下私钥 $SK = (SK_1,SK_2,Q)$
$SK_1$ 和 $SK_2$ ，是通过采样得到（随机采样），长度均为 $n$
$(SK_1,SK_2) \in \{0,1\}^n \times \{0,1\}^n$

$Q$ 是随机掩码，我们之前提到过，比如说在两个字节点结合成一个父节点的时候，会加一个随机掩码。SPHINCS中的随机掩码有很多中，除了有这个作用以外（应用在超树中），还应用于WOTS，HORST中。 $Q$ 也是采样得到的，在不同的应用中， $Q$ 的长度也不同。这里放一个原论文的图：
在这里插入图片描述

1.2.1.1 SK1的作用

生成地址 $(d-1||0||i),\ i \in [2^{h/d}-1]$ ， $A$ 指的是节点在子树中的地址（位置）。
首先，计算 $2^{h/d}-1$ 的值，得到一个整数。然后，将 $i$ 从 1 递增到 $2^{h/d}-1$ ，每次取一个整数值，并将其转换为二进制表示形式。
例如，假设 $h = 6$ ， $d = 2$ ，那么 $2^{h/d}-1 = 7$ 。（高为3层的树，一共有1+2+4=7个节点）在此示例中，我们需要计算 $A$ 的所有可能取值，即 $A$ 应包含从 1 到 7 的所有整数值，并将它们转换为二进制表示形式。
最终，我们可以得到 $A$ 的计算结果如下：
$A = \{(0||0||1),\ (0||1||0),\ (0||1||1),\ (1||0||0),\ (1||0||1),\\\ (1||1||0),\ (1||1||1)\}$
其中， $∣∣$ 是分隔符号，并且使用了二进制表示形式来表示 $i$ 的值。请注意， $i$ 的取值范围是 $2^{h/d}-1]$ ，即由 $1$ 到 $2^{h/d}-1$ 的整数值。
生成种子 $\mathcal S_A \leftarrow \mathcal F_a(A,SK_1)$
$\mathcal F$ 是PRF（Pseudorandom Random Function 伪随机函数）
生成WOTS+的公钥 $\mathrm {pk}_A \leftarrow \mathrm{WOTS.kg}(\mathcal S_A,Q_{\mathrm {WOTS+}})$

1.2.1.2 SK2的作用

与message $M$ 进过一个函数 $\mathcal F$ 得到一个数 $R$ ，长度为 $2 n$ ，前n bit为 $R_1$ ，后n bit为 $R_2$
$\leftarrow \mathcal F(M,SK_2),\ \ R=(R_1,R_2) \in \{0,1\}^n \times \{0,1\}^n$
$R_1$ 与message $M$ 进过一个函数 $\mathcal H$ 得到摘要Digest $D$
$\leftarrow \mathcal H(R_1,M)$
$R_2$ 用于确定用哪一棵HORTS树，在超树的最底层（超树的叶子节点），就是一颗颗的HORS Trees（HORSTs），取 $R_2$ 的前 $h$ bit作为HORST的 index索引 $i$ （从左到右数，所以刚好是 $2^h$ 颗HORSTs，h是超树的层数）
$\leftarrow \mathrm{CHOP}(R_2,h)$

1.2.2 公钥

这里说的公钥是整一个SPHINCS的公钥 $PK_1$ ，也就是整个超树的根节点。

1.3 总结

SPHINCS的其余细节我就不再多说了，因为在SPHINCS+中，会对其做出一些改变，大家只需要理解其整体框架即可。

二、SPHINCS+

SPHINCS+也是Daniel J. Bernstein发布的，是在SPHINCS的基础上完善而成的。

Daniel J. Bernstein在2019年发布的论文《The SPHINCS+ Signature Framework》

SPHINCS+与SPHINCS的不同之处就是，SPHINCS+将HORST换成了FORS（Forest of Random Subsets），在总体框架上，没有其他的改变，还是使用超树结构。当然，在上有一些改动，使得整个算法更加完善。
SPHINCS和SPHINCS+对比图
SPHINCS+总体框架图

2.1 FORS

2.1.1 复习一下HORST

回顾一下之前的HORST，就是在HORS的基础上，将许多公钥用树结构串起来。
首先是HORS，这里放一段第三集中的原文：

我们先确定参数，这里用 $l = 80, k = 20, t = 256$ 。 $k$ 和 $t$ 我们之前已经解释过了，就是全集有 $t$ 个元素，从中取出 $k$ 个元素作为子集。这里的 $l$ 是每个元素的长度，即每个元素长 $l$
bit

先确定message，原文没有强调message的长度，只要求message $m$ 在经过哈希函数 $H a s h (m) = h$ 之后的输出 $h$ 的长度不超过 $k*log_2t=20*log_2256=20*8=160$
bits。如果长度不足，可以在后面补0

随机生成密钥对（私钥和公钥）：在确定了参数之后，我们马上就可以生产私钥和公钥了。私钥就是随机生成整一个全集，包含了 $256$ 个元素，每个元素长 $80$
bit 。即有私钥： $s_1,s_2,\dots,s_{256})$ 。然后让私钥经过一个“One Way Function”
$f$ ，就是一个单向函数，得到公钥 $PK=(k,v_1,v_2,\dots,v_{256})$ 。这里产生公钥的方法和之前我们提到的所有的哈希签名方案是一样的。

签名信息：让message $m$ 经过哈希函数 $H a s h (m) = h$ 之后的得到 $h$ 。将h分成20块 $h_1,h_2,\dots,h_{20}$ ，每一块为8
bits，可以表示0到255之间的数。比如 $h_1=148,h_2=33,\dots,h_{20}=106$
这里的十进制数，刚好对应上了私钥 $S K$ 中的1到256个 $s$ 元素，我们选出私钥中对应的元素作为签名。签名为：
$\sigma=(s_{148},s_{33},\dots,s_{106})$
这就是从256个元素中选出20个元素当作子集，同时由于可能存在message长度不足的情况， $h$ 会在后面补0以满足160
bit，因此后面的 $h$ 就表示为0，没有对应的私钥 $s_0$ ，导致可能最终只是选出了十几个元素。这时候就利用上了“最多为k（20）个元素的子集”这个改进点了。(仔细观察你会发现，虽然没有 $s_0$ ，但是有 $s_{256}$ ，所以0对应的私钥可以是 $s_{256}$ ，加上这个私钥可以看作是在签名的后面补0的操作)

验证：Receiver收到 $\sigma=(s_1',\dots ,s_k'),PK=(k,v_1,v_2,\dots,v_{256})$ 。让message
$m$ 经过哈希函数 $H a s h (m) = h$ 之后的得到 $h$ 。将h分成20块 $h_1,h_2,\dots,h_{20}$ ，每一块为8
bits，可以表示0到255之间的数。比如 $h_1=148,h_2=33,\dots,h_{20}=106$ 将签名经过函数 $f$ ，
第一个元素得到 $f(s_1')$ ，将 $f(s_1')$ 与公钥 $P K$ 中对应位置的元素 $v_{148}$ 进行对比，如果相等 $f(s_1')= v_{148}$ 。签名的第一个元素 $s_1'$ 验证为“真”。将签名经过函数 $f$ ，
第二个元素得到 $f(s_2')$ ，将 $f(s_2')$ 与公钥 $P K$ 中对应位置的元素 $v_{33}$ 进行对比，如果相等 $f(s_2')= v_{33}$ 。签名的第二个元素 $s_2'$ 验证为“真”。后面的20个元素用同样的方法验证即可。

2.1.2 FORS的改变

在HORST中，不同块 $h_i$ 之间的私钥和公钥是共用的，都是从一个公共的密钥池 $S K$ 中取密钥。而在FORS中，不同块 $h_i$ 都有自己私自的密钥池 $SK_i$

举个例子，参数 $k=6,a=3,t=8=2^a$ ，即从8个元素中取出6个元素作为子集。

按照HORST的方法，随机生成私钥 $s_1,s_2,\dots,s_{8})$ ，让message $m$ 经过哈希函数 $H a s h (m) = h$ 之后的得到 $h$ 。将h分成6块： $h_1=4,h_2=2,\dots,h_{6}=7$ ，最后得到签名 $\sigma=(s_{4},s_2,\dots,s_{7})$
FORS：因为要选6个元素作为子集，于是随机生成6个私钥池 $SK_i=(k, s_1^i,s_2^i,\dots,s_{8}^i),\ i \in[0,5]$ ，让message $m$ 经过哈希函数 $H a s h (m) = h$ 之后的得到 $h$ 。将h分成6块： $h_1=4,h_2=2,\dots,h_{6}=7$ ，最后得到签名 $\sigma=(s_{4}^0,s_2^1,\dots,s_{7}^5)$ 。如下图所示：

FORS的优点：

对比HORST，FORS能够更充分地利用密钥对，也就是同一个密钥对，能够签名更多的消息。

密钥对大小增大了 $k$ 倍，能够签名的数量从 $\frac{2^t}{\sqrt{k\pi}}$ 增加到了 $2^t*k$ ，也就是增加了 $\sqrt k\pi *k$ 倍，所以变向减小了密钥对的大小。在同等的签名次数下，FORS使用的密钥对更小了。

三、总结

SPHINCS+的总体框架我们已经讲完了，就是在SPHINCS的基础上，将HORST变成FORS。

到目前为止，你已经完全了解SPHINCS+基本原理是怎么运作的了。

最后再放一下SPHINCS+的总体框架图
SPHINCS+总体框架图

四、One More Thing

之后我还会写几篇文章，来讲一下SPHINCS+的各种细节，包括官方提交到GitHub上的源代码怎么在Windows和Mac上跑通（目前我已经在这两个平台上跑通了），以及我们一直提到的哈希函数到底具体是怎么运算的，等等关于SPHINCS+的一切。

如何跑通 SPHINCS+官方代码（Mac和Windows两平台）