前言
属性图聚类是一个具有挑战性的问题,它要求图结构和节点的联合建模属性。虽然图卷积已经被证明在整合结构和特征信息时是非常有效的,但是几乎没有研究说明如何应用它来最大化集群性能。现有的方法基本上都是使用图卷积的固定的(忽略了图的多样性)低阶的(只考虑每个节点几跳内的邻居,没有充分利用节点关系)顺序。在本文中,我们提出了一种自适应的利用高阶图卷积实现属性图聚类的图卷积方法来捕获全局簇结构,并自适应地为不同的图选择合适的顺序。我们对基准测试进行分析和大量实验数据集从理论上验证了我们方法的有效性。实证结果表明我们的方法是可行的,比最先进的方法要好。
属性图聚类
- 目标:在属性图中聚类节点(属性图中的每一个节点都关联着一组特征属性)
- 主要思路:相邻的节点往往处于同一集群,如果同一集群中的节点具有相似的特征表示,则集群化将变得更加容易。我们没有像GCN那样堆叠很多层,我们设计了一个k阶图卷积,作为节点特征的低通图滤波器来获得平滑的特征表示,其中k可以通过簇内距离自适应地选择
方法介绍
谱域的图卷积:

- p( Λ \Lambda Λ)是一个频响函数,可对 Λ \Lambda Λ中的值(特征值)进行放缩
- f 和
f
‾
\overline{f}
f 分别是经过图滤波器G卷积前后的图信号

这里 f 可以看做一组基信号(拉普拉斯矩阵 L s L_s Ls分解得到)的加权
拉普拉斯矩阵 L s L_s Ls= U U U Λ \Lambda Λ U − 1 U^{-1} U−1 -
U
U
U=[
u
1
u_1
u1,…,
u
n
u_n
un]代表n个基向量,
Λ
\Lambda
Λ=diag(
λ
1
\lambda_1
λ1,…,
λ
n
\lambda_n
λn),
λ
q
\lambda_q
λq的大小可以反映
u
q
u_q
uq的平滑程度
即

图上的平滑程度反映了相邻节点的相似程度 - 高频:不平滑,特征值大
- 低频:平滑,特征值小
由此我们知道,在一组基中,相对平滑的图信号更有利于聚类,那么便自然地想到,我们应当筛选低频信号,抑制高频信号,也就是要压缩较大的特征值,那么如何实现呢?
回到上面提到的频响函数 p(
Λ
\Lambda
Λ),可以通过它设计恰当的p来实现我们的目的:
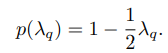

由此可得,一阶图卷积为
X
‾
\overline{X}
X=(
I
I
I-1/2
L
s
L_s
Ls)X
推出 k阶图卷积为 X ‾ \overline{X} X=( I I I-1/2 L s L_s Ls) k ^k kX
最后一个问题,图卷积的k阶该如何确定?
作者使用了一个启发式的方法,逐渐增加k,当类内距离开始变小时,停止搜索(类内距离越小,类间距离越大,聚类效果好)
总结
本文提出了一种简单有效的属性图聚类方法:为了更好地利用可用数据和捕获全局簇结构,我们设计了k阶图卷积来聚合更远的数据信息。为了优化在不同图上的聚类性能,我们设计了一种策略,自适应地选择一个合适的k。这使得我们的方法与经典的和最先进的方法相比,具有竞争性的性能。在未来的工作中,我们计划改进自适应选择策略,使我们的方法更加鲁棒和高效。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








