人工智能及其应用复习大纲

1、问题求解过程的两种主要形式表示方法，它们各自有些什么搜索算法？

• 状态空间表示法
  • A搜索算法、A*搜索算法、回溯法
• 与/或树表示法–(问题规约法)
  • 极大极小法、α-β剪枝法、AO*搜索算法、AO算法、与或树的有序搜索

2、知识的表示方法及特点

• 一阶谓词逻辑
  • 优点：自然性、精确性、严密性、容易实现
  • 缺点：不能表示不确定的知识、组合爆炸、效率低
• 产生式
  • 优点：自然性、模块性、有效性、清晰性
  • 缺点：效率不高、不能表达结构性知识
• 框架
  • 结构性、继承性、自然性
• 语言网络
  • 优点：结构性、自然性
  • 缺点：非严格性、处理上的复杂性
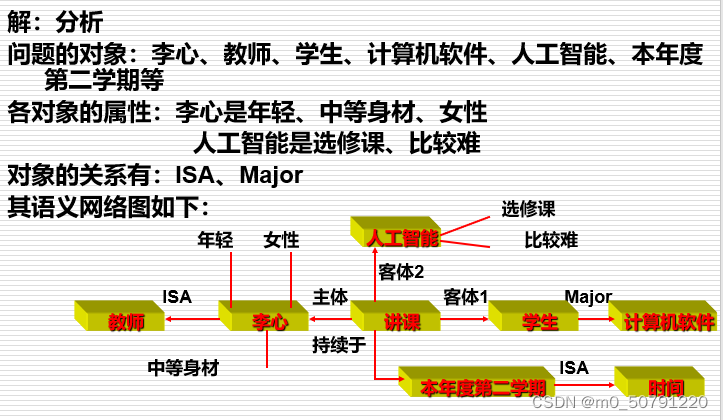
  • 对象关系：ISA、AKO、AMO、part_of

自然数是大于零的整数
所有整数不是偶数就是奇数
偶数除以2是整数

定义谓词
$N(x)表示x是自然数I(x)表示x是整数$
$E(x)表示x是偶数O(x)表示x是奇数$
$GZ(x)表示x大于0$
一阶谓词逻辑
$(\forall x)(N(x)\to GZ(x)\wedge I(x))$
$(\forall x)(I(x)\to E(x)\vee O(x))$
$(\forall x)(E(x)\to I(f(x)))其中，函数f(x)=x/2$

李心是一位年轻的女教师，中等身材，她在本年度第二学期给计算机软件专业的学生讲授“人工智能”课程，该课程是一门选修课，比较难。

3、将谓词公式化成子句集

$$P\to Q\iff \neg P\vee Q$$

$$P\leftrightarrow Q\iff (P\wedge Q)\vee (\neg P\wedge Q)$$

$(\forall x)((\forall y)P(x,y)\to \neg (\forall y)(Q(x,y)\to R(x,y)))$

$(\forall x)(\neg (\forall y)P(x,y)\vee \neg (\forall y)(\neg Q(x,y)\vee R(x,y))$
$(\forall x)((\exists y)\neg P(x,y)\vee (\exists y)(Q(x,y)\wedge \neg R(x,y)))$
$(\forall x)((\exists y)\neg P(x,y)\vee (\exists z)(Q(x,z)\wedge \neg R(x,z)))$
$(\forall x)(\neg P(x,f(x))\vee (Q(x,g(x))\wedge \neg R(x,g(x))))$
$(\forall x)((\neg P(x,f(x))\vee Q(x,g(x)))\wedge (\neg P(x,f(x))\vee \neg R(x,g(x))))$
$(\neg P(x,f(x))\vee Q(x,g(x))\wedge (\neg P(x,f(x))\vee \neg R(x,g(x)))$
子句集： { ¬ P ( x , f ( x ) ) ∨ Q ( x , g ( x ) ) , ¬ P ( x , f ( x ) ) ∨ ¬ R ( x , g ( x ) ) } \{ \lnot P(x,f(x))\lor Q(x,g(x)),\lnot P(x,f(x))\lor \lnot R(x,g(x))\} {¬P(x,f(x))∨Q(x,g(x)),¬P(x,f(x))∨¬R(x,g(x))}

在子句集中各子句是合取关系

4、给出子句集，写出其归结过程

$C_1=P(a)\vee \neg Q(x)\vee R(x),C_2=\neg P(y)\vee Q(b)$

二元归结式不唯一

令 L 1 = P ( a ) , L 2 = ¬ P ( y ) ，则 σ = { a / y } 是 L 1 与 L 2 的最一般合一 L_1=P(a),L_2=\lnot P(y)，则\sigma=\{ a/y\}是L_1与L_2的最一般合一 L1​=P(a),L2​=¬P(y)，则σ={a/y}是L1​与L2​的最一般合一
$C_1\sigma =P(a)\vee \neg Q(x)\vee R(x),C_2\sigma =\neg P(a)\vee Q(b)$
C 12 = ( C 1 σ − { L 1 σ } ) ∨ ( C 2 σ − { L 2 σ } ) C_{12}=(C_1\sigma -\{L_1\sigma\})\lor(C_2\sigma-\{L_2\sigma\}) C12​=(C1​σ−{L1​σ})∨(C2​σ−{L2​σ})
C 12 = ( { P ( a ) , ¬ Q ( x ) , R ( x ) } − { P ( a ) } ) ∨ ( { ¬ P ( a ) , Q ( b ) } − { ¬ P ( a ) } ) C_{12}=(\{P(a),\lnot Q(x),R(x)\}-\{P(a)\})\lor(\{\lnot P(a),Q(b)\}-\{\lnot P(a)\}) C12​=({P(a),¬Q(x),R(x)}−{P(a)})∨({¬P(a),Q(b)}−{¬P(a)})
C 12 = ( { ¬ Q ( x ) , R ( x ) } ) ∨ ( { Q ( b ) } ) C_{12}=(\{\lnot Q(x),R(x)\})\lor(\{Q(b)\}) C12​=({¬Q(x),R(x)})∨({Q(b)})
C 12 = { ¬ Q ( x ) , R ( x ) , Q ( b ) } C_{12}=\{\lnot Q(x),R(x),Q(b)\} C12​={¬Q(x),R(x),Q(b)}
$C_{12}=\neg Q(x)\vee R(x)\vee Q(b)$

5、已知个体域D，求公式F在D上的解释，并指出在每一种解释下公式F的真值

D = { 1 , 2 } , F = ( ∃ x ) ( ∀ y ) ( P ( x , y ) → Q ( x , y ) ) D=\{1,2\},F=(∃x)(∀y)(P(x,y)\rightarrow Q(x,y)) D={1,2},F=(∃x)(∀y)(P(x,y)→Q(x,y))

6、判断子句集是否是不可满足的

子句集S归结出NIL：不可满足的
不存在任何方法归结出空子句，S是可满足的

7、Skolem标准形的一般形式为：$(\forall x_1)(\forall x_2)\dots (\forall x_n)M$，其中$M$是子句的合取，将公式化为Skolem标准形

$$P\vee (Q\wedge R)\iff (P\vee Q)\wedge (P\vee R)$$

$$(P\wedge Q)\vee (P\wedge R)\iff P\wedge (Q\vee R)$$

8、应用归结反演证明方法求解问题

$F_1:\text{王先生(Wang)是小李(Li)的老师}$
$F_2:\text{小李与小张(Zhang)是同学}$
$F_3:\text{如果x与y是同班同学，则x的老师也是y的老师}$
$Q:\text{求小张的老师是谁？}$

0. 定义谓词
   $T(x,y)\text{：x是y的老师}$
   $C(x,y)\text{：x是y的同学}$
1. 把已知前提及待求解的问题表示成谓词公式
   $F_1:T(Wang,Li)$
   $F_2:C(Li,Zhang)$
   $F_3:(\forall x)(\forall y)(\forall z)(C(x,y)\wedge T(x,z)\to T(z,y))$
   $Q:\neg (\exists x)T(x,Zhang)\vee ANSWER(x)$
2. 将谓词公式转子句集
   （1）$T(Wang,Li)$
   （2）$C(Li,Zhang)$
   （3）$\neg C(x,y)\vee \neg T(z,x)\vee T(z,y)$
   （4）$\neg T(u,Zhang)\vee ANSWER(u)$
3. 应用归结原理
   （5）$\neg C(Li,y)\vee T(Wang,y)$ （1）与（3）归结
   （6） $\neg C(Li,Wang)\vee ANSWER(Wang)$ （4）与（5）归结
   （7）$ANSWER(Wang)$ （2）与（6）归结

9、用归结反演进行问题的证明

Q 为 { P i } 的逻辑结论 ( P 1 ∧ P 2 ∧ ⋅ ⋅ ⋅ ∧ P n ) ∧ ¬ Q 不可满足 Q为\{P_i\}的逻辑结论\quad(P_1\land P_2 \land···\land P_n)\land \lnot Q\quad不可满足 Q为{Pi​}的逻辑结论(P1​∧P2​∧⋅⋅⋅∧Pn​)∧¬Q不可满足

规则1：任何人的兄弟不是女性
规则2：任何人的姐妹必是女性
事实：Mary是Bill的姐妹
求证：Mary不是Tome的兄弟

1.定义谓词
$brother(x,y)\text{x是y的兄弟}$
$sister(x,y)\text{x是y的姐妹}$
$woman(x)\text{x是女性}$
$\text{规则1:}\forall x\forall y(brother(x,y)\to \neg woman(x))$
$\text{规则2:}\forall x\forall y(sister(x,y)\to woman(x))$
$\text{事实 :}sister(Maruy,Bill)$
$\text{求证 :}\neg brother(Mary,Tom)$
2.子句集
$C_1=\neg brother(x,y)\vee \neg woman(x)$
$C_2=\neg sister(x,y)\vee woman(x)$
$C_3=sister(Maruy,Bill)$
$C_{23}=woman(Mary)$
$C_{123}=\neg brother(Mary,y)$
$C_4=brother(Mary,Tom)注意这里是\neg Q$
$C_{1234}=NIL$

10、对博弈树进行α-β剪枝搜索

或节点：选择最大子节点得分值
与节点：选择最小子节点得分值

1. 任何“或”节点x的a值如果不能降低其父节点的b值，则对节点x以下的分枝可停止搜索，并使x的倒推值为a。这种剪枝称为b剪枝。
2. 任何“与”节点x的b值如果不能升高其父节点的a值，则对节点x以下的分枝可停止搜索，并使x的倒推值为b。这种剪枝称为a剪枝。
3. 最优a-b剪枝法：在a-b剪枝技术中，一个节点的第一个子节点的倒推值（或估值）是很重要的。对于一个“或”节点，如果估值最高的子节点最先生成，或者对于一个“与”节点，估值最低的子节点最先生成，则被剪除的节点数最多，搜索的效率最高。

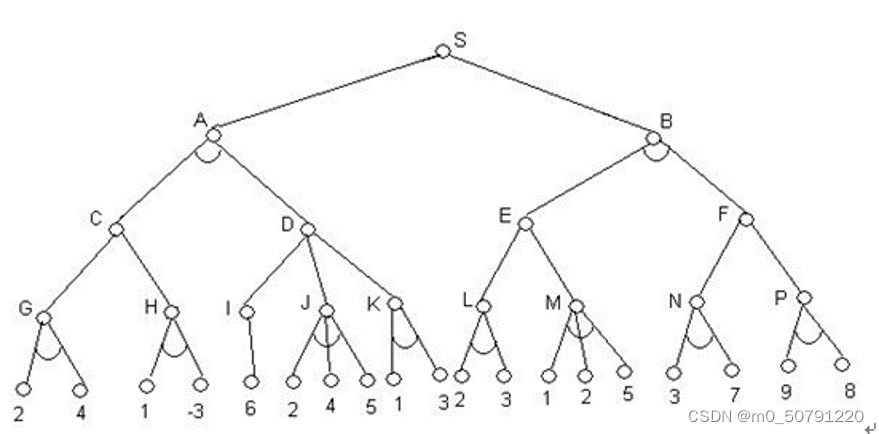
倒推值
$h(G)=2,h(H)=-3,h(I)=6,h(J)=2,h(K)=1,h(L)=2,h(M)=1,h(N)=3,h(P)=8$
$h(C)=2,h(D)=6,h(E)=2,h(F)=8$
$h(A)=2,h(B)=2$
$h(S)=2$
$\alpha$剪枝：
$\beta$剪枝：

11、证明子句集S是不可满足的

12、对与/或树，分别按照和代价法与最大代价法求解树及其解树的代价

终止节点：$h(x)=0$
非终止节点且不可扩展：$h(x)=\infty$
或节点：$\swarrow -\searrow$

• h ( x ) = m i n { c ( x , y i ) + h ( y i ) } h(x)=min\{c(x,y_i)+h(y_i)\} h(x)=min{c(x,yi​)+h(yi​)}

与节点：$\swarrow \searrow$

• 和代价法：$h(x)=\sum (c(x,y_i)+h(y_i))$
• 最大代价法： h ( x ) = m a x { c ( x , y i ) + h ( y i ) } h(x)=max\{c(x,y_i)+h(y_i)\} h(x)=max{c(x,yi​)+h(yi​)}
  

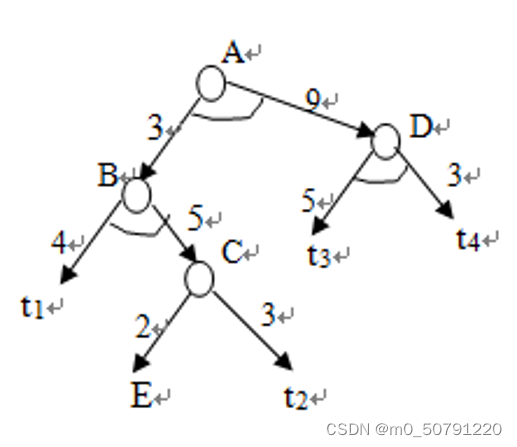
解树
$A,B,t_1,C,t_{2}A,D,t_3.t_4$

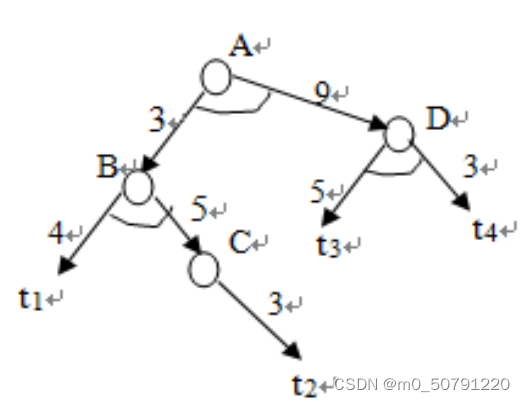
和代价法
$h(C)=3,h(B)=12,h(D)=8,h(A)=32$
最大代价法
$h(C)=3,h(B)=8,h(D)=5,h(A)=14$

13、遗传算法的基本步骤和主要特点？

特点：

• 可以直接对结构对象进行操作
• 利用随机技术来指导对一个被编码的参数空间进行高效搜索
• 采用群体搜索策略,易于并行化
• 仅用适应度函数值来评估个体，并在此基础上进行遗传操作，使种群中个体之间进行信息交换。

14、群智能算法的基本思想是什么？

模拟自然界的生物个体之间的协同行为，通过个体之间的合作和竞争来实现全局优化。
SI：受群体智能启发的算法
群体智能：由简单个体组成的群落与环境以及个体之间的互动行为

15、简述粒子群算法的流程

16、蚁群算法的搜索原理及蚁群算法的特点

• 搜索原理：
  • 蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。其选择一条路径的概率与该路径上分泌物的强度成正比。因此，由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象：某一条路径走过的蚂蚁越多，后面的蚂蚁选择该路径的可能性就越大。蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。
  • 通过个体之间的信息交流与相互协作最终找到从蚁穴到食物源的最短路径
  • 信息素跟踪：按照一定的概率沿着信息素较强的路径觅食
  • 信息素遗留：会在走过的路上会释放信息素，使得在一定的范围内的其他蚂蚁能够觉察到并由此影响它们的行为
• 特点
  • 分布式合作：蚁群算法是并行的，每只蚂蚁独立工作，可以在分布式计算环境中高效执行
  • 正反馈机制：一条路径走过的蚂蚁越多，后面的蚂蚁选择该路径的可能性就越大
  • 鲁棒性和自适应性：算法能够适应环境变化，如路径阻塞或出现新路径，通过信息素更新机制重新寻找最优路径
  • 并行化能力：蚁群算法是并行的，每只蚂蚁独立工作，可以在分布式计算环境中高效执行

17、列举几种典型的群智能算法，分析它们的主要优点、缺点

• 粒子群优化算法PSO
  • 优点
    • 简单易实现：算法结构简单，参数较少，易于理解和实现
    • 快速收敛：对于一些问题，PSO能够较快收敛到较优解
    • 并行处理：每个粒子独立运行，支持并行运算
    • 全局搜索能力：适当调整参数，PSO能在搜索空间较好平衡全局与局部的搜索
  • 缺点
    • 易陷入局部最优：没有有效的机制防止早熟收敛，可能导致错过全局最优解
    • 参数敏感：算法性能高度依赖参数设置，例如惯性权重、加速常数
    • 缺乏智能决策：粒子的移动基于简单规则，缺乏复杂的决策逻辑
• 量子粒子群优化算法
  • 优点：相对于粒子群优化算法具有更好的收敛性和全局搜索能力
  • 缺点：求解约束优化问题的时候
    1.会产生大量的不可行解
    2.破坏种群的多样性
    3.导致算法陷入局部极值
• 人工蜂群算法ABC
  • 优点
    • 具有全局寻优能力：ABC算法通过信息共享和局部搜索等策略，可以有效地避免陷入局部最优解，从而具有全局寻优能力。
    • 参数设置简单：ABC算法只需要设置蜜蜂数量和终止条件等少量参数，使得算法使用更加简单。
    • 适用范围广：ABC算法不依赖于被优化问题的具体形式，可以应用于不同类型的优化问题。
    • 鲁棒性强：ABC算法能够处理具有噪声和非线性特性的优化问题，具有较强的鲁棒性
  • 缺点
    • 收敛速度慢：ABC算法需要进行大量的随机搜索和信息交流，收敛速度相对较慢。
    • 精度较低：由于ABC算法采用了随机搜索的策略，因此可能会出现局部最优解较多的情况，导致精度较低。
    • 对参数敏感：虽然ABC算法参数较少，但是这些参数对算法的性能影响较大，需要根据不同的问题进行调整
• 蚁群算法 ACO
  • 优点
    • 蚁群算法的参数较少，设置简单，因而该算法易于应用到组合优化问题的求解
    • 蚁群算法是一种自组织的算法
    • 蚁群算法具有较强的鲁棒性，蚁群算法具有较强的鲁棒性
    • 蚁群算法是一种本质上的并行算法。每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信
  • 缺点
    • 收敛速度慢。蚁群算法中信息素初值相同，选择下一个节点时倾向于随机选择。