任务安排1
题目描述

数据范围
1
≤
N
≤
5000
,
0
≤
S
≤
50
,
1
≤
T
i
,
C
i
≤
100
1≤N≤5000,0≤S≤50,1≤Ti,Ci≤100
1≤N≤5000,0≤S≤50,1≤Ti,Ci≤100
令
s
u
m
c
[
i
]
sumc[i]
sumc[i]:花费的前缀和
s u n t [ i ] sunt[i] sunt[i]:时间的前缀和
如果选择在第 i i i个任务处添加一个分组,那么在这里多出来的机器启动时间 S S S会对后面的每一个任务都造成影响,导致多出来的花费值是 S ∗ ( s u m c [ n ] − s u m c [ i ] ) S*(sumc[n] - sumc[i]) S∗(sumc[n]−sumc[i]),为了不影响后面的dp,所以对后面的任务造成的花费直接在 i i i处加上。
定义f[i]表示前i个任务分组的最小花费。
则有 f i = m i n { f j + s u m t i ∗ ( s u m c i − s u m c j ) + S ∗ ( s u m c n − s u m c j ) ∣ 0 ≤ j ≤ i − 1 } f_i=min \{ f_j + sumt_i*(sumc_i-sumc_j) + S*(sumc_n-sumc_j) \ \ | \ 0 \le j \le i-1 \ \} fi=min{fj+sumti∗(sumci−sumcj)+S∗(sumcn−sumcj) ∣ 0≤j≤i−1 }
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n, s;
long long dp[N], sumt[N], sumc[N];
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> s;
for (int i = 1; i <= n; i ++) {
cin >> sumt[i] >> sumc[i];
sumt[i] += sumt[i - 1];
sumc[i] += sumc[i - 1];
}
memset(dp, 0x3f, sizeof dp);
dp[0] = 0;
for (int i = 1; i <= n; i ++) {
for (int j = 0; j < i; j ++) {
dp[i] = min(dp[i], dp[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));
}
}
cout << dp[n];
return 0;
}
任务安排2
题意与任务安排1相同,但是数据范围有变。
数据范围:
1
≤
N
≤
3
×
1
e
5
,
1
≤
T
i
,
C
i
≤
512
,
0
≤
S
≤
512
1≤N≤3×1e5,1≤Ti,Ci≤512,0≤S≤512
1≤N≤3×1e5,1≤Ti,Ci≤512,0≤S≤512
之前的做法是 O ( n 2 ) O(n^2) O(n2),但是本题 n ≤ 3 e 5 n\le3e5 n≤3e5,于是需要对上面的转移式子进行优化。
这里要用到的就是斜率优化dp。
在求 f i f_i fi时,需要遍历每一个 f j , ( j < i ) f_j,(j\lt i) fj,(j<i),我们可以把与i相关的值看成常量,将与j有关的值看成变量。
更具体的,将 f j f_j fj看成 y y y, s u m c j sumc_j sumcj看成 x x x。
for (int i = 1; i <= n; i ++) {
for (int j = 0; j < i; j ++) {
f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));
}
}
f i = f j − ( s u m t i + S ) ∗ s u m c j + s u m t i ∗ s u m c i + S ∗ s u m c n f_i=f_j - (sumt_i + S) * sumc_j + sumt_i * sumc_i + S * sumc_n fi=fj−(sumti+S)∗sumcj+sumti∗sumci+S∗sumcn
左右移项得到 f j = ( s u m t i + S ) ∗ s u m c j + f i − s u m t i ∗ s u m c i − S ∗ s u m c n f_j = (sumt_i+S) *sumc_j + f_i - sumt_i * sumc_i - S * sumc_n fj=(sumti+S)∗sumcj+fi−sumti∗sumci−S∗sumcn
可以将其看成直线表达式: y = k x + b y = kx + b y=kx+b的形式。其中斜率 k k k是一个定值。
这个直线表达式上的点 ( x , y ) (x, y) (x,y)取值可以是: ( s u m c 0 , f 0 ) , ( s u m c 1 , f 1 ) , ( s u m c 2 , f 2 ) , . . . , ( s u m c i − 1 , f i − 1 ) (sumc_0, f_0), (sumc_1,f_1), (sumc_2,f_2), ..., (sumc_{i-1}, f_{i-1}) (sumc0,f0),(sumc1,f1),(sumc2,f2),...,(sumci−1,fi−1)。不同的取值代入上面的式子可以得到不同的 f i f_i fi。我们的目标是使得 f i f_i fi最小,也就是让直线表达式中的截距 b b b最小。
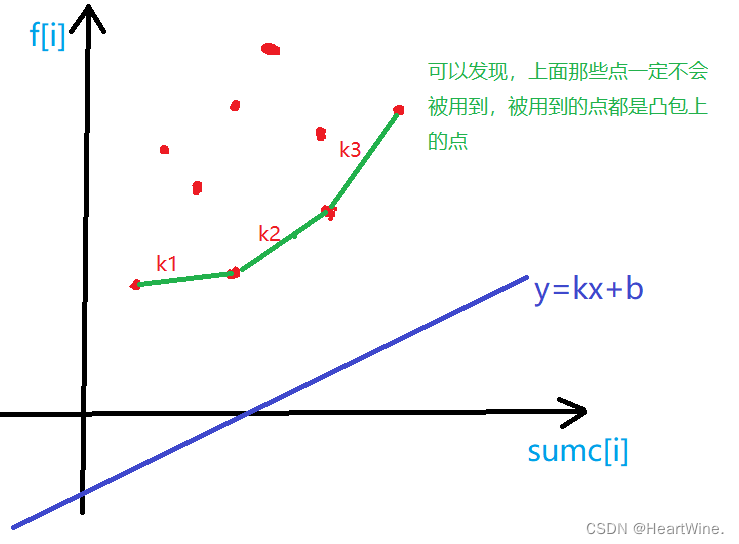
根据上图,我们需要维护这些点的凸包的下边界,因为对于某一个直线来说,与它距离最近的点一定是在这些点上。
- 如果该直线的斜率为k,怎么找到与它距离最近的点?
我们将凸包上的相邻两点组成直线的斜率标出来,如上图,可以发现 k 1 < k 2 < k 3 k_1<k_2<k_3 k1<k2<k3。
而 k 1 < k < k 2 k_1<k<k_2 k1<k<k2。于是我们只需要找到第一个斜率大于k的位置的点。
- 另外,本题还有一些其他性质,由于这两个特殊的性质,我们可以进行均摊 O ( 1 ) O(1) O(1)的转移。
1、斜率 k = s u m t i + S k=sumt_i+S k=sumti+S,因为 t t t和 S S S都是大于 0 0 0的,所以我们从 1 1 1到 n n n求 f i f_i fi时,其对应询问的直线的斜率是单调递增的。
因此,在查询时,如果队头某些点(斜率小于当前直线斜率)不可能作为答案,那么它在后面时更不可能作为答案,可以直接删除。
2、我们不断新加点 ( s u m c j , f j ) (sumc_j,f_j) (sumcj,fj)时,新加点的横坐标也是单调递增的。因为 c c c是大于 0 0 0的。
这意味着我们新加入的点一定不会被删掉。如果新加的点可以和队列末尾的点组成凸包,那么加进去,否则将末尾的点删掉,直到可以和队列中的点组成凸包。
#include <bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define all(x) begin(x),end(x)
#define debug(x) cout<<#x<<": "<<x<<endl;
using namespace std;
using ll = long long;
const int N = 3e5 + 10;
int n, s, q[N];
ll c[N], t[N], f[N];
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> s;
for (int i = 1; i <= n; i ++) {
cin >> t[i] >> c[i];
t[i] += t[i - 1];
c[i] += c[i - 1];
}
int hh = 0, tt = -1;
q[++ tt] = 0; // (c[0], f[0])
for (int i = 1; i <= n; i ++) {
// 求f[i], 对应直线斜率k=t[i]+s
// hh < tt 确保队列中有>=2个点,若队头点组成的斜率小于当前斜率,出队
while (hh < tt && (f[q[hh + 1]] - f[q[hh]]) <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) hh ++;
int j = q[hh]; // 此时最优转移点就是队头的点
f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];
//将点(c[i], f[i])加入队列,加入前将不符合条件的点出队
while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt --;
q[++ tt] = i;
}
cout << f[n] << endl;
return 0;
}
CF1715E Long Way Home
题意

数据范围:
1
≤
n
,
m
≤
1
e
5
,
1
≤
k
≤
20
,
1
≤
w
≤
1
e
9
1 \le n,m \le1e5,1 \le k \le 20,1 \le w \le 1e9
1≤n,m≤1e5,1≤k≤20,1≤w≤1e9。
我们先用 d i j s t r a dijstra dijstra求出 d i s t i dist_i disti,表示只走道路从 1 1 1到 i i i的最小值。
- 然后考虑只飞一次,能使得 d i s t i dist_i disti如何更新?
另设一个数组 d p dp dp,其中 d p i dp_i dpi表示飞完后从 1 1 1到 i i i的最短花费。
对于
d
i
s
t
i
dist_i
disti,我们只需要处理从
1
1
1到
i
i
i最后一次是飞的最短花费。
即其路线是
1
→
j
→
i
1 \to j \to i
1→j→i,那么
d
p
i
=
m
i
n
{
d
i
s
t
j
+
(
i
−
j
)
2
∣
1
≤
j
≤
n
}
dp_i=min\{dist_j + (i-j)^2 \ \ | 1\le j \le n \ \}
dpi=min{distj+(i−j)2 ∣1≤j≤n }。
然后更新之后我们将所有被更新过的点放入优先队列中在跑一边
d
i
j
s
t
r
a
dijstra
dijstra。
这样就得到了只飞一次的最小花费。
题目要求
k
k
k次,且
k
≤
20
k\le20
k≤20,那么我们循环
k
k
k次这个过程即可。
- 还有一个问题是转移方程是 O ( n ) O(n) O(n)的一个转移,求 n n n个合起来就是 O ( n 2 ) O(n^2) O(n2),显然需要优化。
d
p
i
=
m
i
n
{
d
i
s
t
j
+
(
i
−
j
)
2
∣
1
≤
j
≤
n
}
dp_i=min\{dist_j + (i-j)^2 \ \ | 1\le j \le n \ \}
dpi=min{distj+(i−j)2 ∣1≤j≤n }。
可以写成
d
i
s
t
j
+
j
2
=
2
i
j
+
d
p
i
−
i
2
dist_j+j^2=2ij+dp_i-i^2
distj+j2=2ij+dpi−i2。
这里将其看成
y
=
k
x
+
b
y=kx+b
y=kx+b。
其中
Y
i
=
d
i
s
t
i
+
i
2
,
X
i
=
i
Y_i=dist_i+i^2,X_i=i
Yi=disti+i2,Xi=i。
注意本题也有与任务安排类似的特殊性质:即每个直线的斜率k是单调递增的,新加入的点的横坐标也是单调递增的。
有些题目不满足上面的性质,那么维护时就要使用一些其他的方法。
#include <bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define all(x) begin(x),end(x)
#define debug(x) cout<<#x<<": "<<x<<endl;
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
int n, m, k, q[N];
ll dist[N], dp[N];
vector<pair<int, int>> g[N];
bool vis[N];
priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<>> Q;
void dijkstra() {
memset(vis, 0, sizeof vis);
while (Q.size()) {
auto [d, u] = Q.top();
Q.pop();
if (vis[u]) continue;
vis[u] = true;
for (auto &[v, w]: g[u]) {
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
if (!vis[v]) Q.emplace(dist[v], v);
}
}
}
}
inline ll X(ll i) { return i; }
inline ll Y(ll i) { return dp[i] + i * i; }
inline double slope(ll i, ll j) { // 由于范围太大,交叉相乘判大小会溢出,只能用除法
return (double)(Y(j) - Y(i)) / (X(j) - X(i));
}
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m >> k;
while (m --) {
int u, v, w;
cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
Q.emplace(dist[1], 1);
dijkstra();
for (int _ = 1; _ <= k; _ ++) {
for (int i = 1; i <= n; i ++) dp[i] = dist[i];
// 维护所有点的凸包
int hh = 0, tt = -1;
for (int i = 1; i <= n; i ++) {
while (hh < tt && slope(q[tt - 1], q[tt]) >= slope(q[tt], i)) tt --;
q[++ tt] = i;
}
// 寻找最优转移点更新dist
for (int i = 1; i <= n; i ++) {
while (hh < tt && slope(q[hh], q[hh + 1]) <= 2ll * i) hh ++;
int j = q[hh];
if (dist[i] > dp[j] + (ll)(i - j) * (i - j)) {
dist[i] = dp[j] + (ll)(i - j) * (i - j);
Q.emplace(dist[i], i);
}
}
dijkstra();
}
for (int i = 1; i <= n; i ++) cout << dist[i] << " \n"[i == n];
return 0;
}
任务安排3
这一题与任务安排2唯一不同的还是数据范围。

可以发现,T存在负数。这样以来我们每次求
f
i
f_i
fi时,随着
i
i
i的递增,它们对应直线的斜率
t
i
+
S
t_i+S
ti+S不再是递增的了,这样我们就不能删除队头的点,因为以后的斜率可能会更小,有可能会用到队头的点,于是我们寻找最优转移点的时候只能在维护出来的凸包上二分。
复杂度变为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)。
(需要注意的是,本题数据在计算过程中会出现
l
o
n
g
l
o
n
g
long long
longlong溢出的情况,于是这里使用了
_
_
i
n
t
128
\_\_int128
__int128)
#include <bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define all(x) begin(x),end(x)
#define debug(x) cout<<#x<<": "<<x<<endl;
using namespace std;
using ll = long long;
template <typename T>
inline void read(T &x) {
x = 0; int f = 1;
char ch = getchar();
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
x *= f;
}
template <typename T, typename ...Args>
inline void read(T &t, Args &...args) {
read(t); read(args...);
}
template <typename T>
inline void write(T x) {
if (x < 0) x = -x, putchar('-');
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
inline void write(T x, char ch) {
write(x), putchar(ch);
}
const int N = 3e5 + 10;
int n, s, q[N];
__int128 t[N], c[N], f[N];
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
read(n, s);
for (int i = 1; i <= n; i ++) {
read(t[i], c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
int hh = 0, tt = -1;
q[++ tt] = 0;
for (int i = 1; i <= n; i ++) {
//二分
int l = hh - 1, r = tt;
while (l + 1 < r) {
int mid = l + r >> 1;
if ((f[q[mid + 1]] - f[q[mid]]) <= (t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) l = mid;
else r = mid;
}
int j = q[r];
f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];
while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt --;
q[++ tt] = i;
}
write(f[n], '\n');
return 0;
}
运输小猫
题意:
有
n
n
n座山,
m
m
m只喵,
P
P
P个饲养员。(编号从
1
1
1开始)
第
i
i
i座山与第
i
−
1
i-1
i−1座山之间相隔
d
i
d_i
di。
第
i
i
i只喵会在第
H
i
H_i
Hi座山上玩耍,直到时间
T
i
T_i
Ti才结束玩耍并等待饲养员来接她。
所有的饲养员一开始都在第
1
1
1座山。现在安排饲养员的出发时刻(可以是负数,理解为提前出发)。
每个饲养员的速度为
1
1
1米
/
/
/单位时间,他们会从
1
1
1号山走到
N
N
N号山接走在等待的喵。
你的任务是规划每个饲养员从
1
1
1 号山出发的时间,使得所有猫等待时间的总和尽量小。
数据范围
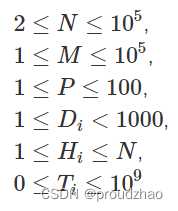
做法:
首先求一下山之间距离的前缀和,使得
d
i
d_i
di表示
1
1
1号山到
i
i
i号山的距离。
对于第
i
i
i只喵,设饲养员的出发时间为
S
S
S,则如果该饲养员能接到第
i
i
i只喵,意味着
S
+
d
H
i
≥
T
i
S+d_{H_i} \ge T_i
S+dHi≥Ti。所以第
i
i
i只喵要想能被接到,必须存在一个饲养员的出发时间
S
≥
T
i
−
d
H
i
S \ge T_i-d_{H_i}
S≥Ti−dHi。
对于所有的喵,我们可以求出来一个最早出发时间的数组
a
a
a,其中
a
i
=
T
i
−
d
H
i
a_i=T_i-d_{H_i}
ai=Ti−dHi。
对数组 a a a从小到大排序。对于一个饲养员,他一定是接走 a a a数组中连续的一批小喵。设饲养员接走的是区间 [ l , r ] [l,r] [l,r]内的小喵,那么该饲养员的出发时间为 a r a_r ar时对于当前区间是最优的。该批小喵的等待时间之和就是 a r − a l + a r − a l − 1 + . . . + a r − a r = ( r − l + 1 ) ∗ a r − ∑ i = l r a i a_r-a_l+a_r-a_{l-1}+...+a_r-a_r=(r-l+1)*a_r-\sum_{i=l}^ra_i ar−al+ar−al−1+...+ar−ar=(r−l+1)∗ar−∑i=lrai。
问题就转化成了,将 a a a数组分成最多 P P P段,每一段的代价是 ( r − l + 1 ) ∗ a r − ∑ i = l r a i (r-l+1)*a_r-\sum_{i=l}^ra_i (r−l+1)∗ar−∑i=lrai,使得总代价最小。然后我们就可以进行 d p dp dp了。(喜)
另
s
s
s数组为
a
a
a数组的前缀和。
状态表示为
f
j
,
i
f_{j,i}
fj,i:前
i
i
i只喵分成
j
j
j组的最小花费。
状态转移方程是
f
j
,
i
=
m
i
n
{
f
j
−
1
,
k
+
a
i
×
(
i
−
k
)
−
(
s
i
−
s
k
)
∣
0
≤
k
<
i
}
f_{j,i}=min\{ f_{j-1,k}+a_i \times (i-k)-(s_i-s_k) \ \ | 0 \le k \lt i\ \ \}
fj,i=min{fj−1,k+ai×(i−k)−(si−sk) ∣0≤k<i }。
显然直接
d
p
dp
dp是会超时的。
接下来就是斜率优化的过程。
f
j
,
i
=
f
j
−
1
,
k
+
a
i
×
(
i
−
k
)
−
(
s
i
−
s
k
)
f_{j,i}=f_{j-1,k}+a_i \times (i-k)-(s_i-s_k)
fj,i=fj−1,k+ai×(i−k)−(si−sk)。
左右移项得到
f
j
−
1
,
k
+
s
k
=
a
i
×
k
+
f
j
,
i
−
a
i
×
i
+
s
i
f_{j-1,k}+s_k=a_i \times k+f_{j,i}-a_i\times i+s_i
fj−1,k+sk=ai×k+fj,i−ai×i+si
将其看成直线
y
=
k
x
+
b
y=kx+b
y=kx+b。
有
Y
k
=
f
j
−
1
,
k
+
s
k
,
X
k
=
k
Y_k=f_{j-1,k}+s_k,X_k=k
Yk=fj−1,k+sk,Xk=k。
需要注意的是,我们在计算第
j
j
j层的值时,维护的是第
j
−
1
j-1
j−1层的凸包。
#include <bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define all(x) begin(x),end(x)
#define debug(x) cout<<#x<<": "<<x<<endl;
using namespace std;
using ll = long long;
const int N = 1e5 + 10, M = 110;
int n, m, p, q[N];
ll d[N], a[N], s[N], f[M][N];
ll Y(int j, int k) {
return f[j - 1][k] + s[k];
}
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n >> m >> p;
for (int i = 2; i <= n; i ++) {
cin >> d[i];
d[i] += d[i - 1];
}
for (int i = 1; i <= m; i ++) {
int h, t;
cin >> h >> t;
a[i] = t - d[h];
}
sort(a + 1, a + 1 + m);
for (int i = 1; i <= m; i ++) s[i] = s[i - 1] + a[i];
memset(f, 0x3f, sizeof f);
for (int i = 0; i <= p; i ++) f[i][0] = 0;
for (int j = 1; j <= p; j ++) {
int hh = 0, tt = -1;
q[++ tt] = 0;
for (int i = 1; i <= m; i ++) {
while (hh < tt && (Y(j, q[hh + 1]) - Y(j, q[hh]))
<= a[i] * (q[hh + 1] - q[hh])) hh ++;
int k = q[hh];
f[j][i] = f[j - 1][k] + a[i] * (i - k) - (s[i] - s[k]);
while (hh < tt && (Y(j, q[tt]) - Y(j, q[tt - 1])) * (i - q[tt])
>= (Y(j, i) - Y(j, q[tt])) * (q[tt] - q[tt - 1])) tt --;
q[++ tt] = i;
}
}
cout << f[p][m];
return 0;
}























 8717
8717











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








