如何理解高斯过程（三）：协方差矩阵

如何理解协方差矩阵和核函数的关系？

补充基础概念：

• 协方差：协方差衡量两个变量之间的线性关系方向与强度 

• 协方差矩阵：对角线是方差，非对角线是协方差

• 例子：来自deepseek

两个随机变量，

步骤1：均值 ,

步骤2：去中心化,

步骤3：计算协方差

步骤4：构建协方差矩阵

为什么方差和协方差一样呢？

答：去中心化之后，两个随机变量一样

和高斯核函数的关系：

协方差矩阵：

假设有一组变量 x=[1 4 8] 和 y=[1 4 8] 协方差矩阵 按照上述步骤，计算协方差矩阵为

高斯过程中的协方差矩阵：

通常我们需要计算Kff，这 是训练集输入的协方差矩阵kernel(trained_X,trained_X)

公式为：

注意：每个数值代表一个样本点，都需要计算，不是矩阵或者向量计算。

我们现在知道trained_X=[1 4 8]

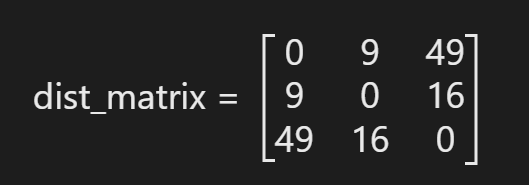，点与点距离的平方

再带入高斯核公式得到：

意义：值越相近，表现在协方差矩阵上就是接近1。

思考：

协方差矩阵和高斯过程中的协方差矩阵计算方式存在差别。两者在结构上具有相似之处。

但作用层次不同：协方差矩阵是将一个向量看成整体，而高斯过程是一个点一个点的去计算。

协方差矩阵非对角元素：衡量随机变量之间的相近程度

高斯过程的协方差矩阵：衡量样本点之间的相近程度