一. 斐波那契数列模型
解题步骤:
- 确定状态表示(最重要):明确 dp 表里的值所表示的含义
- 推导状态转移方程(最难):dp[i] 等于什么?
- 初始化:保证填表的时候不越界
- 填表顺序:明确执行动态规划时的填表顺序
- 返回结果:明确最终要返回的是那个子问题的值
1. 第 N 个泰波那契数

题目解析
我们对题目给的公式进行转化:
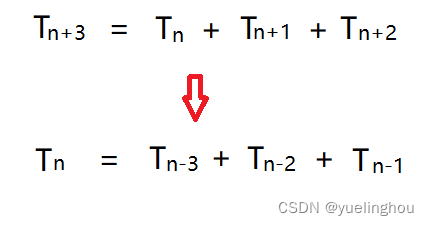
观察公式可以看到,如果要求第 i 个泰波那切数的话,我们只需知道前 i-1、i-2、i-3 的值即可。
算法原理
- 状态表示:dp[i] 代表第 i 个泰波那切数
- 状态转移方程:
dp[i] = dp[i-1] + dp[i-2] + dp[i-3] - 初始化:dp[0] = 0、dp[1] = dp[2] = 1
- 填表:根据状态转移方程和初始化的值,使用滑动窗口的方式一直计算最终得到第 i 个泰波那切数。
- 返回值:第 n 个泰波那切数
编写代码
class Solution
{
public:
int tribonacci(int n)
{
// 1、建表
vector<int> dp(n+1);
// 2、初始化
dp[0] = 0, dp[1] = dp[2] = 1;
// 3、填表
for(int i = 3; i <= n; ++i)
{
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
}
// 4、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
2. 三步问题
题目解析:小孩最多一次跳三步,假设要跳到第n级台阶,那最后跳到第n级台阶时的那一步一定是下面三种情况之一:
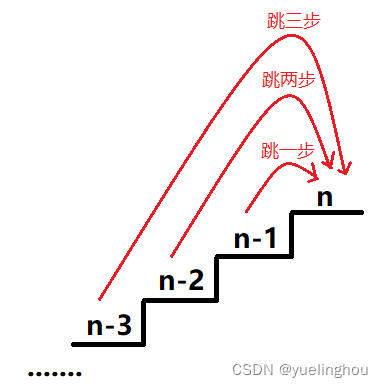
所以想求跳到第n级台阶有几种方法的话,我们只需知道跳到第 n-1、n-2 和 n-3 台阶时各自有几种方法,然后把它们相加起来即可。
PS:计算时需要注意取模
算法原理
- 状态表示:dp[i] 表示 到达i位置时,一共有多少种方法。
- 状态转移方程:dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
- 初始化:dp[1] = 1 dp[2] = 2 dp[3] = 4
- 填表顺序:从左往右
- 返回值 :dp[n]
代码实现
class Solution
{
public:
int waysToStep(int n)
{
// 1、处理特殊情况
if (n == 1) return 1;
if (n == 2) return 2;
if (n == 3) return 4;
// 2、创建dp表
vector<int> dp(n + 1);
// 3、初始化
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
// 4、填表
for (size_t i = 4; i <= n; ++i)
dp[i] = ((dp[i - 1] + dp[i - 2]) % 1000000007 + dp[i - 3]) % 1000000007;
// 5、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
3. 使用最小花费爬楼梯

题目解析
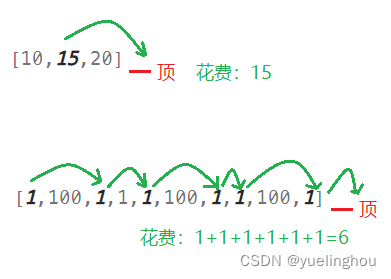
解法一:从左往右填表
- 状态表示:dp[i] 表示到达i位置时的最小花费
- 状态转移方程

- 初始化(保证填表的时候不越界):dp[0]=dp[1]=0
- 填表顺序:从左往右
- 返回值:因为是从0号台阶开始,所以最后一个台阶的下标为 n-1。最后返回 dp[n]
代码实现
class Solution
{
public:
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
// 1、建表 && 初始化
vector<int> dp(n + 1);
// 2、填表
for(int i = 2; i <= n; ++i)
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
// 3、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
解法二:从右往左填表
-
状态表示:dp[i] 表示从i位置出发,到达楼顶,此时的最小花费
-
状态转移方程

-
初始化:dp[n-1] = cost[n-1]、dp[n-2] = cost[n-2]
-
填表顺序:从右往左
-
返回值:min(dp[0], dp[1])
代码实现
class Solution
{
public:
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
vector<int> dp(n);
dp[n - 1] = cost[n - 1];
dp[n - 2] = cost[n - 2];
for (int i = n - 3; i >= 0; --i)
dp[i] = cost[i] + min(dp[i + 1], dp[i + 2]);
return min(dp[0], dp[1]);
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
4. 解码方法

题目解析
输入是一个只含有数字的非空字符串,要求返回所有可能存在的解码方式(注意单独一个0,和0x为非法数字,不能用来解码)
算法原理
状态表示:dp[i] 代表 以 i 位置为结尾时,解码方法的总数
状态转移方程:根据最近的一步,划分问题

初始化:情况转移方程情况复杂的话,我们可以考虑dp表多开一个空间这样方便我们后继填表,这时要注意多开出来的那块空间初,他始化的值要能够让我们的填表逻辑正确。
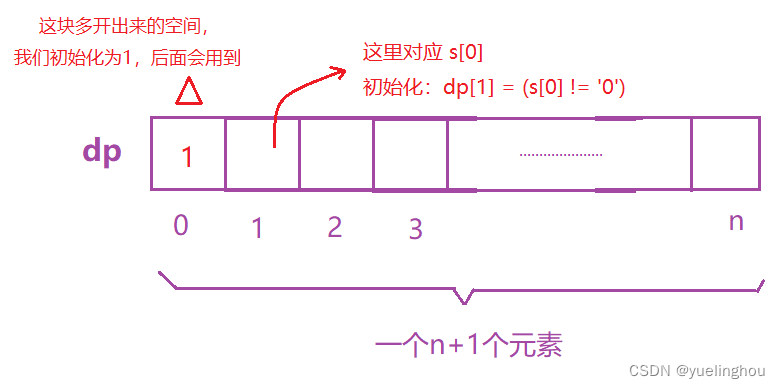
填表顺序:从左往右
返回值:dp[n]
代码实现
class Solution
{
public:
int numDecodings(string s)
{
// 1、建表
size_t n = s.size();
vector<int> dp(n + 1);
// 2、初始化
dp[0] = 1;
dp[1] = s[0] != '0';
// 3、填表
for (size_t i = 2; i <= n; ++i)
{
if (s[i - 1] != '0') dp[i] += dp[i - 1];
if (atoi(s.substr(i - 2, 2).c_str()) >= 10 && atoi(s.substr(i - 2, 2).c_str()) <= 26) dp[i] += dp[i - 2];
}
// 4、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
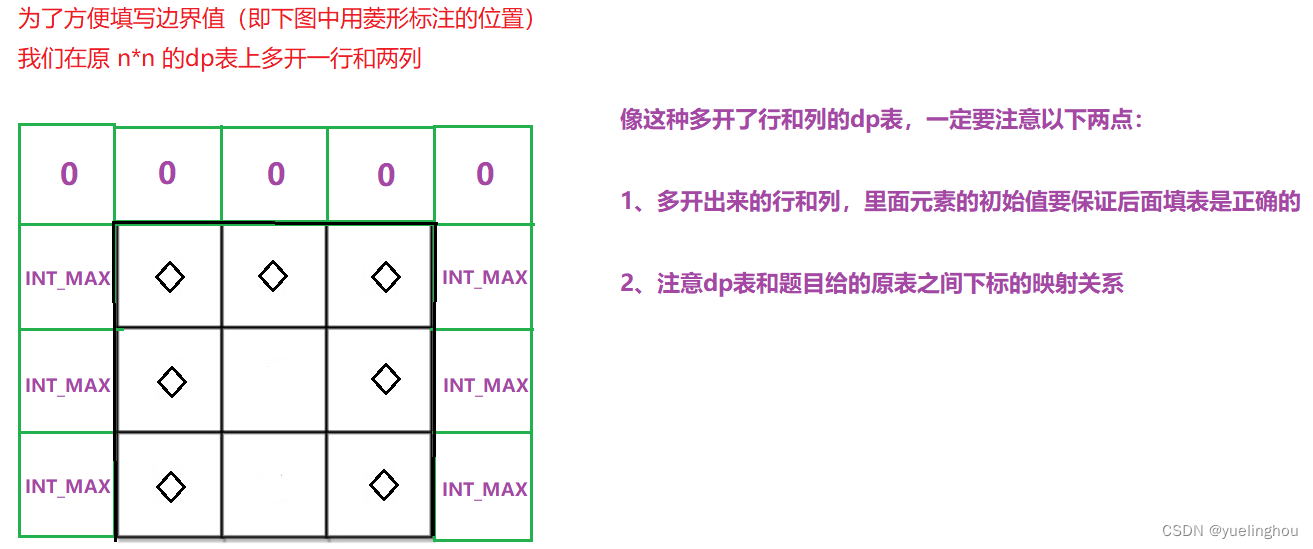
二. 路径问题
1. 不同路径

算法原理
-
状态表示:dp[ i ][ j ]的含义是:走到 (i, j) 位置,一共有多少种走法
-
状态转移方程:根据最近的一步去划分问题

-
初始化:为了方便填表,我们给dp表多开了一行和一列
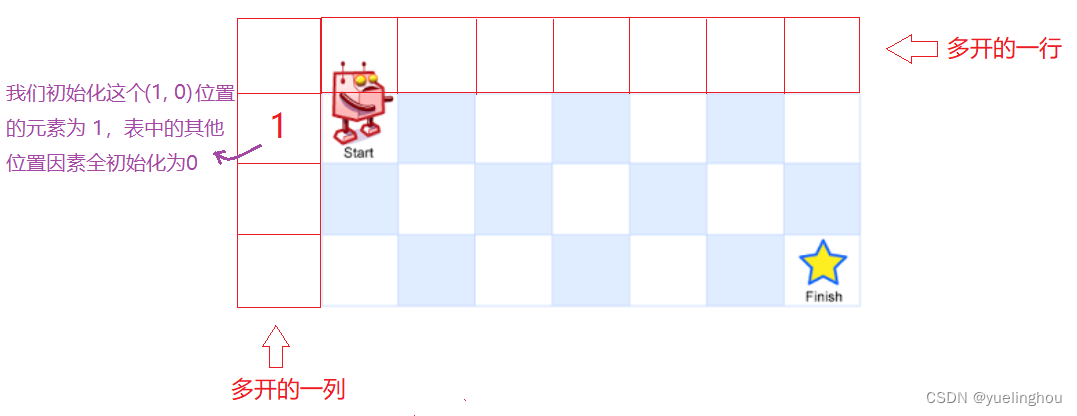
-
填表顺序:从上往下填写每一行,每一行再从左往右填写
-
返回值:dp[m][n]
代码实现
class Solution
{
public:
int uniquePaths(int m, int n)
{
// 1、建表
// 2、初始化
// 3、填表
// 4、返回值
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[1][0] = 1;
for (size_t i = 1; i <= m; ++i)
for (size_t j = 1; j <= n; ++j)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
2. 不同路径 II
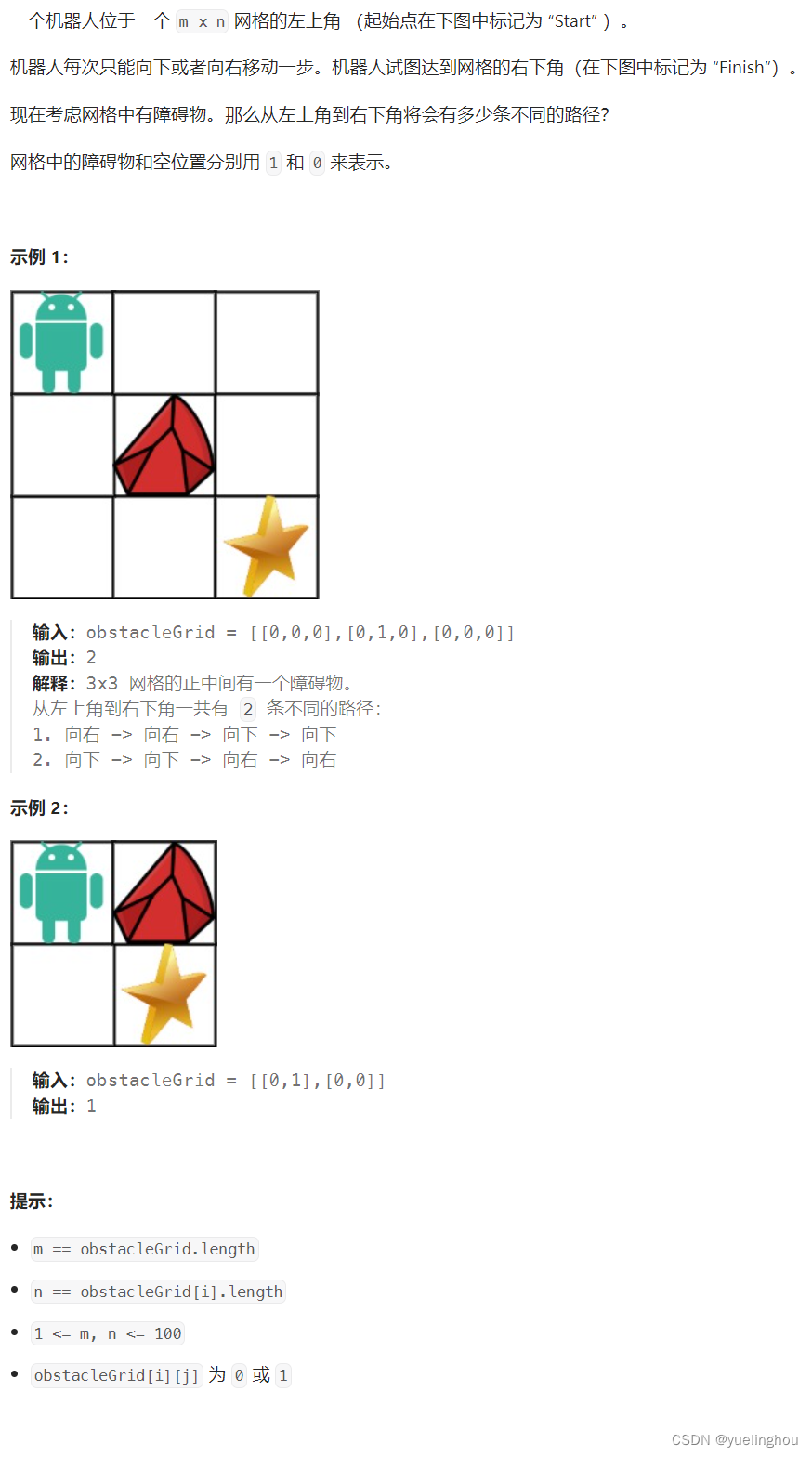
题目解析
这道题的思路和不同路径I 是一样的,只不过我们在填表时,如果遇到了障碍物,那就说明这个位置是无法走到的,我们把这个位置的路径数置为0即可
算法原理
-
状态表示:dp[i][j] 表示到达 (i, j) 位置时,有多少种路径
-
状态转移方程

-
初始化:为了方便后续填表,我们创建的 dp 表要比题目给的矩阵多开一行和多开一列,初始化时要注意以下两点:
- 下标的映射关系
- 要保证后面填表的逻辑正确
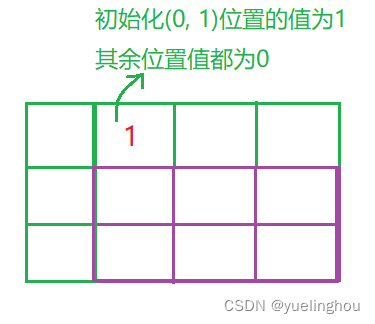
-
填表顺序:从上往下填写每一行,每一行再从左往右填写
-
返回值:dp[m][n]
代码实现
class Solution
{
public:
int uniquePathsWithObstacles(vector<vector<int>>& ob)
{
// 1、建表
size_t m = ob.size();
size_t n = ob[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n));
// 2、初始化
dp[0][1] = 1;
// 3、填表
for (size_t i = 1; i <= m; ++i)
for (size_t j = 1; j <= n; ++j)
if (ob[i - 1][j - 1] != 1)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
3. 礼物的最大价值
算法原理
- 状态表示(根据题目要求+经验):dp[ i ][ j ] 表示走到 (i, j) 时,该位置最多能拿到多少价值的礼物
- 状态转移方程
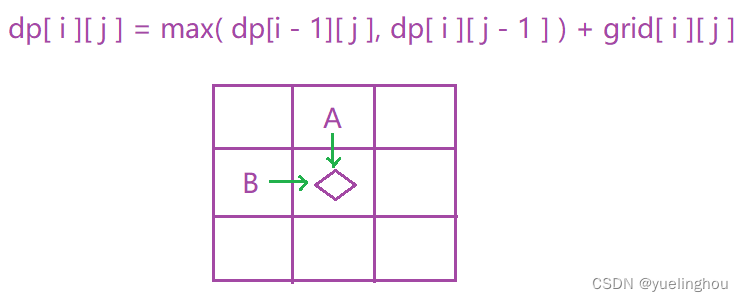
- 初始化
- 填表顺序:从上往下填写每一行,每一行从左往右填写
- 返回值:dp[m][n]
代码编写
class Solution
{
public:
// 1、创建 dp 表
// 2、初始化
// 3、填表
// 4、返回值
int maxValue(vector<vector<int>>& grid)
{
size_t m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (size_t i = 1; i <= m; ++i)
for (size_t j = 1; j <= n; ++j)
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
4. 下降路径最小和
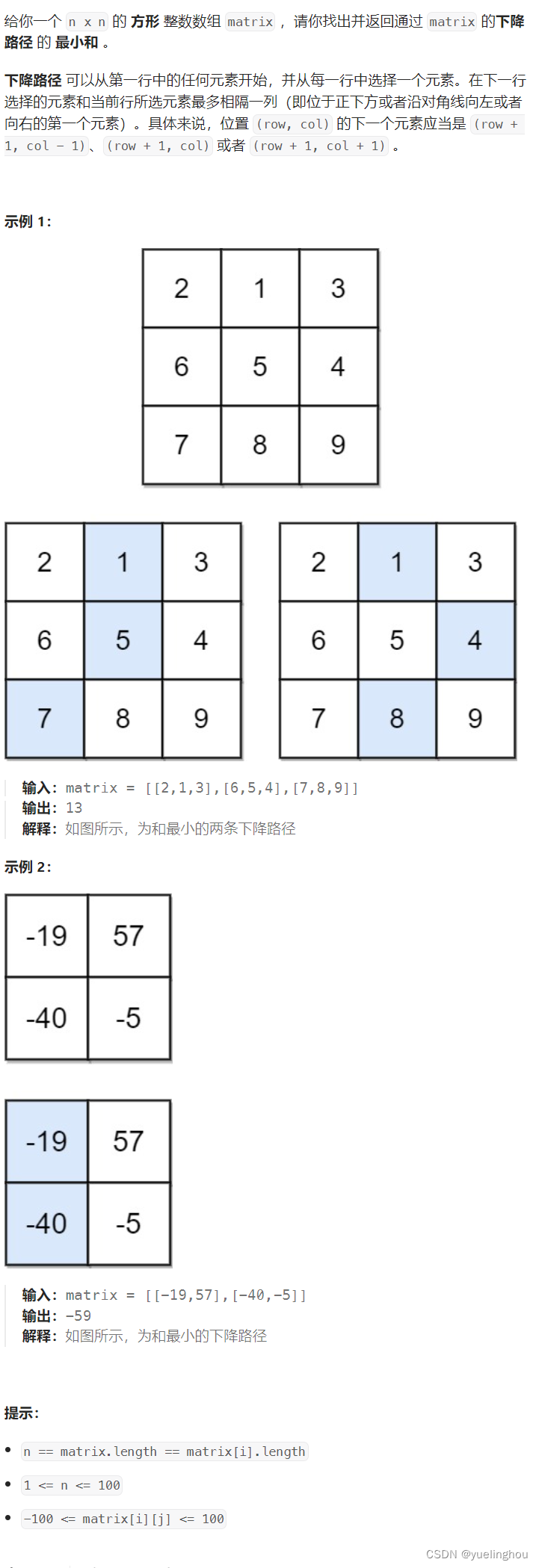
算法原理
-
状态表示(根据经验+题目要求,dp[i][j]表示以 (i, j) 位置为 结尾/起点 时,xxxxxxx…)

-
状态转移方程
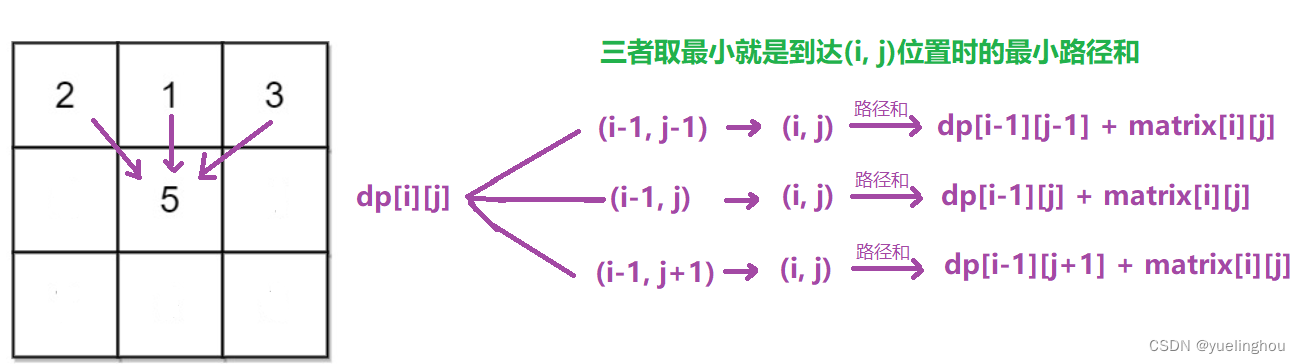
-
初始化(为了保证在填表的时候不越界):
-
填表顺序:每一个元素的值只受最靠近他的上面位置的三个元素的值所影响,所以我们只需保证从上往下填表即可。
-
返回值:最后一行的最小值
代码编写
class Solution
{
public:
int minFallingPathSum(vector<vector<int>>& matrix)
{
// 1、建表
size_t n = matrix.size();
vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));
// 2、初始化
for (size_t j = 0; j < n + 2; ++j)
dp[0][j] = 0;
// 3、填表
for (size_t i = 1; i < n + 1; ++i)
for (size_t j = 1; j < n + 1; ++j)
dp[i][j] = min(min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + matrix[i-1][j-1];
// 4、返回值
int ret = INT_MAX;
for (size_t j = 1; j < n + 1; ++j)
if (dp[n][j] < ret) ret = dp[n][j];
return ret;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
5. 最小路径和
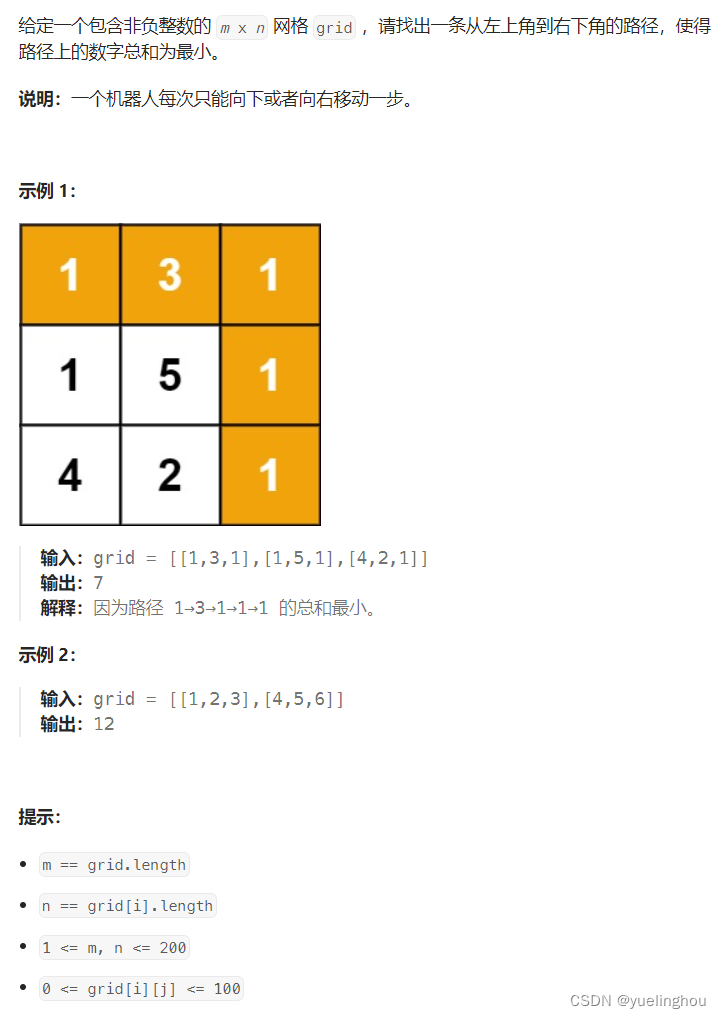
算法原理
-
状态表示(题目 + 经验要求),通常是:以某位置为 结尾/起点 时,巴拉巴拉巴拉…
- dp[i][j]:从起点到达 (i, j) 位置时的最小路径和
-
状态转移方程
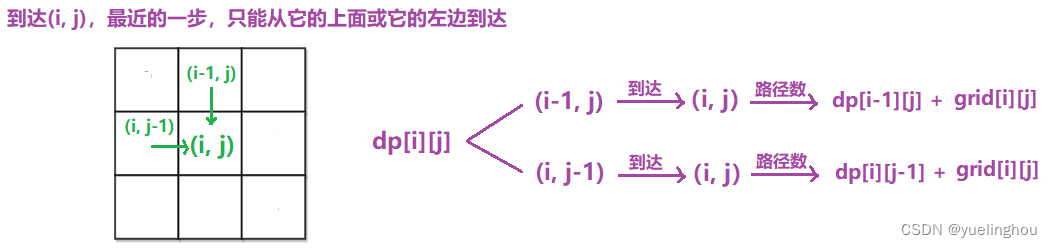
-
初始化(保证填表的时候不越界)

-
填表顺序:从上往下,每一行再从左往右
-
返回值:dp[m][n]
代码编写
class Solution
{
public:
int minPathSum(vector<vector<int>>& grid)
{
// 1、创建 dp 表
size_t m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
// 2、初始化
dp[0][1] = dp[1][0] = 0;
// 3、填表
for (size_t i = 1; i < m + 1; ++i)
for (size_t j = 1; j < n + 1; ++j)
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
6. 地下城游戏

算法原理
- 状态表示(根据 题目要求 + 经验)

- 状态转移方程(以 (i, j) 为起点/终点时,巴拉巴拉巴拉)
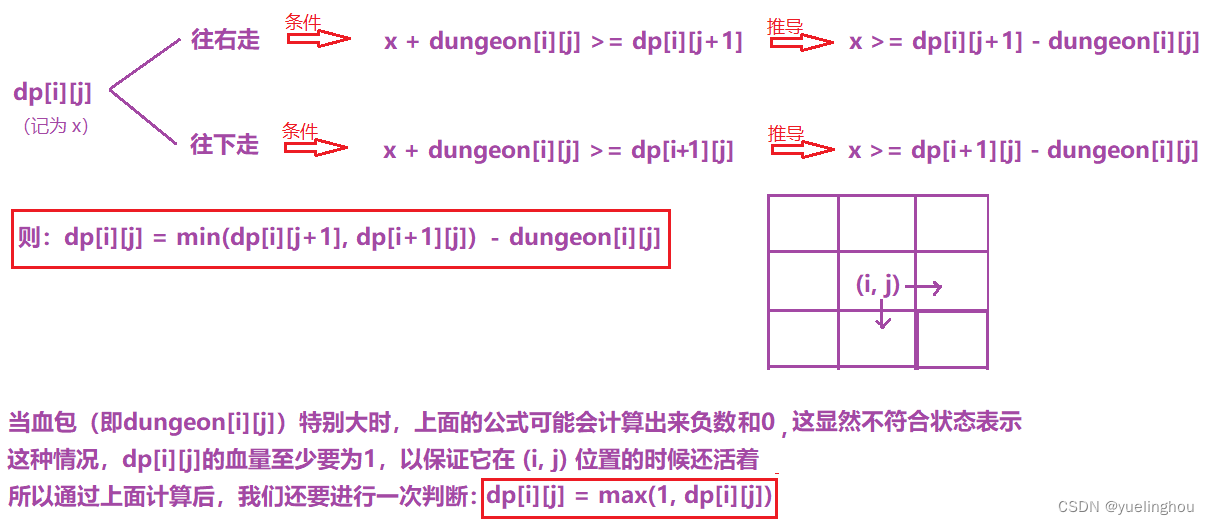
- 初始化

- 填表顺序:从下往上填每一行,每一行再从右往左填
- 返回值:dp[0][0]
代码编写
class Solution
{
public:
int calculateMinimumHP(vector<vector<int>>& dungeon)
{
// 建表
int m = dungeon.size(), n = dungeon[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
// 初始化
dp[m - 1][n] = dp[m][n - 1] = 1;
// 填表
for (int i = m - 1; i >= 0; --i)
{
for (int j = n - 1; j >= 0; --j)
{
dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];
dp[i][j] = max(1, dp[i][j]);
}
}
// 返回值
return dp[0][0];
}
};
/*
- 时间复杂度:O(m*n)
- 空间复杂度:O(m*n)
*/
三. 简单多状态 dp 问题
1. 按摩师

题目解析

算法原理
- 状态表示

- 状态转移方程
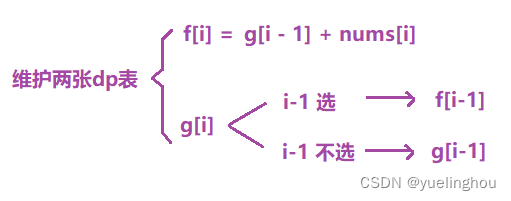
- 初始化

- 填表顺序:从左往右填表,两个表一起填
- 返回值:max(f(n-1), g(n-1))
代码编写
class Solution
{
public:
int massage(vector<int>& nums)
{
// 1、建表
int n = nums.size();
if (n == 0) return 0;
vector<int> f(n), g(n);
// 2、初始化
f[0] = nums[0];
g[0] = 0;
// 3、填表
for (int i = 1; i < n; ++i)
{
f[i] = g[i - 1] + nums[i];
g[i] = max(f[i - 1], g[i - 1]);
}
// 4、返回值
return max(f[n - 1], g[n - 1]);
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
2. 打家劫舍I

算法原理

代码编写
class Solution
{
public:
int rob(vector<int>& nums)
{
// 建表
int n = nums.size();
vector<int> f(n), g(n);
// 初始化
f[0] = nums[0];
// 填表
for (int i = 1; i < n; ++i)
{
f[i] = g[i - 1] + nums[i];
g[i] = max(f[i - 1], g[i - 1]);
}
// 返回值
return max(f[n - 1], g[n - 1]);
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
3. 打家劫舍II

算法原理
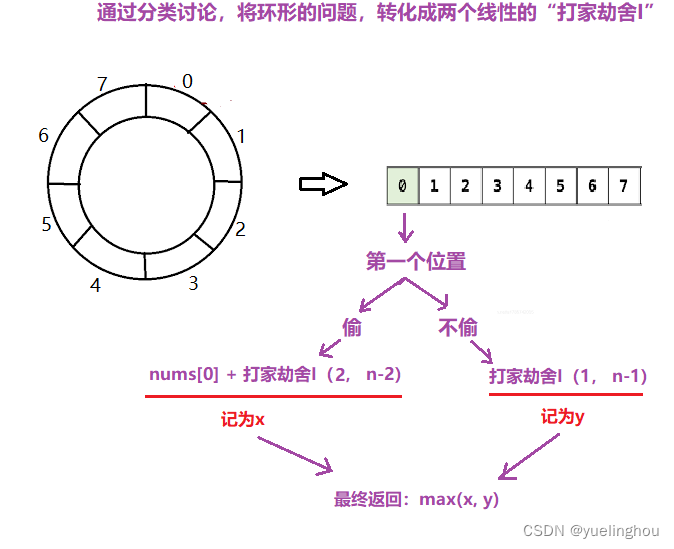
代码编写
class Solution
{
public:
int rob(vector<int>& nums)
{
int n = nums.size();
return max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1));
}
private:
int _rob(vector<int>& nums, int left, int right)
{
if (left > right) return 0;
// 建表
int n = right - left + 1;
vector<int> f(n), g(n);
// 初始化
f[0] = nums[left];
// 填表
for (int i = 1; i < n; ++i)
{
f[i] = g[i - 1] + nums[left + i];
g[i] = max(f[i - 1], g[i - 1]);
}
// 返回值
return max(f[n - 1], g[n - 1]);
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
4. 删除并获得点数

算法原理
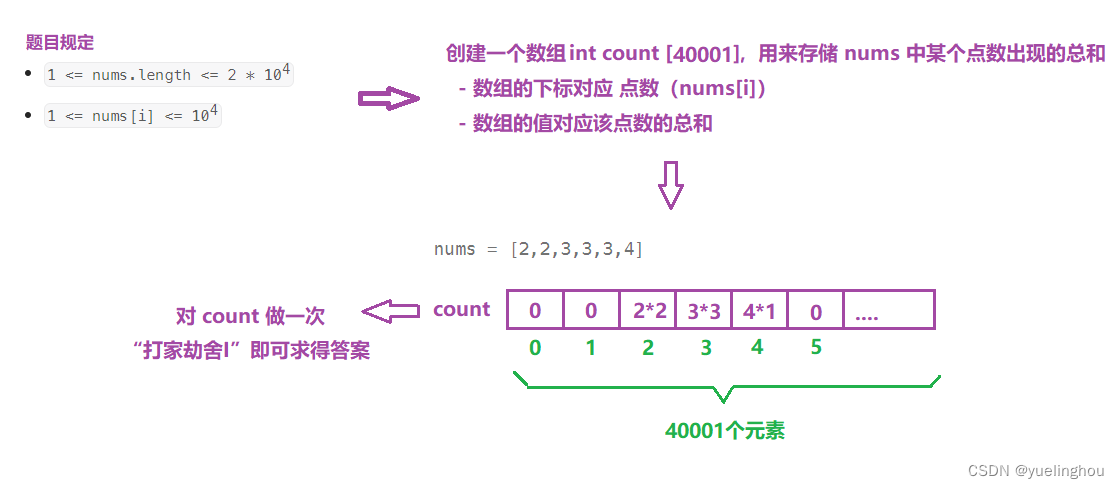
代码编写
class Solution
{
public:
int deleteAndEarn(vector<int>& nums)
{
// 1、建表
vector<int> f(40001);
vector<int> g(40001);
vector<int> count(40001);
// 2、初始化
for(const auto e : nums)
count[e] += e;
// 3、填表
for(int i = 1; i < 40001; ++i)
{
f[i] = count[i] + g[i-1];
g[i] = max(f[i-1], g[i-1]);
}
// 4、返回值
return max(f[40000], g[40000]);
}
};
/*
- 时间复杂度:O(n + 40001)
- 空间复杂度:O(1)
*/
5. 粉刷房子

算法原理
- 状态表示

- 状态转移方程
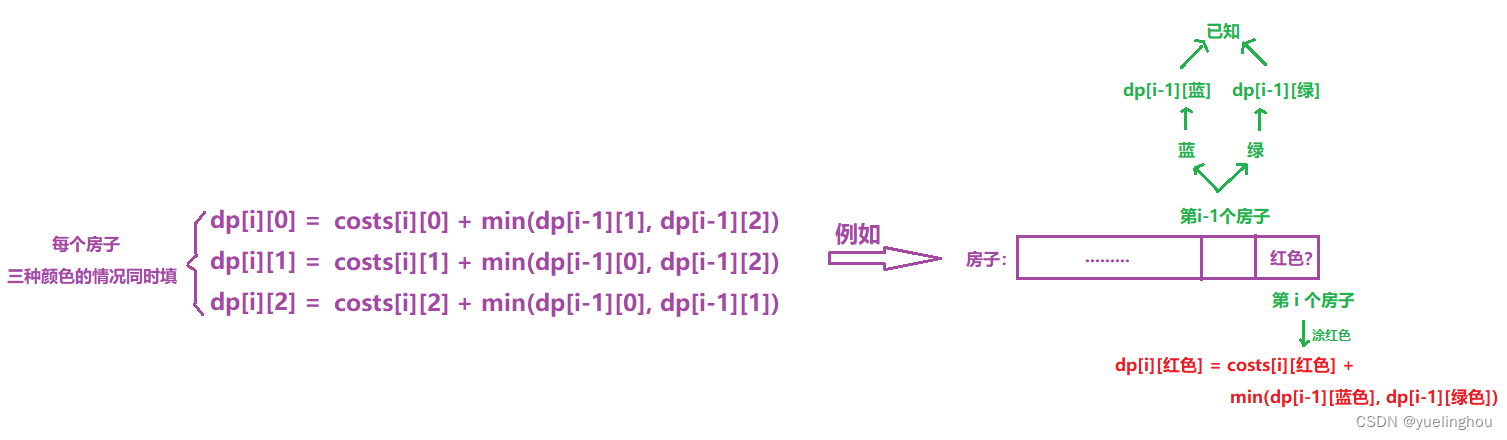
- 初始化
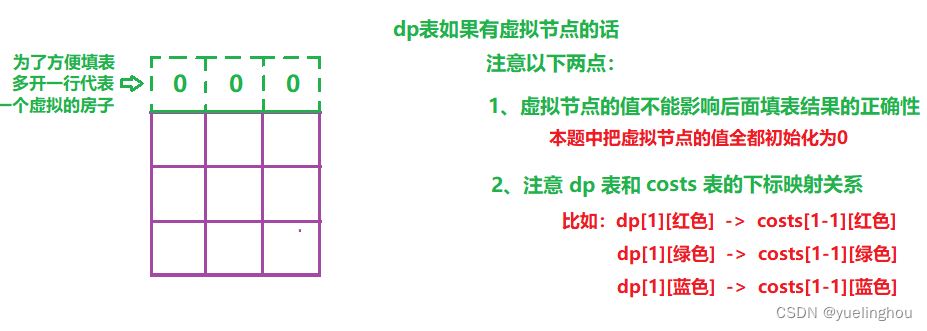
- 填表顺序:从上往下填,每次填好某个房子的三种情况(红色、绿色、蓝色)
- 返回值:因为多开了一行虚拟节点,所以返回
min(dp[n][0], dp[n][1], dp[n][2])
代码编写
class Solution
{
public:
int minCost(vector<vector<int>>& costs)
{
// 1、建表并初始化
int n = costs.size();
vector<vector<int>> dp(n + 1, vector<int>(3));
// 2、填表
for(int i = 1; i <= n; ++i)
{
dp[i][0] = costs[i-1][0] + min(dp[i-1][1], dp[i-1][2]);
dp[i][1] = costs[i-1][1] + min(dp[i-1][0], dp[i-1][2]);
dp[i][2] = costs[i-1][2] + min(dp[i-1][0], dp[i-1][1]);
}
// 3、返回值
return min(dp[n][0], min(dp[n][1], dp[n][2]));
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
6. 买卖股票的最佳时机含冷冻期

算法原理
-
状态表示

-
状态转移方程
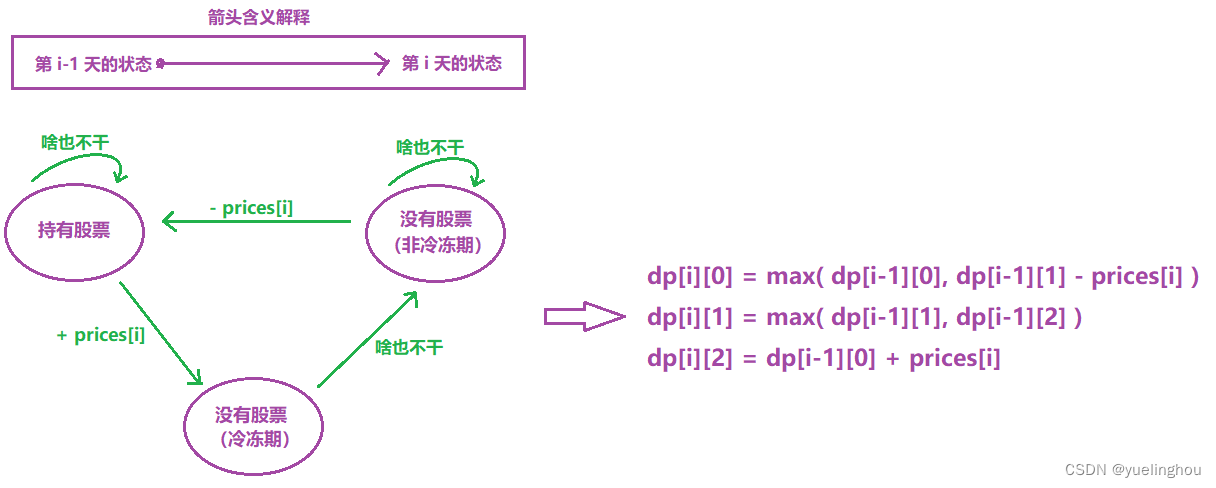
-
初始化:根据状态转移方程可知:想要得到某天结束时,该天三种状态(持有、不持有且处于冷冻期、不持有但不处于冷冻期)各自的最大利润,则需要知道前一天的三种状态的值,所以我们只需要初始化好第一天三种状态的结果,然后填表时从第二天开始填即可

-
填表顺序:从上往下填,填写每一天的三种状态各自的最大利润
-
返回值

代码编写
class Solution
{
public:
int maxProfit(vector<int>& prices)
{
// 1、建表
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3));
// 2、初始化
dp[0][0] = -prices[0];
// 3、填表
for (int i = 1; i < n; ++i)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i];
}
// 4、返回值
return max(dp[n - 1][1], dp[n - 1][2]);
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
7. 买卖股票的最佳时机含手续费

算法原理
-
状态表示
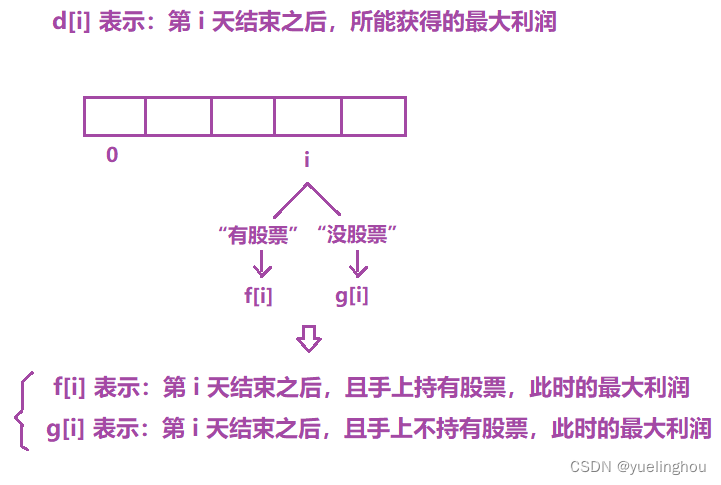
-
状态转移方程
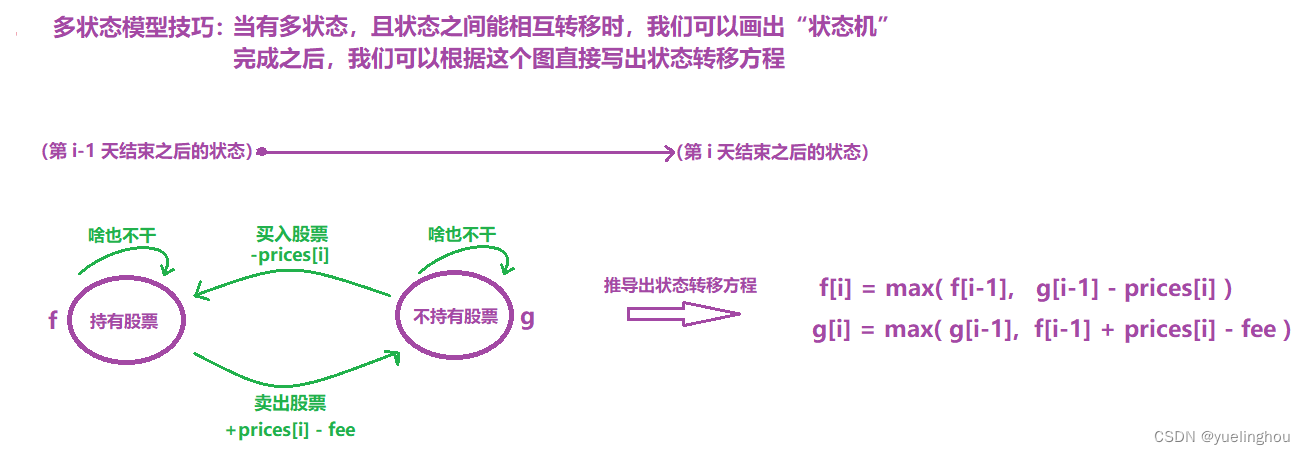
-
初始化:f[0] = -prices[i]、g[0] = 0
-
填表顺序:从左往右,两张表一起填
-
返回值:最终返回值的话,就不考虑 f[n-1] 了,因为最后一天还持有股票的话:要么就是当天新买的,要么就是之前买的,但是一直没有卖出。这两种情况都不可能是最大利润,所以直接返回 g[n-1] 即可。
代码编写
class Solution
{
public:
int maxProfit(vector<int>& prices, int fee)
{
// 1、建表
int n = prices.size();
vector<int> f(n), g(n);
// 2、初始化
f[0] = -prices[0];
// 3、填表
for(int i = 1; i < n; ++i)
{
f[i] = max(f[i-1], g[i-1] - prices[i]);
g[i] = max(g[i-1], f[i-1] + prices[i] - fee);
}
// 4、返回值
return g[n-1];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
8. 买卖股票的最佳时机 III

算法原理
-
状态表示
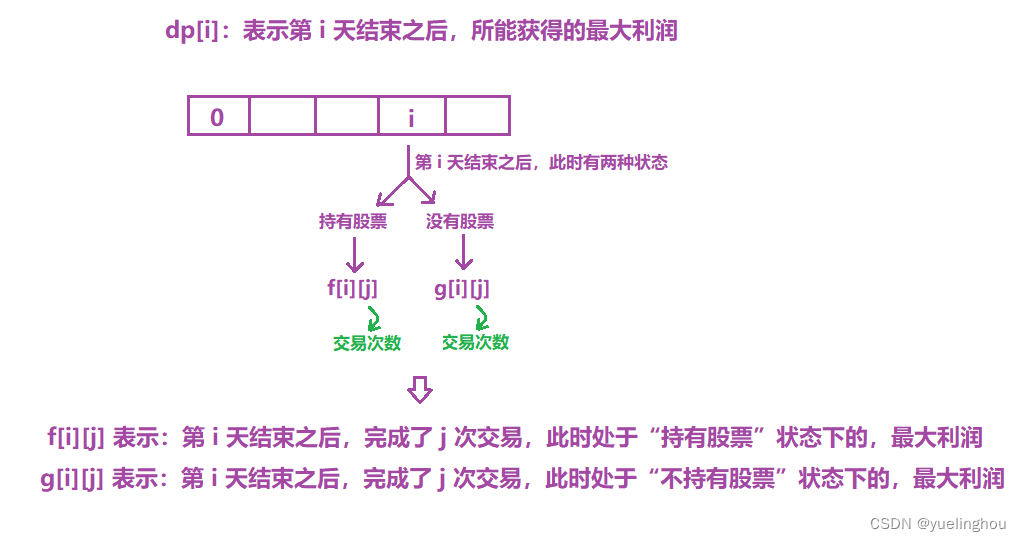
-
状态转移方程
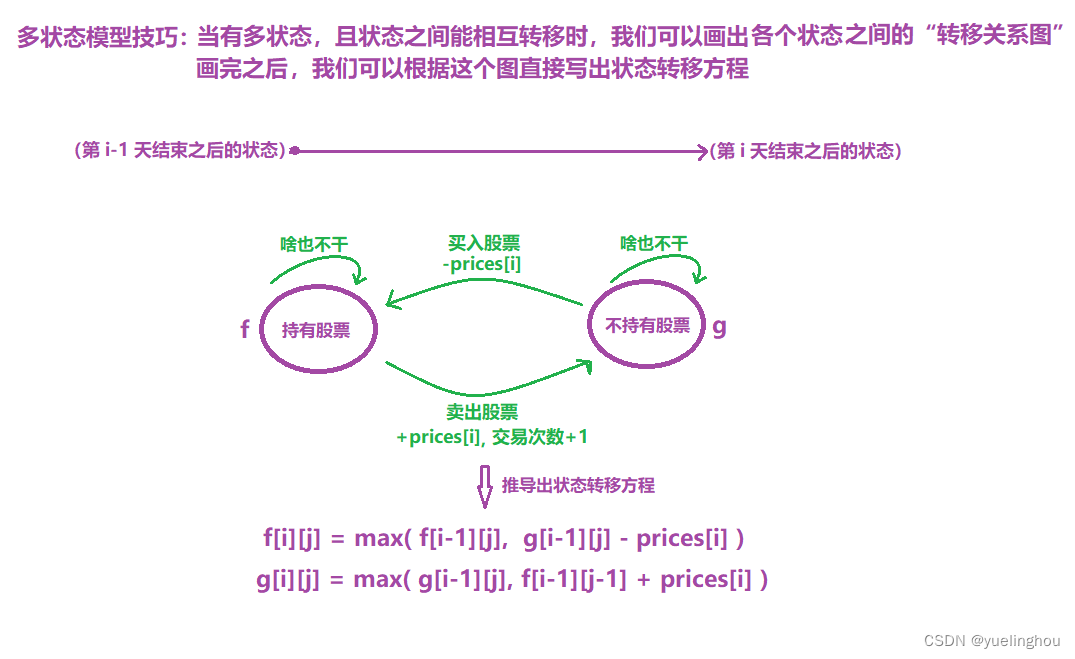
-
初始化
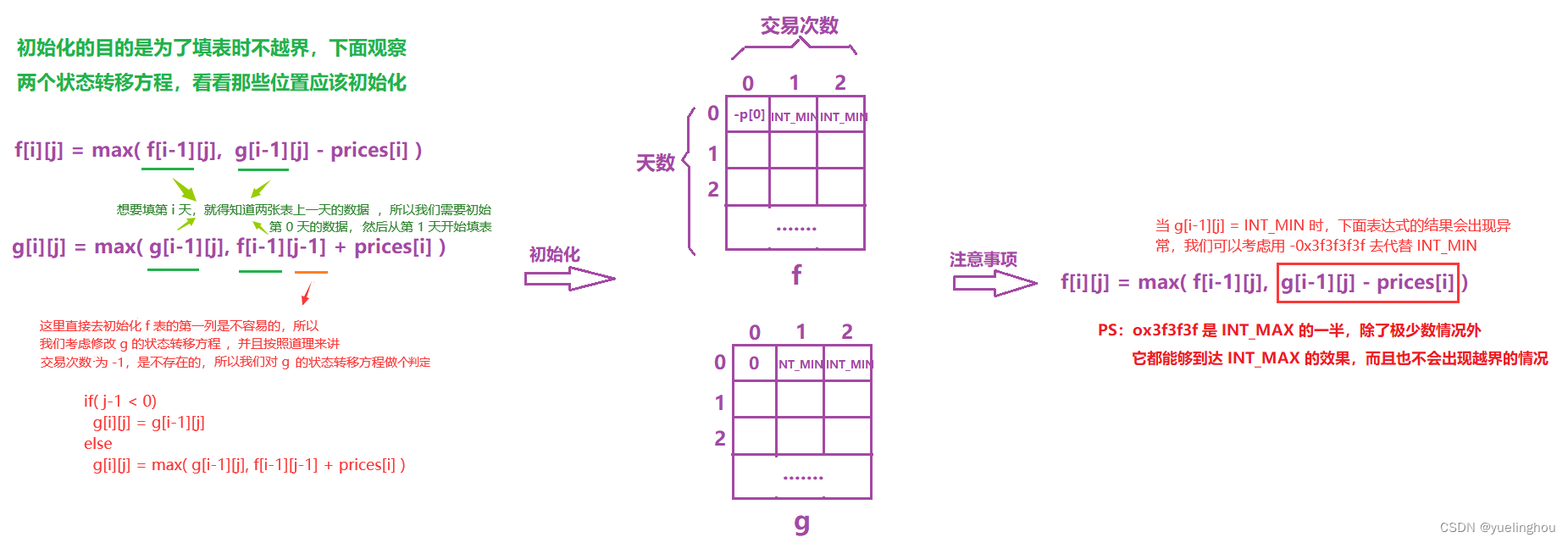
-
填表顺序:从 i=1 开始,从下往上填写每一行,每一行从左往右,两张表一起填
-
返回值:找到并返回 g 表最后一行的最大值(可能是零笔交易出最大值,也可能是一笔或两笔)
代码编写
class Solution
{
public:
const int INF = 0x3f3f3f3f;
int maxProfit(vector<int>& prices)
{
// 1、建表
int n = prices.size();
vector<vector<int>> f(n, vector<int>(3, -INF));
auto g(f);
// 2、初始化
f[0][0] = -prices[0], g[0][0] = 0;
// 3、填表
for (int i = 1; i < n; ++i)
{
for (int j = 0; j < 3; ++j)
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
if (j - 1 < 0)
g[i][j] = g[i - 1][j];
else
g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
}
}
// 4、返回值
int ret = -INF;
for (int j = 0; j < 3; ++j)
{
if (g[n - 1][j] > ret)
{
ret = g[n - 1][j];
}
}
return ret;
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
9. 买卖股票的最佳时期IV

算法原理
- 状态表示
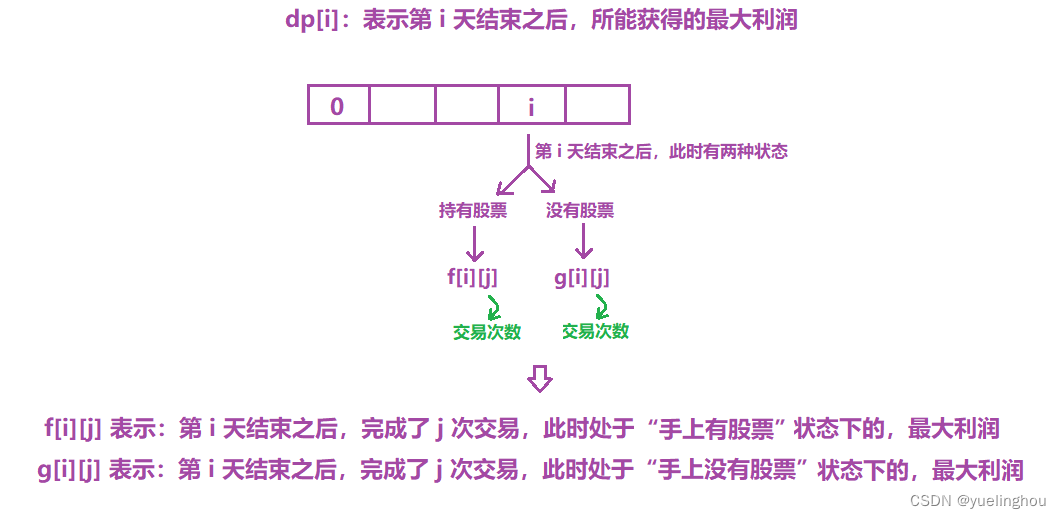
- 状态转移方程
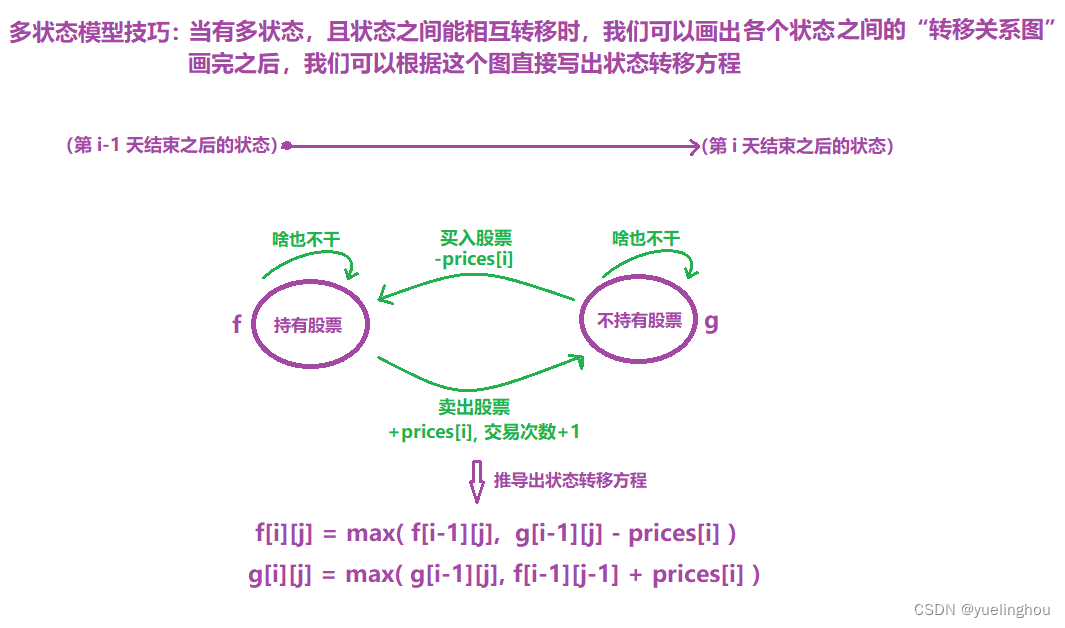
- 初始化
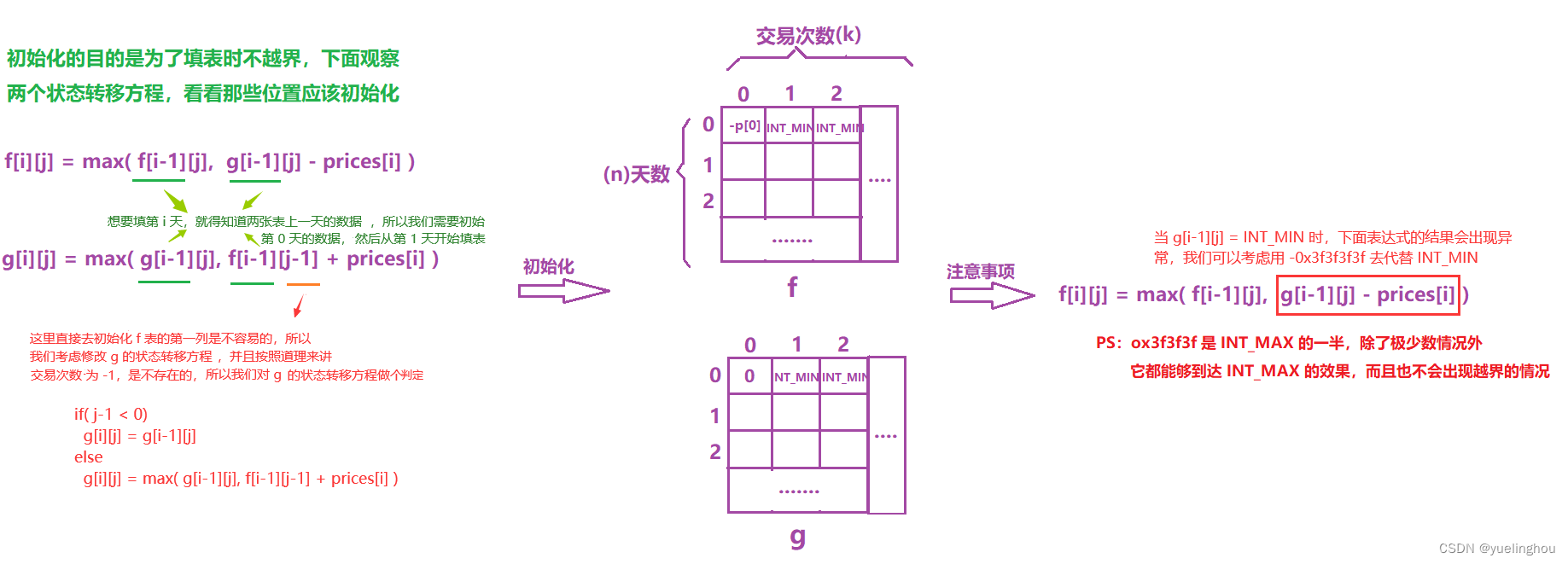
- 填表顺序:从 i=1 开始,从下往上填写每一行,每一行从左往右,两张表一起填
- 返回值:找到并返回 g 表最后一行的最大值
代码编写
class Solution
{
public:
const int INF = 0x3f3f3f3f;
int maxProfit(int k, vector<int>& prices)
{
// 1、建表
int n = prices.size();
vector<vector<int>> f(n, vector<int>(k + 1, -INF));
auto g(f);
// 2、初始化
f[0][0] = -prices[0], g[0][0] = 0;
// 3、填表
for (int i = 1; i < n; ++i)
{
for (int j = 0; j < k + 1; ++j)
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
if (j - 1 < 0)
g[i][j] = g[i - 1][j];
else
g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
}
}
// 4、返回值
int ret = -INF;
for (int j = 0; j < k + 1; ++j)
{
if (g[n - 1][j] > ret)
{
ret = g[n - 1][j];
}
}
return ret;
}
};
/*
- 时间复杂度:O(n*k)
- 空间复杂度:O(n*k)
*/
四. 子数组系列
1. 最大子数组和

算法原理
- 状态表示
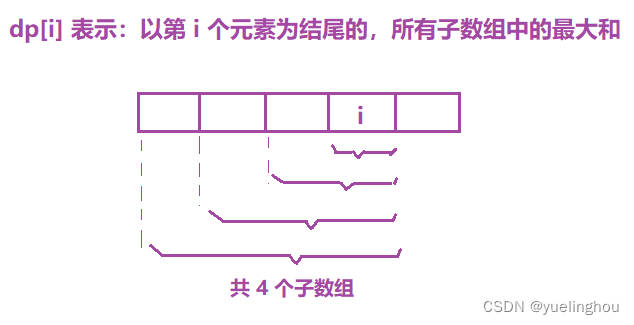
- 状态转移方程
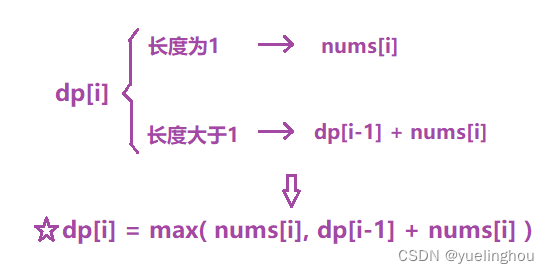
- 初始化

- 填表顺序:从左往右
- 返回值:dp表中最大值
代码编写
class Solution
{
public:
const int INF = 0x3f3f3f3f;
int maxSubArray(vector<int>& nums)
{
// 1、建表
int n = nums.size();
vector<int> dp(n + 1);
// 2、初始化
dp[0] = -INF;
// 2、填表
for (int i = 1; i <= n; ++i)
{
dp[i] = max(nums[i-1], dp[i - 1] + nums[i-1]);
}
// 3、返回值
return *max_element(dp.begin(), dp.end());
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
2. 环形子数组的最大和

思路分析

算法原理
-
状态表示
- f[i] 表示:以 i 为结尾的所有子数组中的最大和
- g[i] 表示:以 i 为结尾的所有子数组中的最小和
-
状态转移方程

-
初始化

-
填表顺序:从左往右,两张表一起填
-
返回值

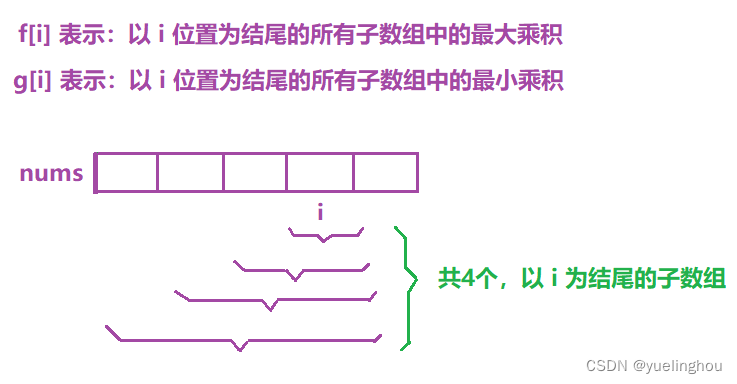
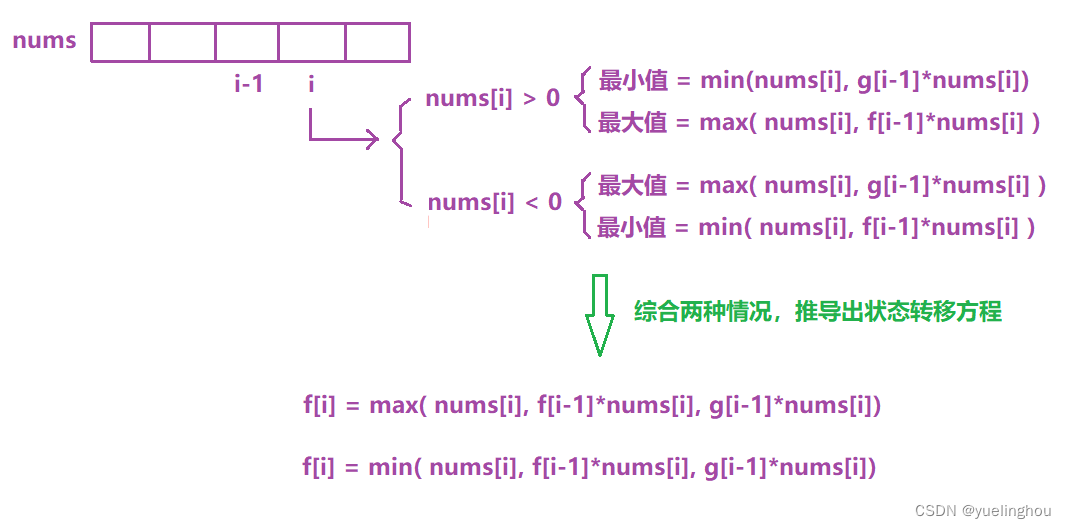
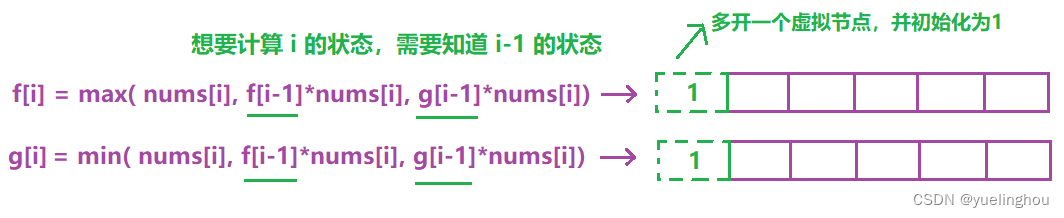
3. 乘积最大子数组

算法原理
- 状态表示
- 状态转移方程
- 初始化
- 填表顺序:从左往右,两张表一起填
- 返回值:f 表中的最大值(注意虚拟节点的值不算在内)
代码编写
class Solution
{
public:
int maxProduct(vector<int>& nums)
{
// 1、建表
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
// 2、初始化
f[0] = g[0] = 1;
// 3、填表
for (int i = 1; i <= n; ++i)
{
f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));
g[i] = min(nums[i - 1], min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));
}
// 4、返回值
return *max_element(f.begin() + 1, f.end());
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
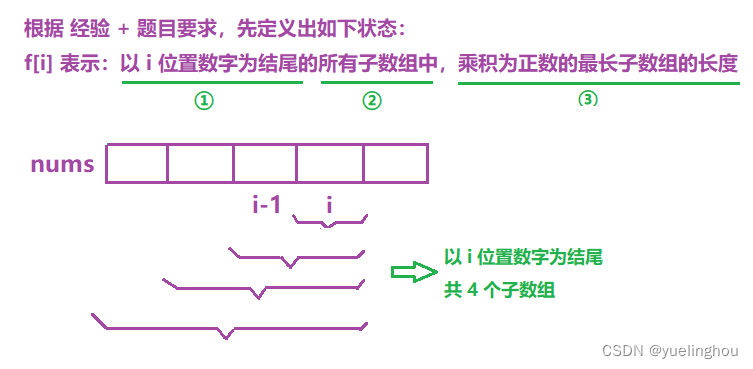
4. 乘积为正数的最长子数组长度

算法原理
- 状态表示
- 状态转移方程
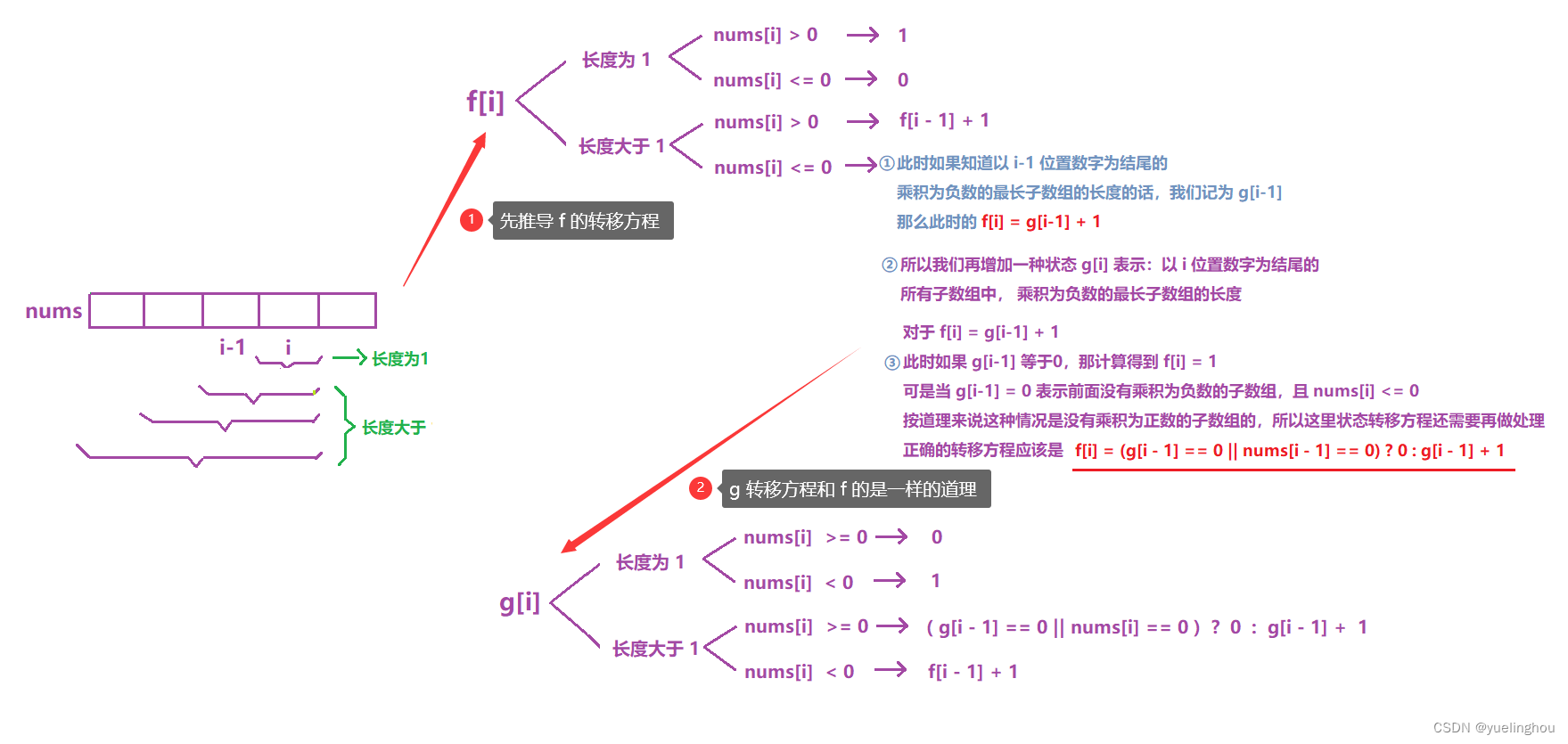
- 初始化

- 填表顺序:从左往右,两张表一起填
- 返回值:f 表中的最大值(注意虚拟节点的值不算在内)
代码编写
class Solution
{
public:
int getMaxLen(vector<int>& nums)
{
// 1、建表 && 初始化
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
// 2、填表
for(int i = 1; i <= n; ++i)
{
if(nums[i - 1] > 0)
f[i] = f[i - 1] + 1;
else
f[i] = (g[i - 1] == 0 || nums[i - 1] == 0) ? 0 : g[i - 1] + 1;
if(nums[i - 1] >= 0)
g[i] = (g[i - 1] == 0 || nums[i - 1] == 0) ? 0 : g[i - 1] + 1;
else
g[i] = f[i - 1] + 1;
}
// 3、返回值
return *max_element(f.begin() + 1, f.end());
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
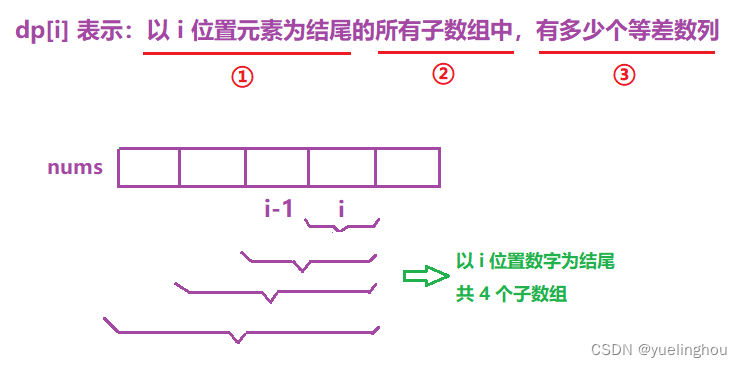
5. 等差数列划分

算法原理
- 状态表示
- 状态转移方程
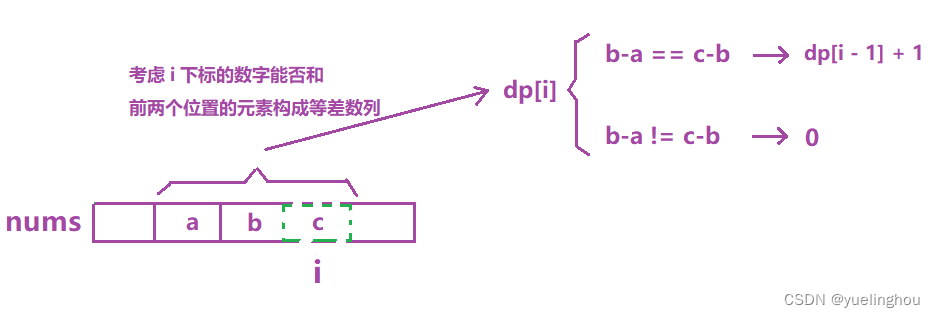
- 初始化

- 填表顺序:从左往右
- 返回值:dp 表中所有元素之和
代码编写
class Solution
{
public:
int numberOfArithmeticSlices(vector<int>& nums)
{
// 1、建表 和 初始化
int n = nums.size();
vector<int> dp(n);
// 2、填表
int ret = 0;
for(int i = 2; i < n; ++i)
{
nums[i - 1] - nums[i - 2] == nums[i] - nums[i - 1] ? dp[i] = dp[i - 1] + 1 : dp[i] = 0;
ret += dp[i];
}
// 3、返回值
return ret;
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
6. 最长湍流子数组
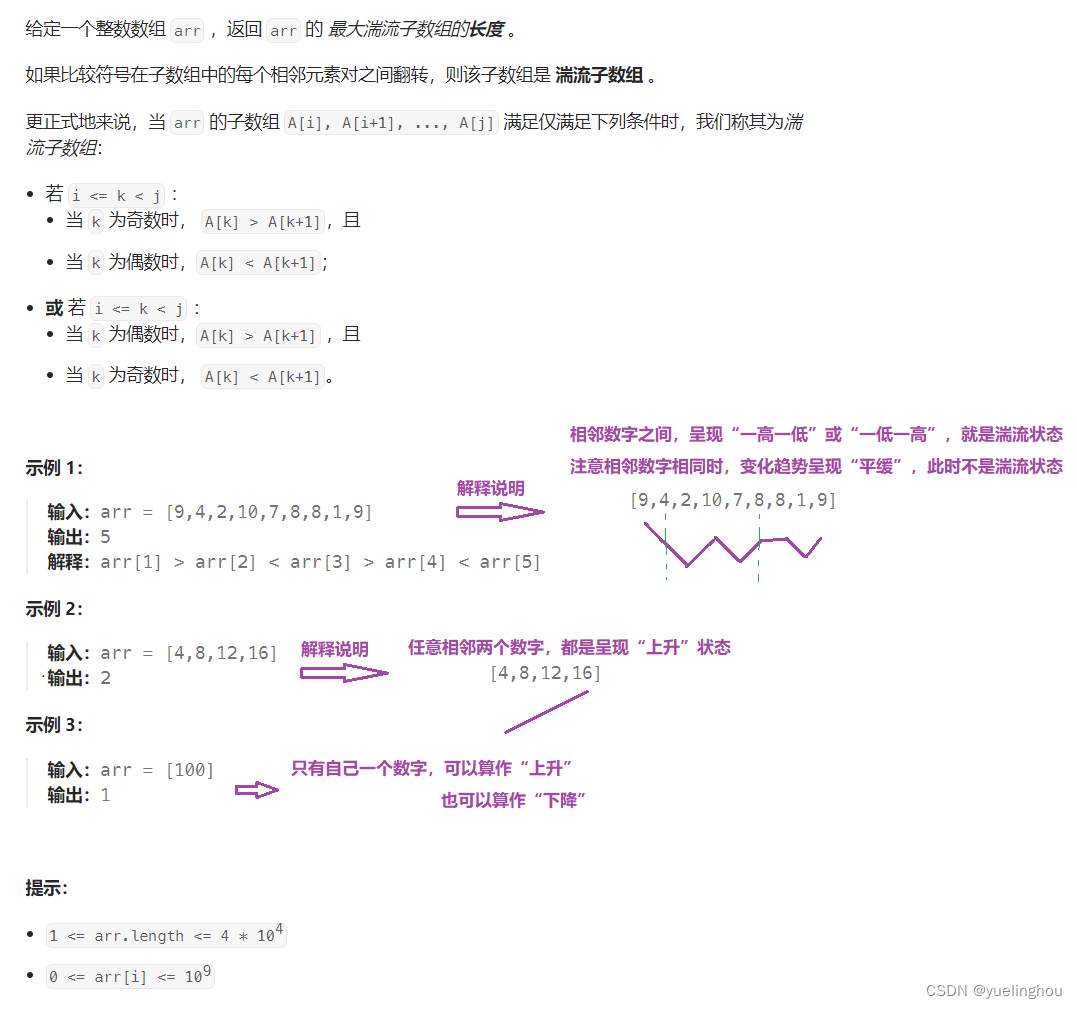
算法原理
- 状态表示
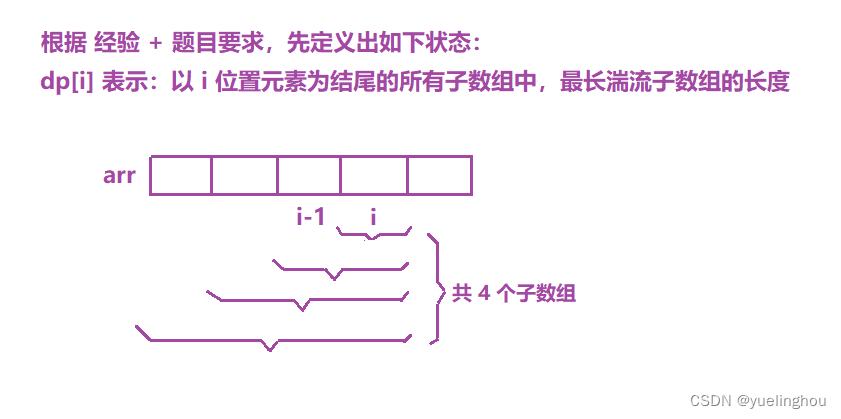
- 状态转移方程
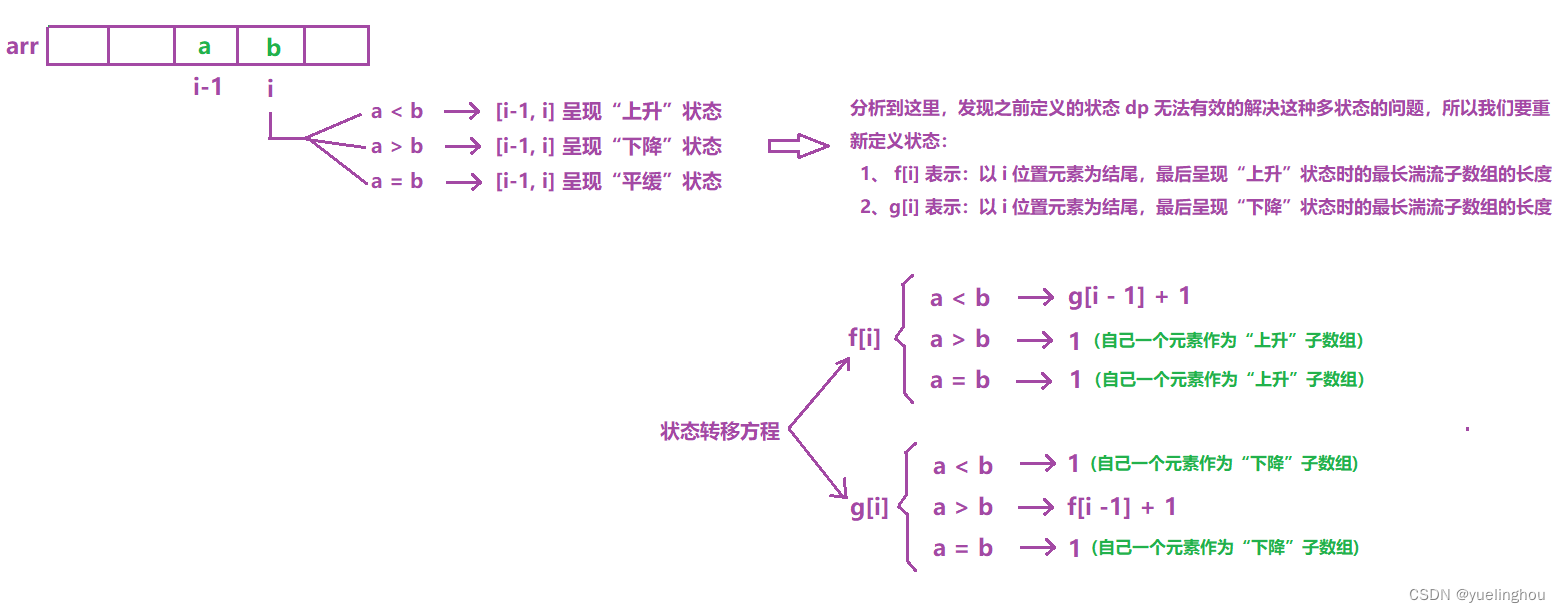
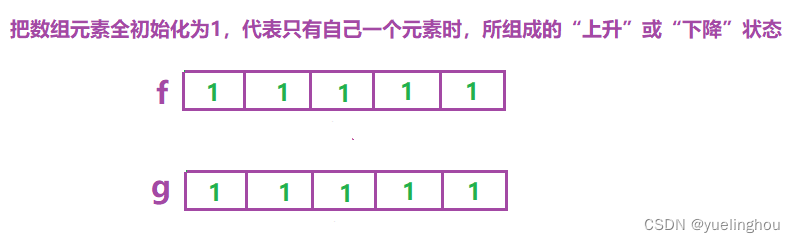
- 初始化
- 填表顺序:从左往右,两张表一起填
- 返回值:f、g 表里面的最大值
代码编写
class Solution
{
public:
int maxTurbulenceSize(vector<int>& arr)
{
// 1、建表 && 初始化
int n = arr.size();
vector<int> f(n, 1), g(n, 1);
// 2、填表
for (int i = 1; i < n; ++i)
{
if (arr[i - 1] < arr[i]) f[i] = g[i - 1] + 1;
if (arr[i - 1] > arr[i]) g[i] = f[i - 1] + 1;
}
// 3、返回值
return max(*max_element(f.begin(), f.end()), *max_element(g.begin(), g.end()));
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
7. 单词拆分

算法原理
- 状态表示

- 状态转移方程

- 初始化

- 填表顺序:从左往右
- 返回值:dp[n]
代码编写
class Solution
{
public:
bool wordBreak(string s, vector<string>& wordDict)
{
// 1、建表
int n = s.size();
vector<int> dp(n + 1);
// 2、初始化
dp[0] = true;
s = ' ' + s;
// 3、填表
for(int i = 1; i <= n; ++i)
{
for(int j = i; j >= 1; --j)
{
if(dp[j - 1] &&
find(wordDict.begin(), wordDict.end(), s.substr(j, i - j + 1)) != wordDict.end())
{
dp[i] = true;
break;
}
}
}
// 4、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n^2)
*/
8. 环绕字符串中唯一的子字符串

算法原理
- 状态表示
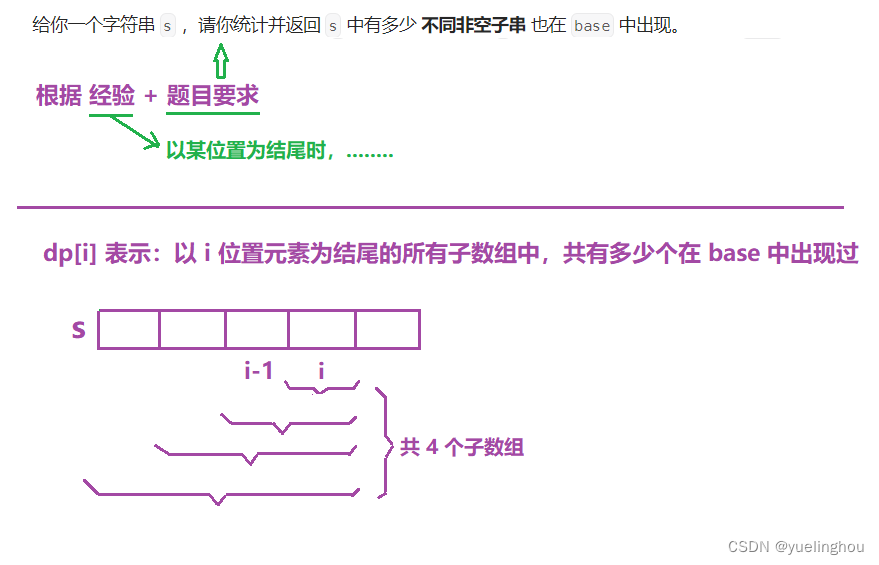
- 状态转移方程
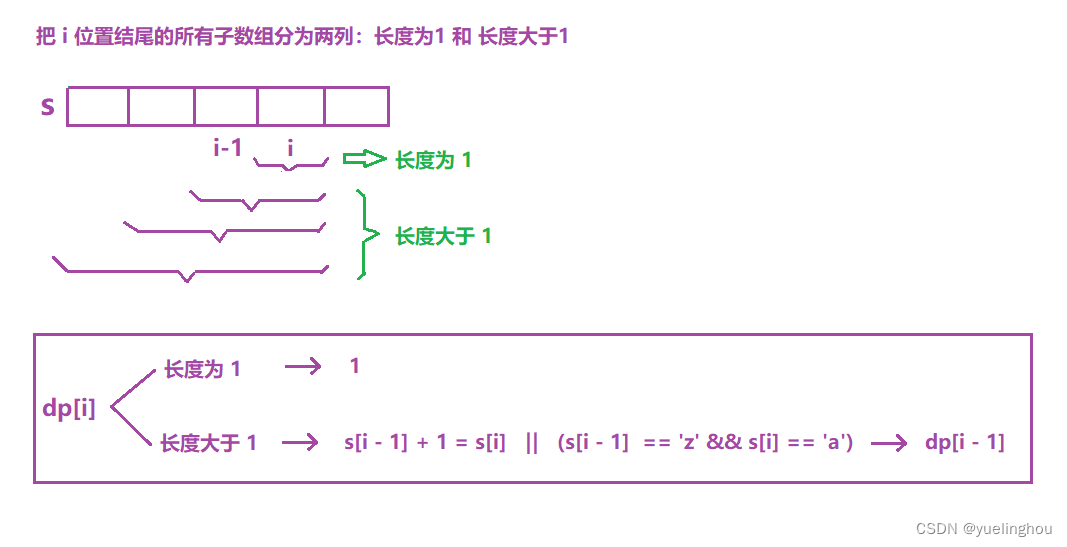
- 初始化:因为每一个元素单独也属于 base,所以把 dp 表里的值全都初始化为 1
- 填表顺序:从左往右填表
- 返回值

代码编写
class Solution
{
public:
int findSubstringInWraproundString(string s)
{
// 1、建表 && 初始化
int n = s.size();
vector<int> dp(n, 1);
// 2、填表
for(int i = 1; i < n; ++i)
if(s[i - 1] + 1 == s[i] || (s[i - 1] == 'z' && s[i] == 'a'))
dp[i] += dp[i - 1];
// 3、返回值
vector<int> count(26);
for(int i = 0; i < n; ++i) count[s[i] - 'a'] = max(count[s[i] - 'a'], dp[i]);
int ret = 0;
for(const auto e : count) ret += e;
return ret;
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
五. 子序列问题
| 概念 | 定义 | 要求 | 范围 |
|---|---|---|---|
| 子数组 | 一个或连续多个数组中的元素组成一个子数组(子数组最少包含一个元素) | 必须要相邻 | 更小 |
| 子序列 | 子序列就是在原来序列中找出一部分组成的序列(子序列不一定连续) | 必须要保证相对顺序 | 更大 |
1. 最长递增子序列

算法原理:
- 状态表示

- 状态转移方程

- 初始化:表里的元素全部初始化为1,表示最基本的情况,即只有自己一个数字构成的最长严格递增子序列。
- 填表顺序:从左往右
- 返回值:dp 表中的最大值
代码编写
class Solution
{
public:
int lengthOfLIS(vector<int>& nums)
{
// 1、建表 && 初始化
int n = nums.size();
vector<int> dp(n, 1);
// 2、填表
for(int i = 1; i < n; ++i)
for(int j = 0; j < i; ++j)
if(nums[j] < nums[i])
dp[i] = max(dp[i], 1 + dp[j]);
// 3、返回值
return *max_element(dp.begin(), dp.end());
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
*/
2. 摆动序列

算法原理
-
状态表示

-
状态转移方程

-
初始化:把 f、g 表中的元素全都初始化为 1,表示最基本的情况,即只有一个数字构成的摆动序列。
-
填表顺序:从左往右,两张表一起填
-
返回值:两张表中所有元素的最大值
代码编写
class Solution
{
public:
int wiggleMaxLength(vector<int>& nums)
{
// 1、建表 && 初始化
int n = nums.size();
vector<int> f(n, 1), g(n, 1);
// 2、填表
for(int i = 1; i < n; ++i)
{
for(int j = 0; j < i; ++j)
{
if(nums[j] < nums[i]) f[i] = max(f[i], g[j] + 1);
if(nums[j] > nums[i]) g[i] = max(g[i], f[j] + 1);
}
}
// 3、返回值
return max(*max_element(f.begin(), f.end()), *max_element(g.begin(), g.end()));
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
*/
3. 最长递增子序列的个数

算法原理
在讲解算法原理之前,我们先看一个小 demo:

了解了上面算法的思想后,回到本题:
- 状态表示

- 状态转移方程

- 初始化:两张表的元素都初始化为 1,表示最基本的,只有自己一个元素构成的最长递增子序列的情况。
- 填表顺序:从左往右,两张表一起填
- 返回值:在填表之前就创建两个变量,用来统计最长长度和该长度出现的次数,然后填表阶段更新它们的值,最后返回出现次数即可。
代码编写
class Solution
{
public:
int findNumberOfLIS(vector<int>& nums)
{
// 1、建表 && 初始化
int n = nums.size();
vector<int> len(n, 1), count(n, 1);
// 2、填表
int retLen = 1, retCount = 1;
for(int i = 1; i < n; ++i)
{
for(int j = 0; j < i; ++j)
{
if(nums[j] < nums[i])
{
if(len[j] + 1 == len[i]) count[i] += count[j];
else if(len[j] + 1 > len[i]) len[i] = len[j] + 1, count[i] = count[j];
}
}
if(len[i] > retLen) retLen = len[i], retCount = count[i];
else if(len[i] == retLen) retCount += count[i];
}
// 返回值
return retCount;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
*/
4. 最长数对链

算法原理
- 预处理

- 状态表示:dp[i] 表示 以 i 位置元素为结尾的所有数对链中,最长的数对链的长度。
- 状态转移方程
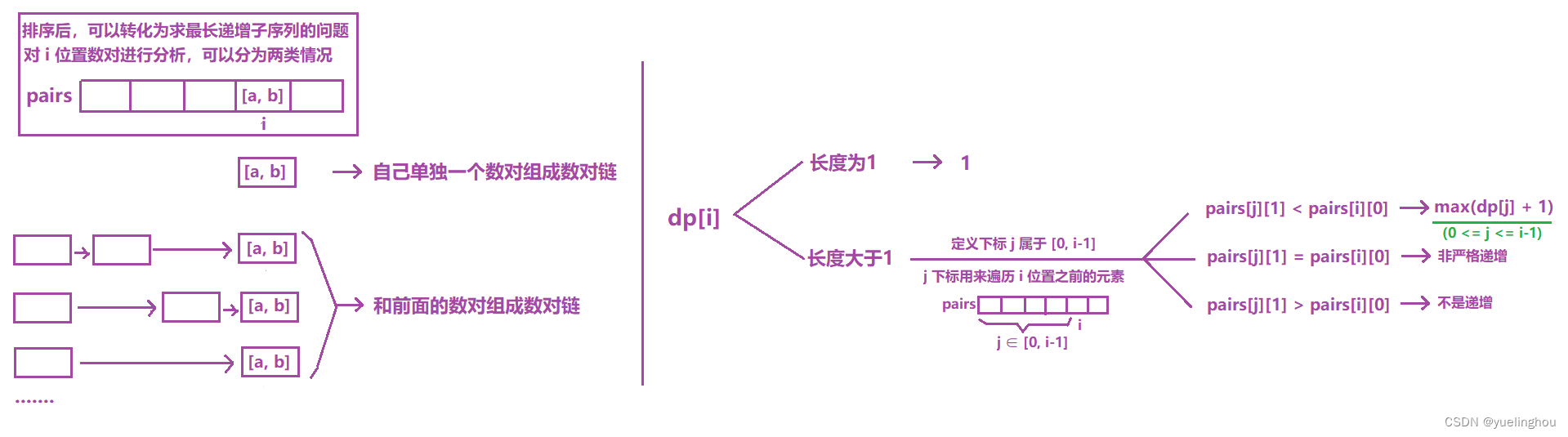
- 初始化:dp 表中的元素都初始化为 1,表示最基本的,只有自己一个数对构成的数对链的长度。
- 填表顺序:从左往右
- 返回值:dp 表中的最大值
代码编写
class Solution
{
public:
int findLongestChain(vector<vector<int>>& pairs)
{
// 1、预处理
sort(pairs.begin(), pairs.end());
// 2、建表
int n = pairs.size();
vector<int> dp(n, 1);
// 3、填表
for(int i = 1; i < n; ++i)
for(int j = 0; j < i; ++j)
if(pairs[j][1] < pairs[i][0])
dp[i] = max(dp[i], dp[j] + 1);
// 4、返回值
return *max_element(dp.begin(), dp.end());
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
*/
5. 最长定差子序列

算法原理
-
状态表示

-
状态转移方程
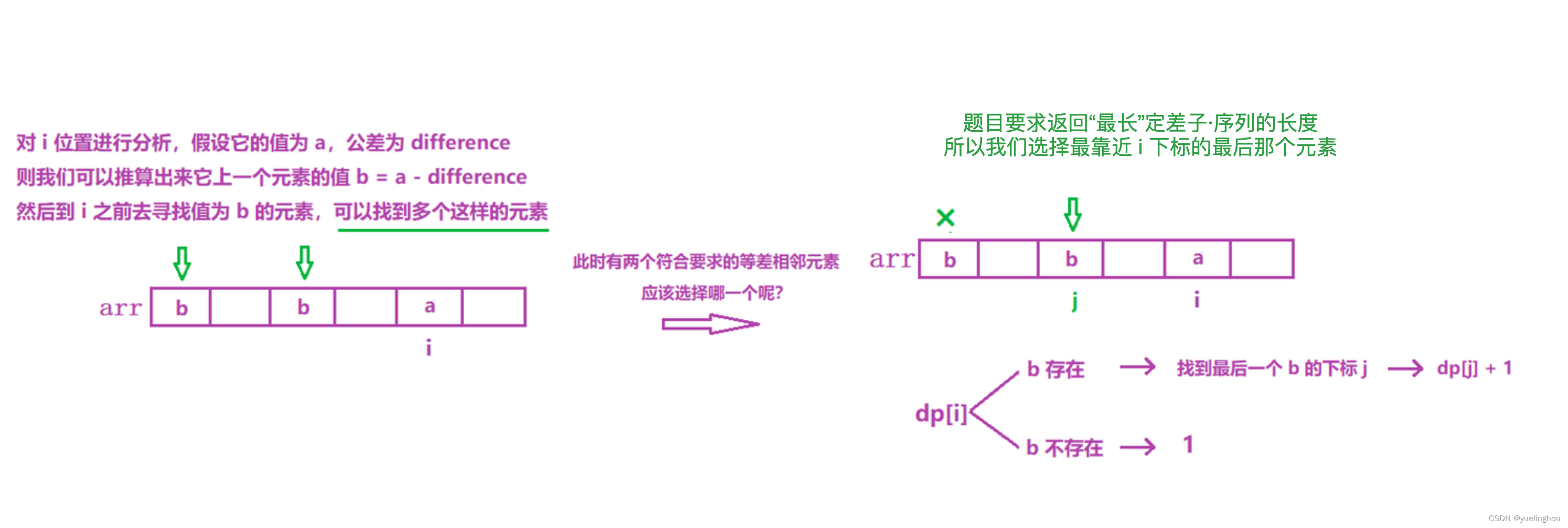
-
初始化

-
填表顺序:从左往右
-
返回值:dp 表中的最大值,注意 dp 表是作为哈希表的 value
代码编写
class Solution
{
public:
int longestSubsequence(vector<int>& arr, int difference)
{
// 1、建表
unordered_map<int, int> hash;
// 2、初始化
hash[arr[0]] = 1;
// 3、填表
int ret = INT_MIN;
for (int i = 1; i < arr.size(); ++i)
{
hash[arr[i]] = hash[arr[i] - difference] + 1;
ret = max(ret, hash[arr[i]]);
}
// 4、返回值
return ret;
}
};
/*
- 时间复杂度:O(n)
- 空间复杂度:O(n)
*/
6. 最长的斐波那契子序列的长度

算法原理
- 状态表示

- 状态转移方程

- 初始化
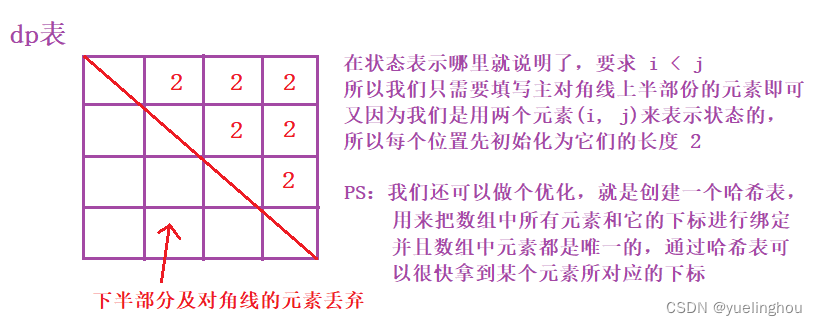
- 填表顺序

- 返回值

代码编写
class Solution
{
public:
int lenLongestFibSubseq(vector<int>& arr)
{
// 1、建表
int n = arr.size();
vector<vector<int>> dp(n, vector<int>(n, 2));
// 2、初始化
unordered_map<int, int> hash;
for(int i = 0; i < n; ++i) hash[arr[i]] = i;
// 3、填表
int ret = INT_MIN;
for(int j = 0; j < n; ++j)
{
for(int i = 0; i < j; ++i)
{
int a = arr[j] - arr[i];
if(hash.count(a) && a < arr[i])
dp[i][j] = dp[hash[a]][i] + 1;
ret = max(ret, dp[i][j]);
}
}
// 4、返回值
return ret == 2 ? 0 : ret;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
7. 最长等差数列

算法原理
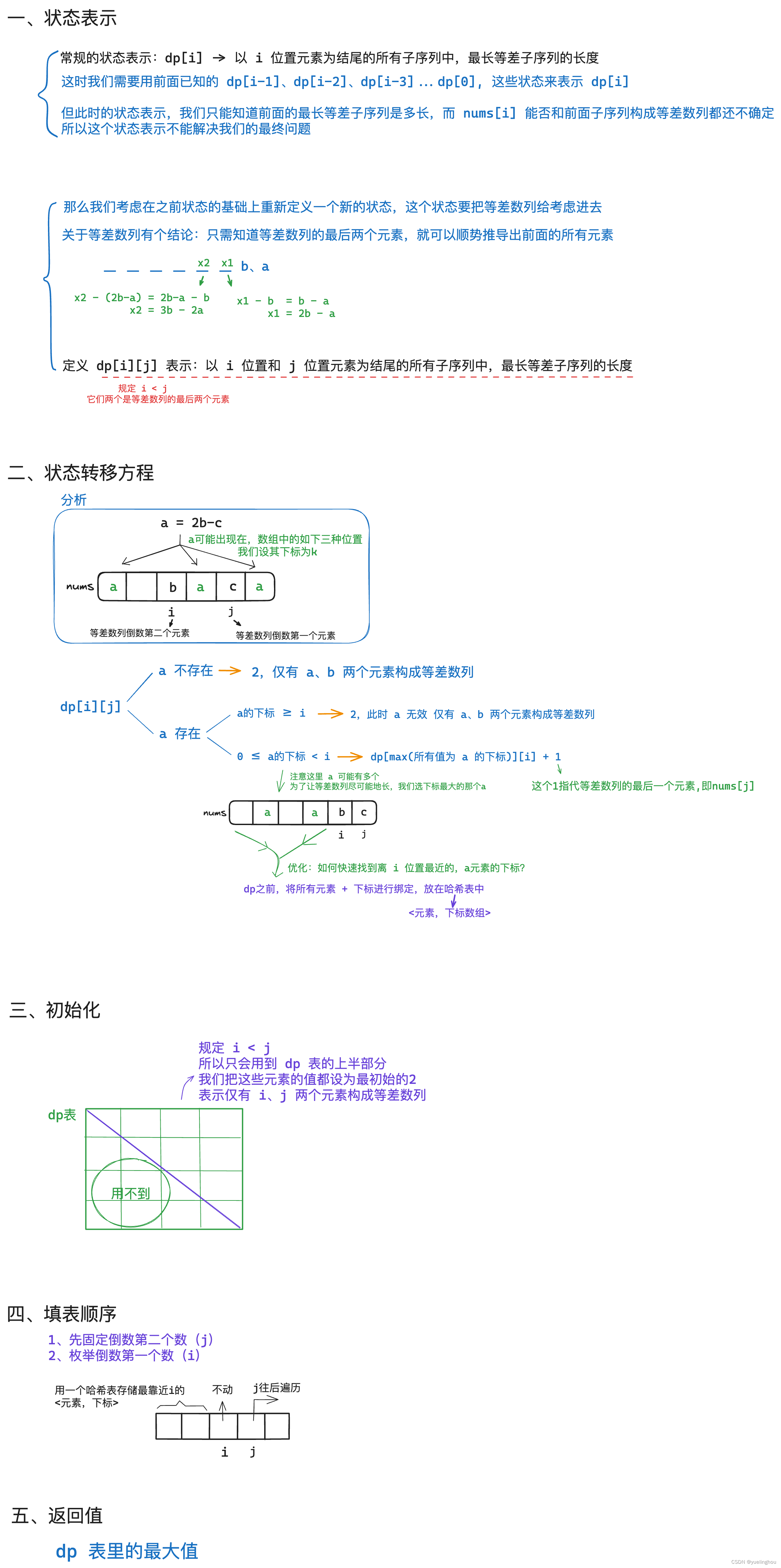
代码编写
class Solution
{
public:
int longestArithSeqLength(vector<int>& nums)
{
// 0、优化
unordered_map<int, int> hash;
hash[nums[0]] = 0;
// 1、建表 && 初始化
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n, 2));
// 2、填表
int ret = 2;
for(int i = 1; i < n - 1; ++i) // 固定倒数第二个数
{
for(int j = i + 1; j < n; ++j) // 枚举倒数第一个数
{
int a = 2 * nums[i] - nums[j];
if(hash.count(a)) dp[i][j] = dp[hash[a]][i] + 1;
ret = max(ret, dp[i][j]);
}
hash[nums[i]] = i; // 更新 nums[i] 的下标
}
// 3、返回值
return ret;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
8. 等差数列划分 II - 子序列

算法原理
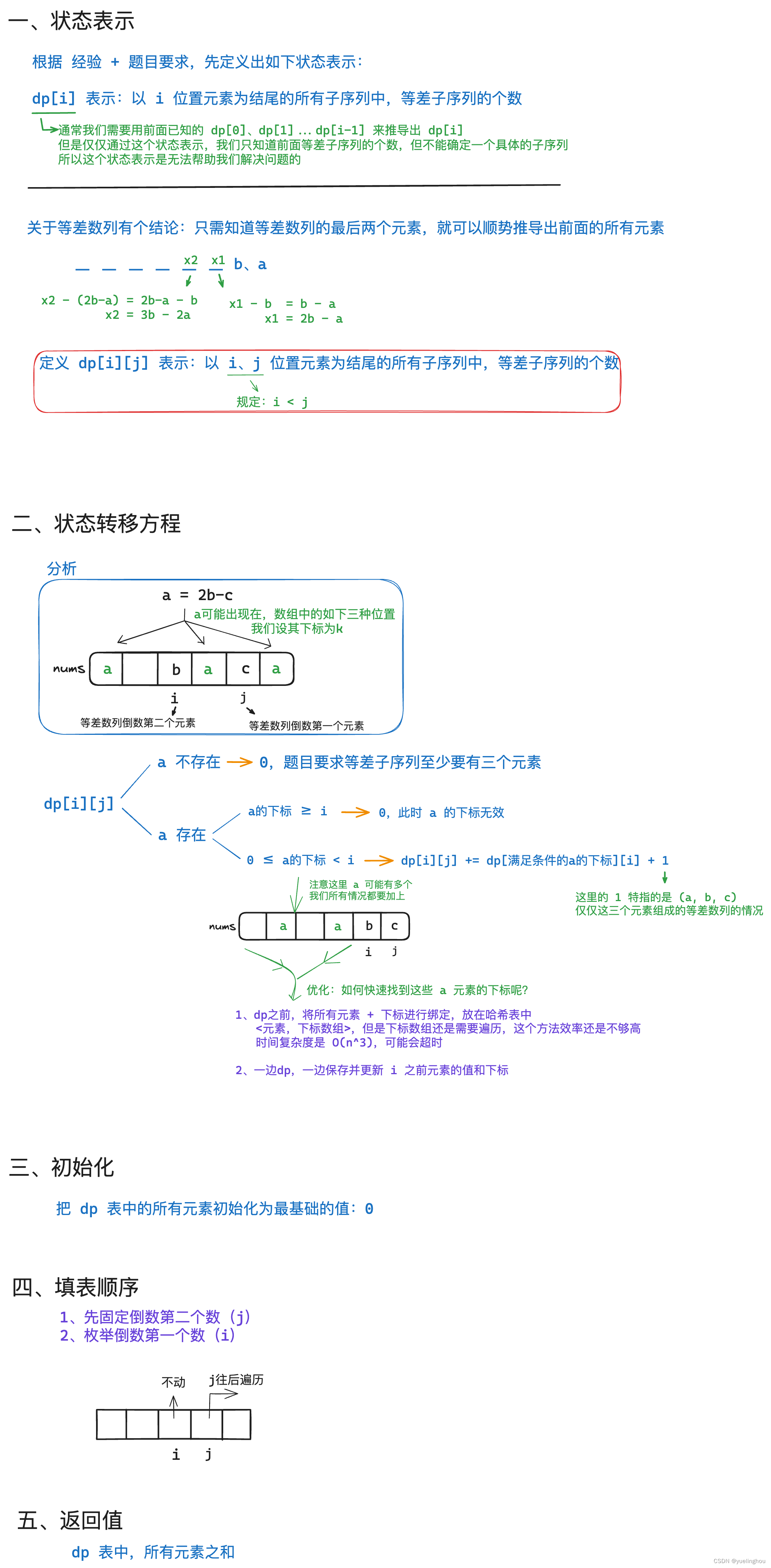
代码编写
class Solution
{
public:
int numberOfArithmeticSlices(vector<int>& nums)
{
// 0、优化
unordered_map<long long, vector<int>> hash;
hash[nums[0]].push_back(0);
// 1、建表 && 初始化
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n));
// 2、填表
int sum = 0; //记录dp表中所有元素之和
for(int i = 1; i < n - 1; ++i)
{
for(int j = i + 1; j < n; ++j)
{
long long a = 2 * (long long)nums[i] - nums[j];
if(hash.count(a))
for(const auto e : hash[a])
dp[i][j] += dp[e][i] + 1;
sum += dp[i][j];
}
hash[nums[i]].push_back(i);
}
// 3、返回值
return sum;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
六. 回文串问题
1. 回文子串

算法原理
-
状态表示:dp[i][j] 表示 s 字符串中,下标范围 [i, j] 的子串,它是否构成回文串

-
状态转移方程

-
初始化:创建一个 n*n 的 dp 表即可,存储元素全是 bool 类型的 false
-
填表顺序:从下往上填写每一行,每一行再从左往右填写
-
返回值: dp 表里面 true 的个数
代码编写
class Solution
{
public:
int countSubstrings(string s)
{
int count = 0;
size_t n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
for (int i = n - 1; i >= 0; --i)
for (int j = i; j < n; ++j)
if (s[i] == s[j] && (i == j || i + 1 == j || dp[i + 1][j - 1]))
dp[i][j] = true, ++count;
return count;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
2. 最长回文子串

算法原理

代码编写
class Solution
{
public:
string longestPalindrome(string s)
{
// 1、建表
size_t n = s.size();
// 用来存储最长子串的起始下标和长度,到最后可以使用 substr 还原出该子串
pair<size_t, size_t> pr(n - 1, 1);
// dp 表用来存储所有字串的回文情况
vector<vector<bool>> dp(n, vector<bool>(n));
// 2、填表
for(int i = n - 1; i >= 0; --i)
{
for(int j = i; j < n; ++j)
{
if(s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if(dp[i][j] && j - i + 1 > pr.second)
pr.first = i, pr.second = j - i + 1;
}
}
// 3、返回值
return s.substr(pr.first, pr.second);
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
3. 分割回文串 IV

算法原理

代码编写
class Solution
{
public:
bool checkPartitioning(string s)
{
// 1、用 dp 把所有字串是否是回文预处理一下
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
for(int i = n - 1; i >= 0; --i)
for(int j = i; j < n; ++j)
if(s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
// 2、枚举所有第二个字符串的起始位置和结束位置
for(int i = 1; i < n - 1; ++i)
for(int j = i; j < n - 1; ++j)
if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])
return true;
return false;
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
4. 分割回文串 II

算法原理
-
状态表示:dp[i] 表示: [0, i] 区间的子字符串,最少的分割次数
-
状态转移方程
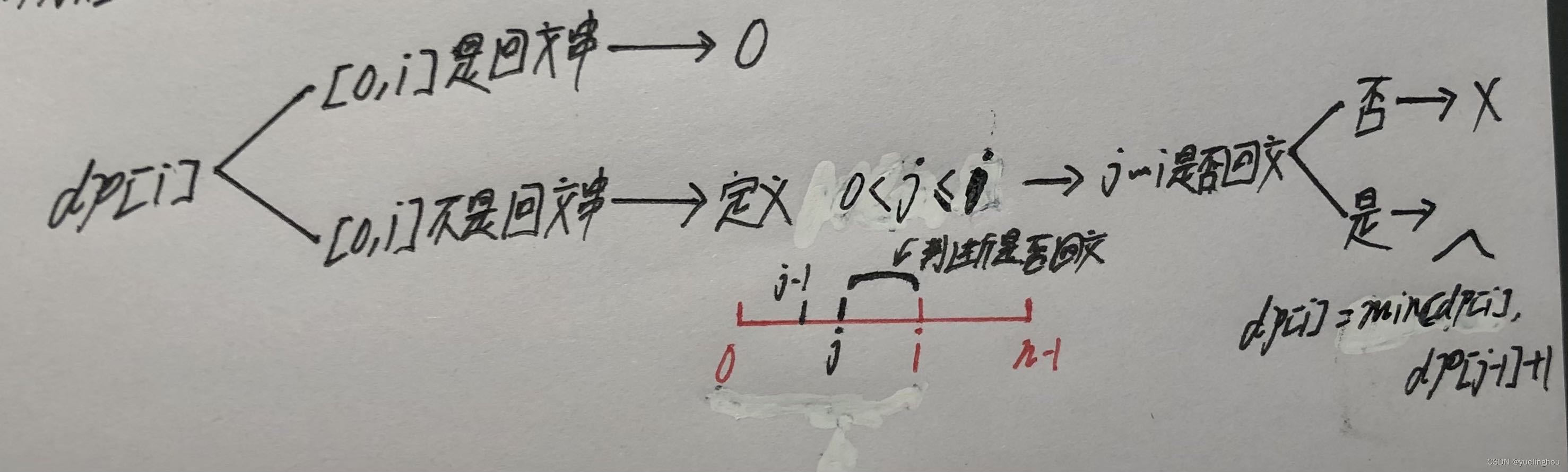
-
初始化:在更新 dp[i] 时,需要比较原 dp[i] 和 dp[j - 1] + 1,二者的最小值。我们把 dp 表中的元素一开始都初始化为 INT_MAX,主要是为了防止第一次更新 dp[i] 时,不让初始的 dp[i] 去影响我们的更新结果。
-
填表顺序:从左往右
-
返回值:dp[n - 1]
代码编写
class Solution
{
public:
int minCut(string s)
{
// 1、在 isPal 表中统计所有字串的回文信息
int n = s.size();
vector<vector<bool>> isPal(n, vector<bool>(n));
for(int i = n - 1; i >= 0; --i)
for(int j = i; j < n; ++j)
if(s[i] == s[j])
isPal[i][j] = !(i + 1 < j) || isPal[i + 1][j - 1];
// 2、创建并填写 dp 表
vector<int> dp(n, INT_MAX);
for(int i = 0; i < n; ++i)
{
if(isPal[0][i])
{
dp[i] = 0;
}
else
{
for(int j = 1; j <= i; ++j)
{
if(isPal[j][i]) dp[i] = min(dp[i], dp[j-1] + 1);
}
}
}
// 3、返回值
return dp[n - 1];
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
5. 最长回文子序列

算法原理
- 状态表示

- 状态转移方程

- 初始化

- 填表顺序:从上往下填每一行,每一行再从左往右填写
- 返回值:dp[0][n - 1]
代码编写
class Solution
{
public:
int longestPalindromeSubseq(string s)
{
// 1、建表
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
// 2、填表
for(int i = n - 1; i >= 0; --i)
for(int j = i; j < n; ++j)
{
if(s[i] == s[j])
dp[i][j] = i + 1 >= j ? (j - i + 1) : dp[i + 1][j - 1] + 2;
else
dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
}
// 3、返回值
return dp[0][n - 1];
}
};
6. 让字符串成为回文串的最少插入次数

算法原理
- 状态表示

- 状态转移方程
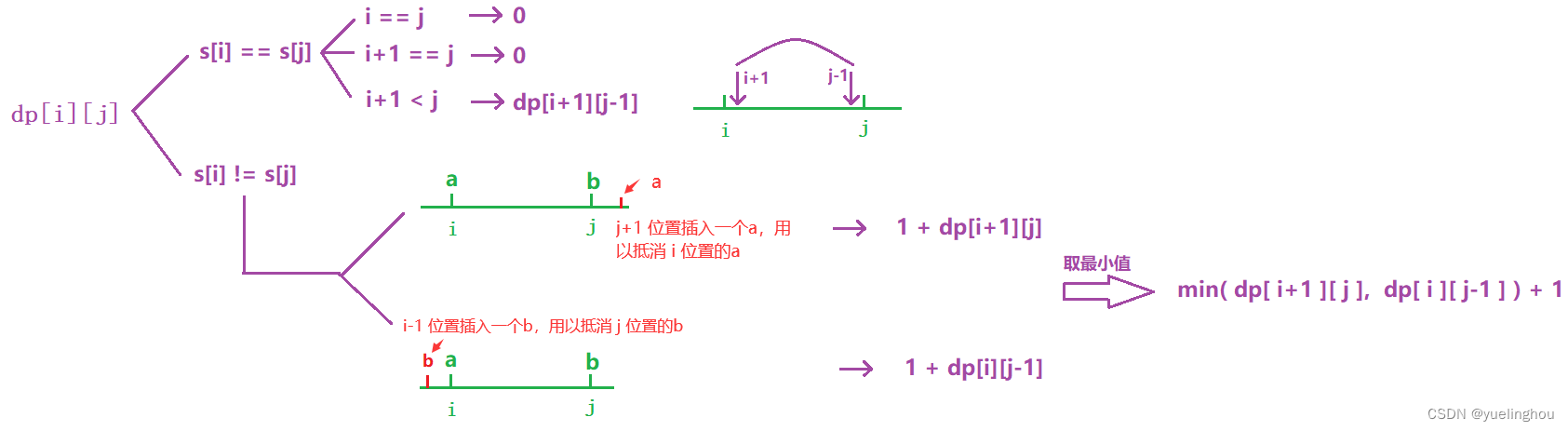
- 初始化
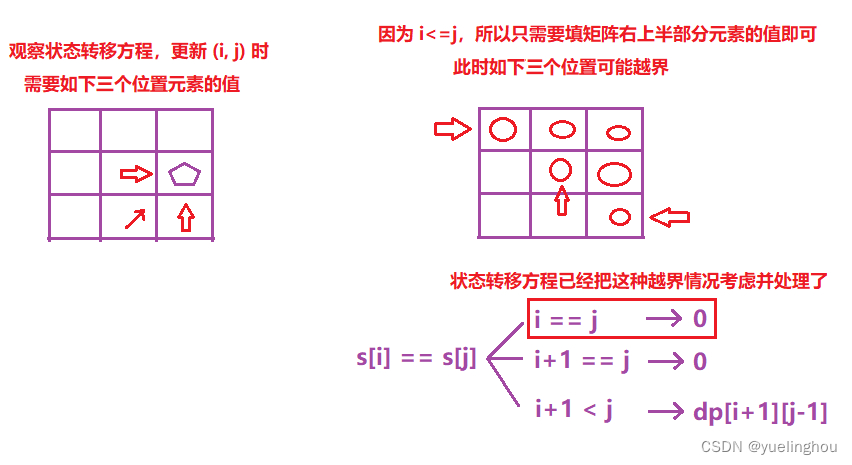
- 填表顺序

- 返回值:dp[0][n-1]
代码编写
class Solution
{
public:
int minInsertions(string s)
{
// 1、建表
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
// 2、填表
for(int i = n - 1; i >= 0; --i)
for(int j = i + 1; j < n; ++j)
if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1];
else dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1;
// 3、返回值
return dp[0][n-1];
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
七. 双数组 dp 问题
1. 最长公共子序列

算法原理
-
状态表示

-
状态转移方程
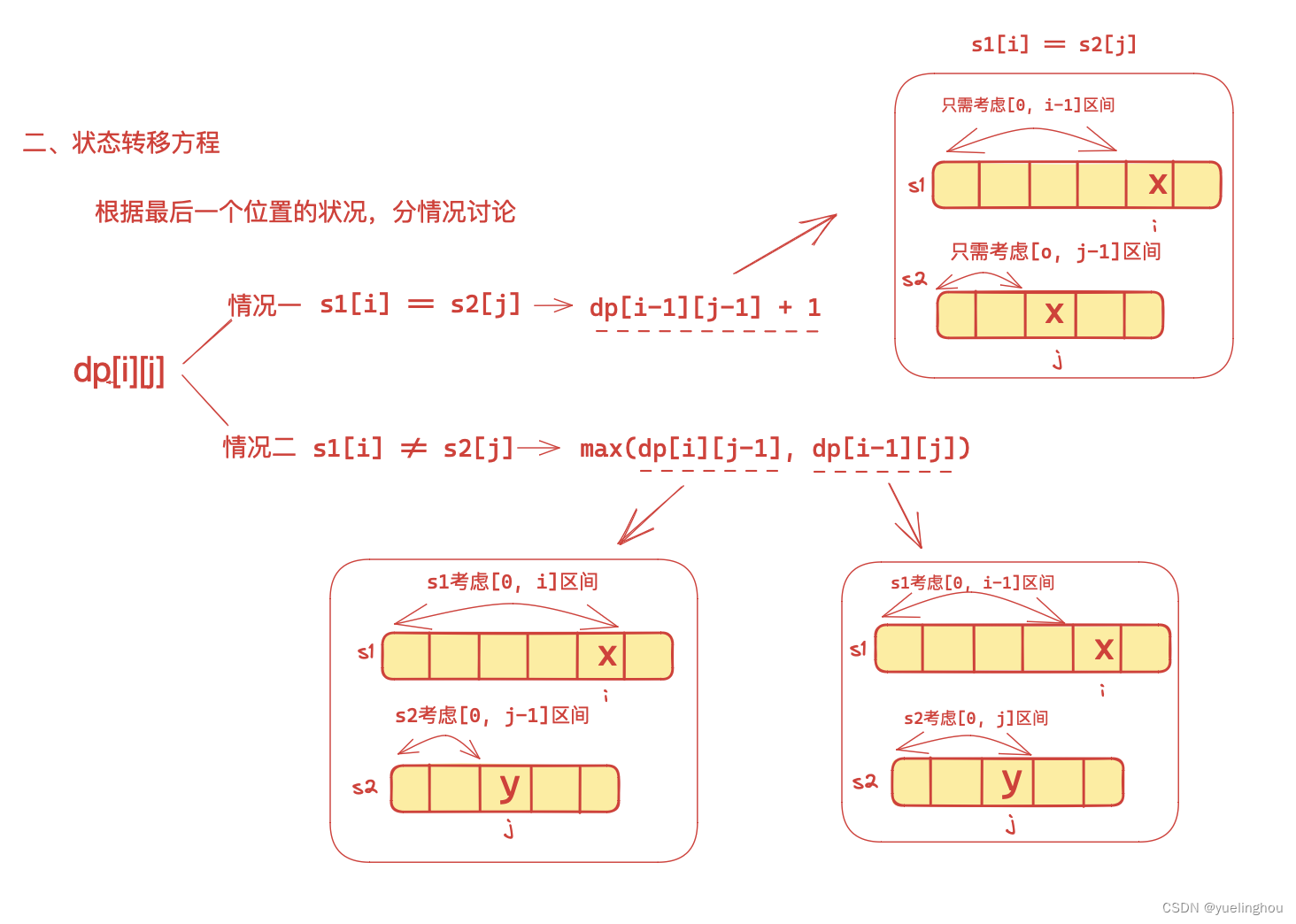
-
初始化
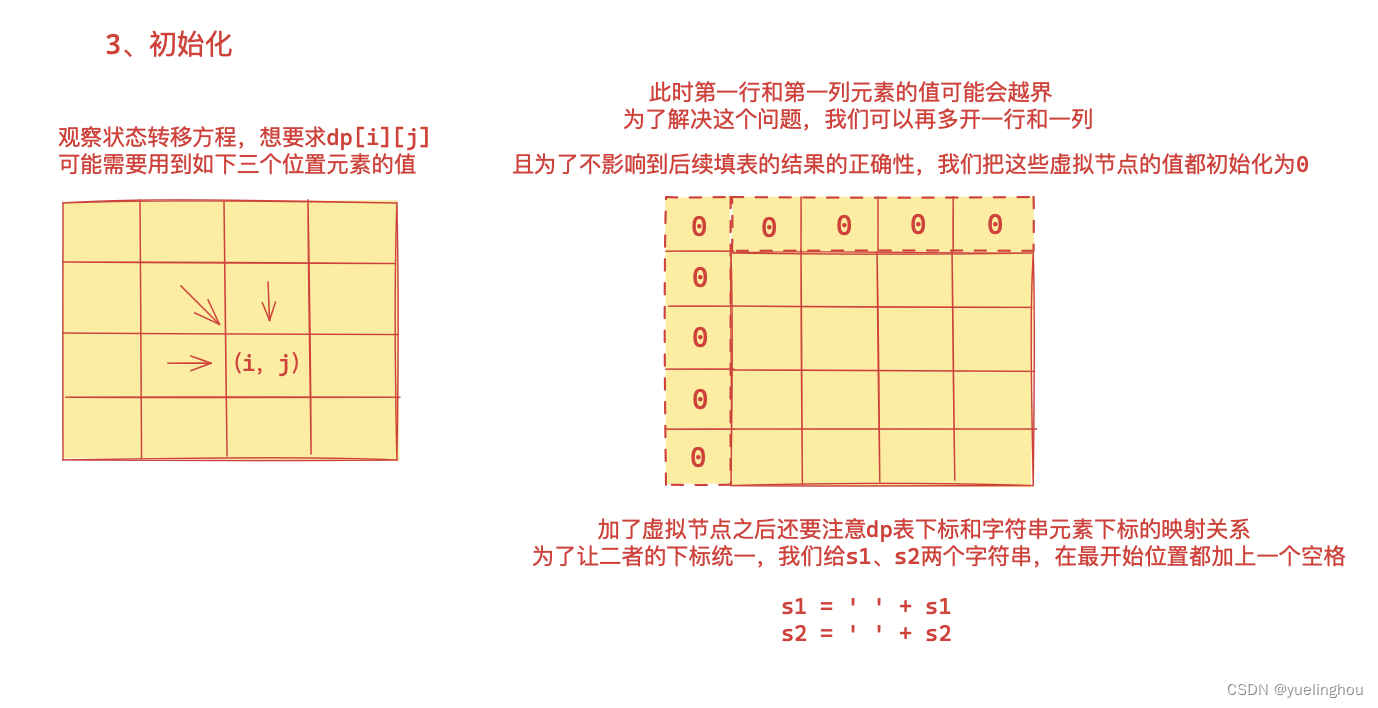
-
填表顺序

-
返回值
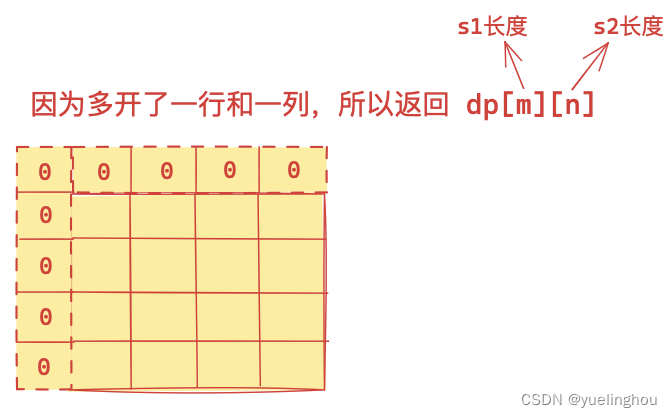
代码编写
class Solution
{
public:
int longestCommonSubsequence(string s1, string s2)
{
// 1、建表
int m = s1.size(), n = s2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 2、初始化
s1 = ' ' + s1;
s2 = ' ' + s2;
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
if(s1[i] == s2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
// 3、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
2. 不相交的线

算法原理
-
状态表示

-
状态转移方程

-
初始化
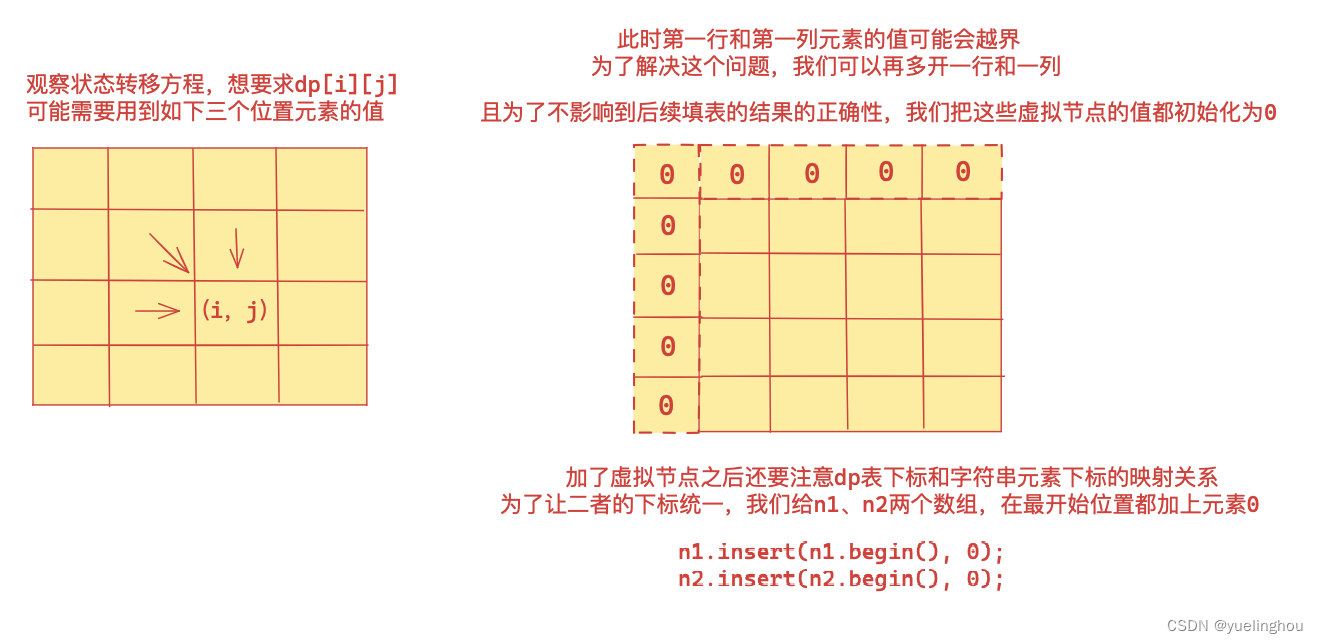
-
填表顺序

-
返回值
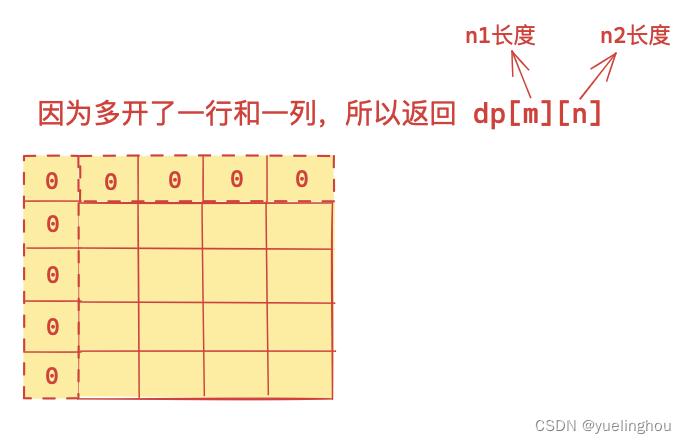
代码编写
class Solution
{
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2)
{
// 1、建表
int m = nums1.size(), n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 2、初始化
nums1.insert(nums1.begin(), 0);
nums2.insert(nums2.begin(), 0);
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
if(nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/
3. 不同的子序列

算法原理
-
状态表示

-
状态转移方程

-
初始化

-
填表顺序

-
返回值:dp[m][n],其中 m 为 t 字符串的长度,n 为 s 字符串的长度
代码编写
class Solution
{
public:
int numDistinct(string s, string t)
{
// 1、建表
int m = t.size(), n = s.size();
vector<vector<long long>> dp(m + 1, vector<long long>(n + 1));
// 2、初始化
s = ' ' + s;
t = ' ' + t;
for(int j = 0; j <= n; ++j) dp[0][j] = 1;
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
if(t[i] == s[j])
dp[i][j] = (dp[i][j - 1] + dp[i - 1][j - 1]) % (10000000000 + 7);
else
dp[i][j] = dp[i][j - 1] % (10000000000 + 7);
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
4. 通配符匹配

算法原理
-
状态表示

-
状态转移方程
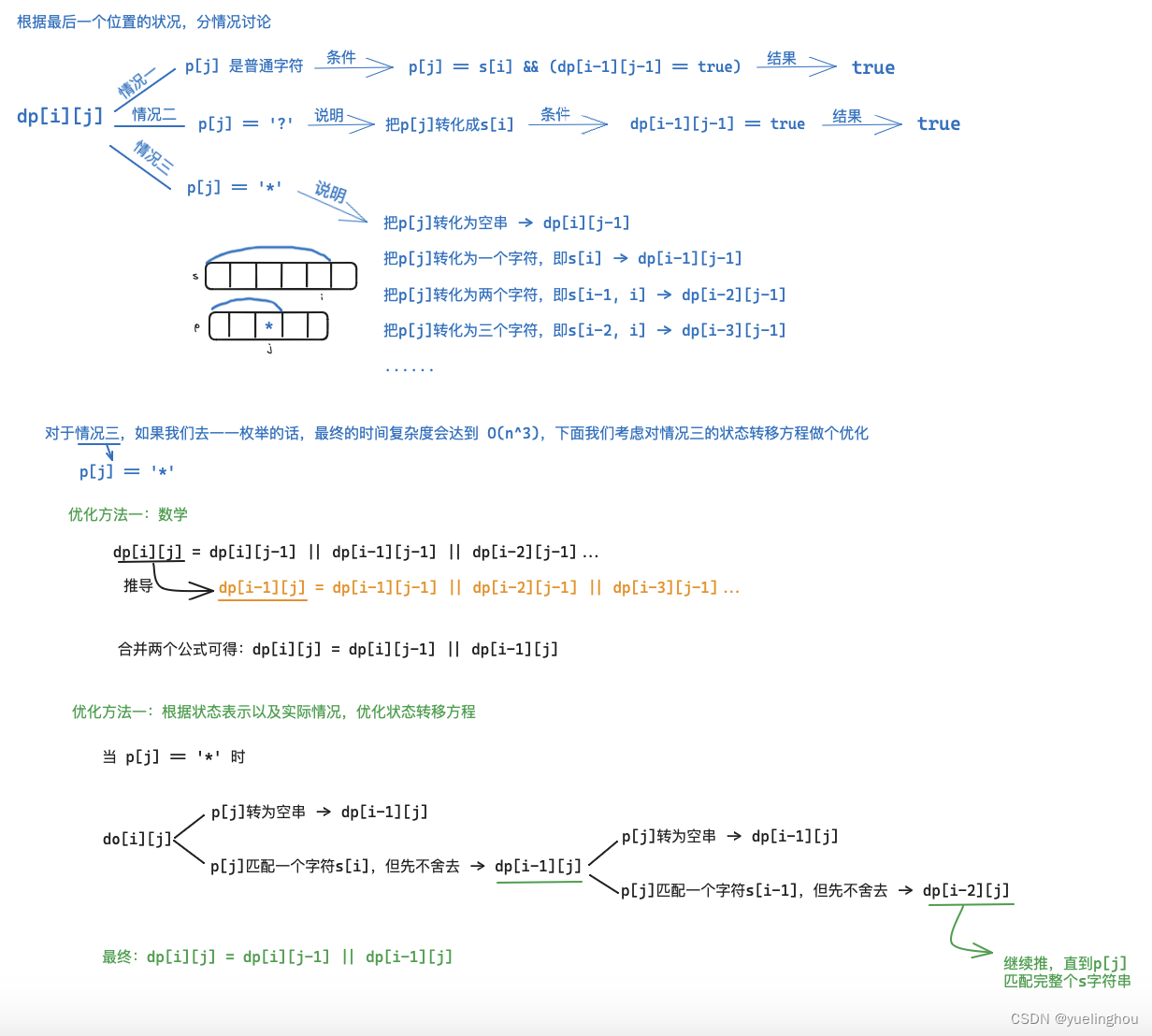
-
初始化
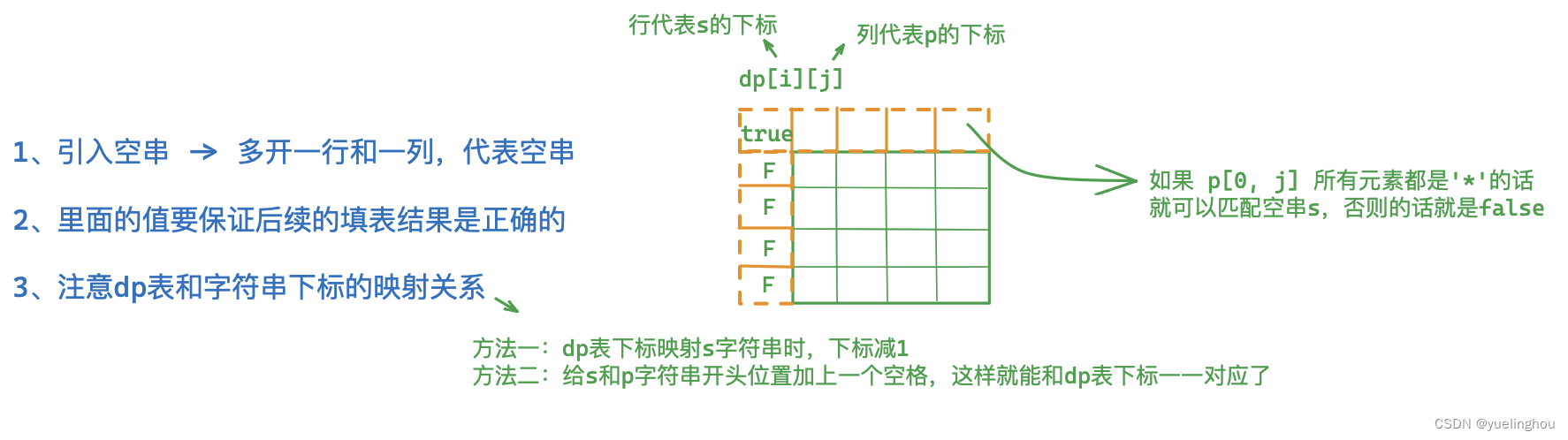
-
填表顺序

-
返回值:dp[m][n],其中m为字符串s的长度,n为字符串p的长度
代码编写
class Solution
{
public:
bool isMatch(string s, string p)
{
// 1、建表
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
// 2、初始化
s = ' ' + s;
p = ' ' + p;
for(int j = 0; j <= n; ++j)
{
if(j == 0)
dp[0][j] = true;
else
if(p[j] == '*' && dp[0][j - 1] == true) dp[0][j] = true;
}
// 3、填表
for(int i = 1; i <= m; ++i)
{
for(int j = 1; j <= n; ++j)
{
if(p[j] == '*') // p[j] == '*'
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
else // p[j] == '?' 或 普通字符
if((p[j] == '?' || s[i] == p[j]) && dp[i - 1][j - 1])
dp[i][j] = true;
}
}
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
5. 正则表达式匹配

算法原理
-
状态表示

-
状态转移方程
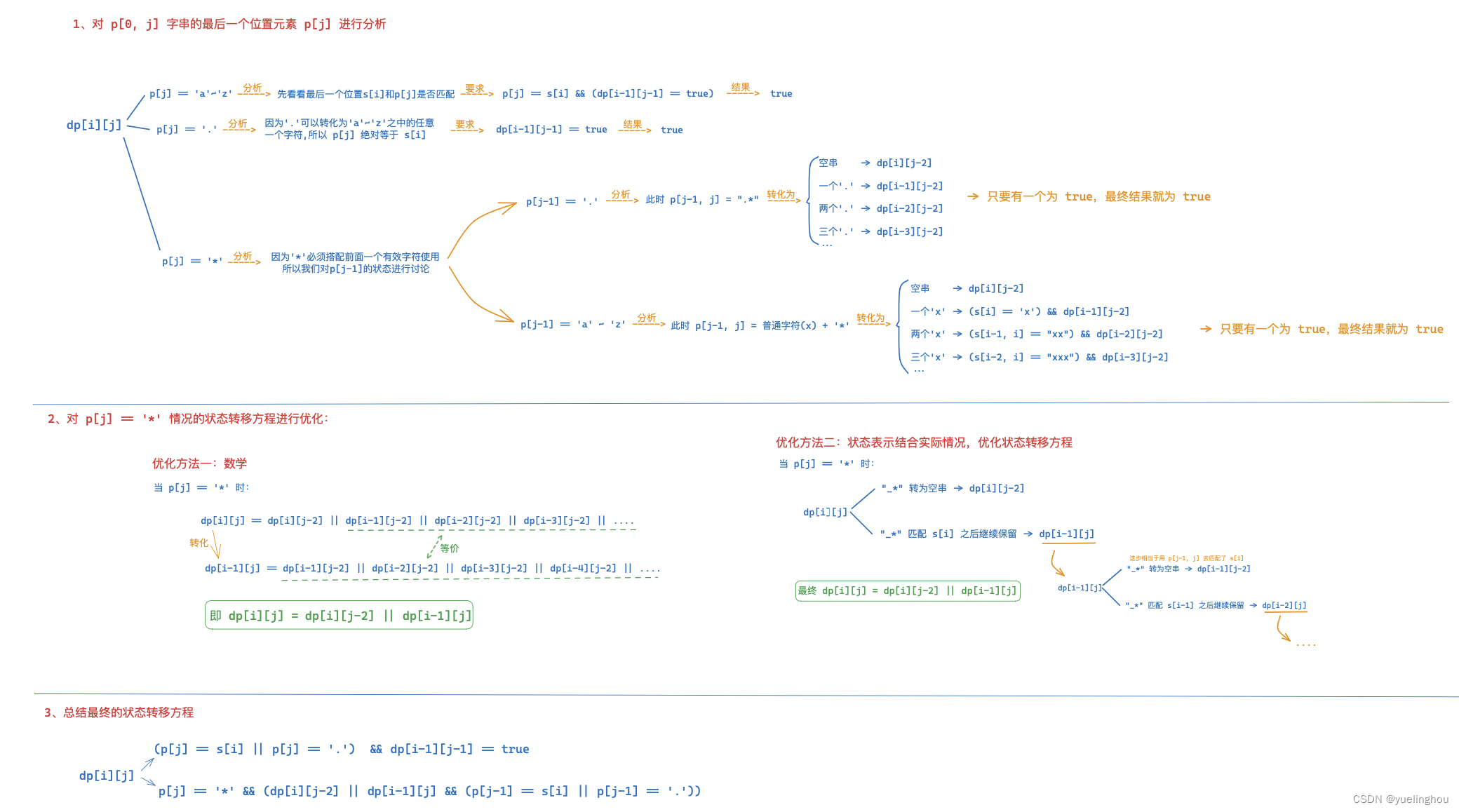
-
初始化

-
填表顺序
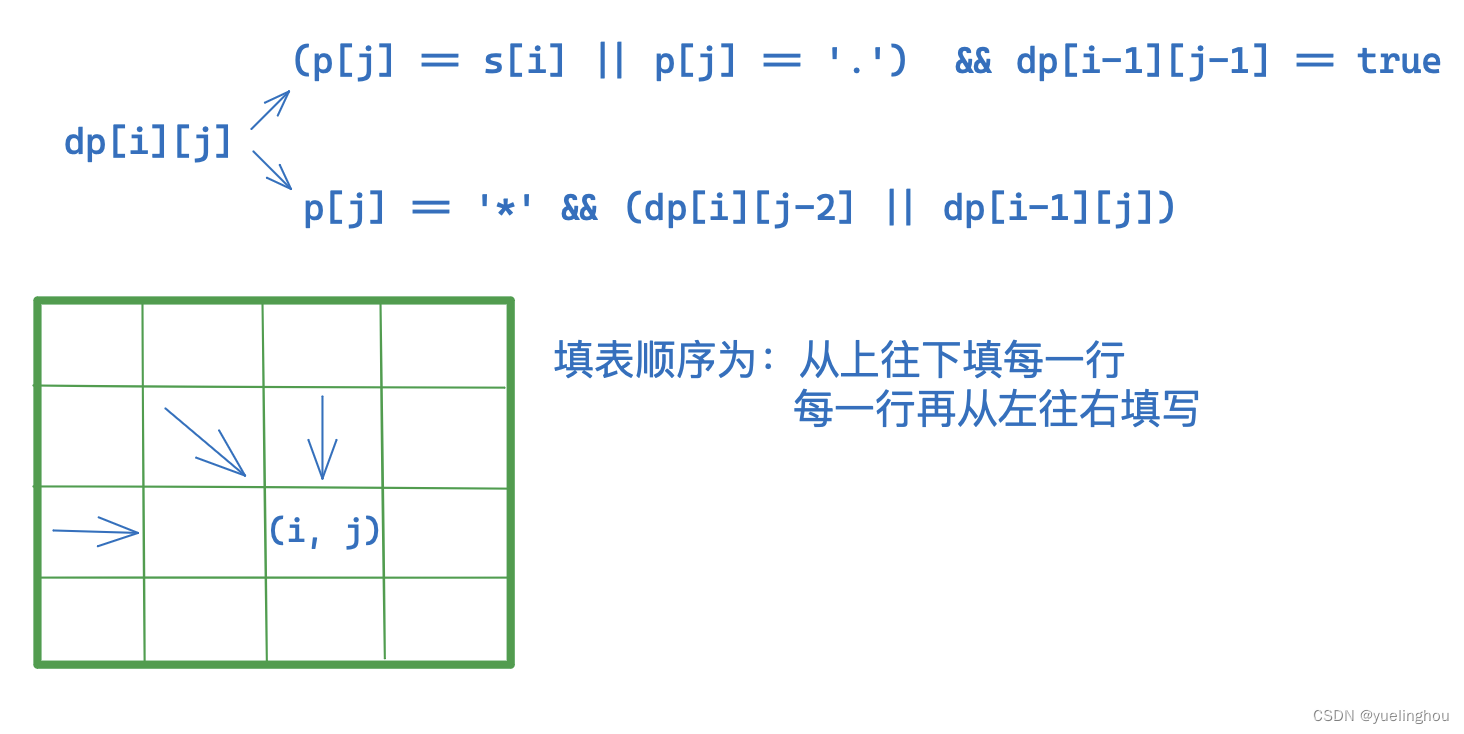
-
返回值:dp[m][n],m为s字符串的长度,n为p字符串的长度
代码编写
class Solution
{
public:
bool isMatch(string s, string p)
{
// 1、建表
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
// 2、初始化
s = ' ' + s;
p = ' ' + p;
dp[0][0] = true;
for(int j = 2; j <= n; j += 2)
if(p[j] == '*') dp[0][j] = true;
else break;
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
if(p[j] == '*')
dp[i][j] = dp[i][j-2] || (p[j-1] == s[i] || p[j-1] == '.') && dp[i-1][j];
else
dp[i][j] = (p[j] == s[i] || p[j] == '.') && dp[i-1][j-1];
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
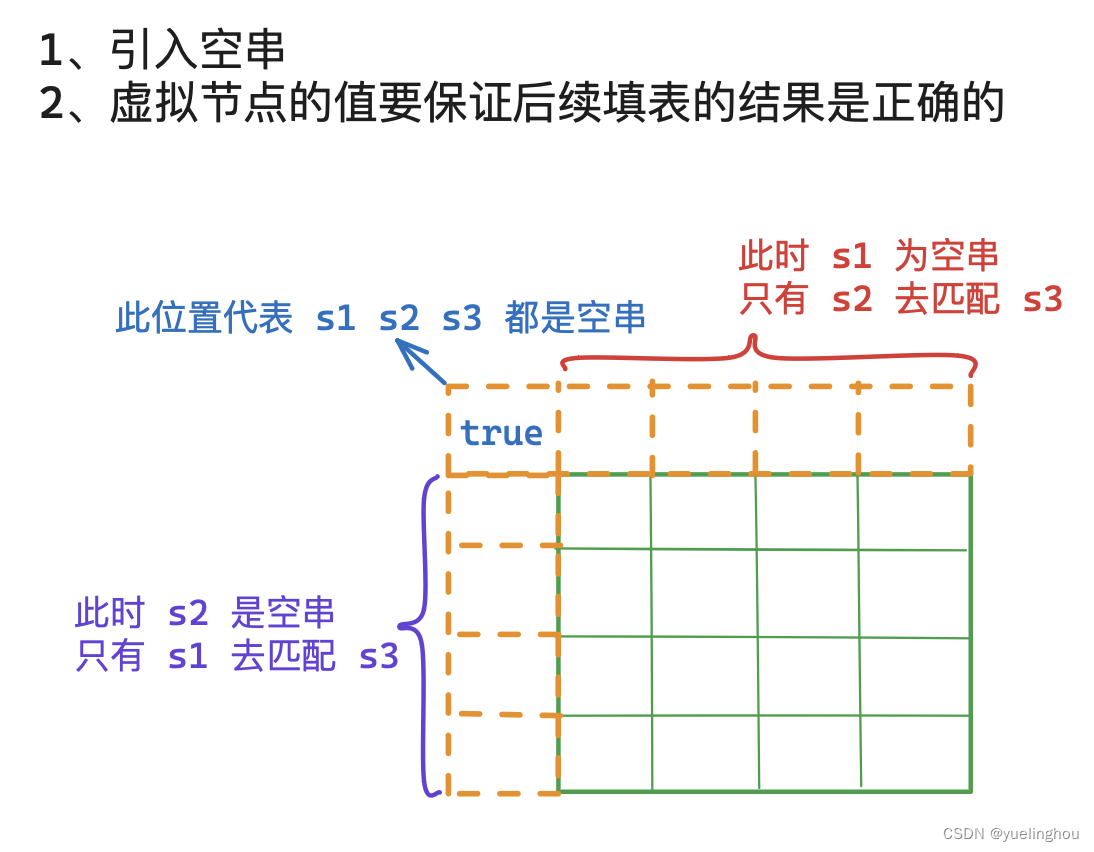
6. 交错字符串
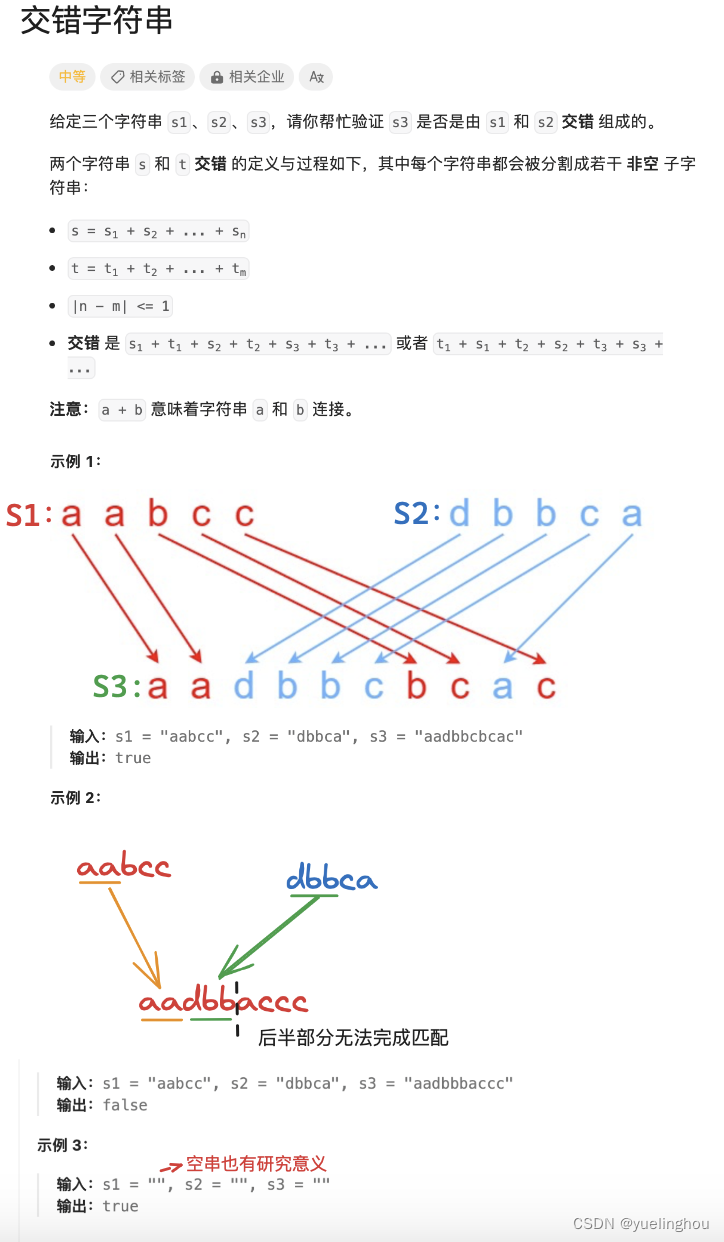
算法原理
-
预处理
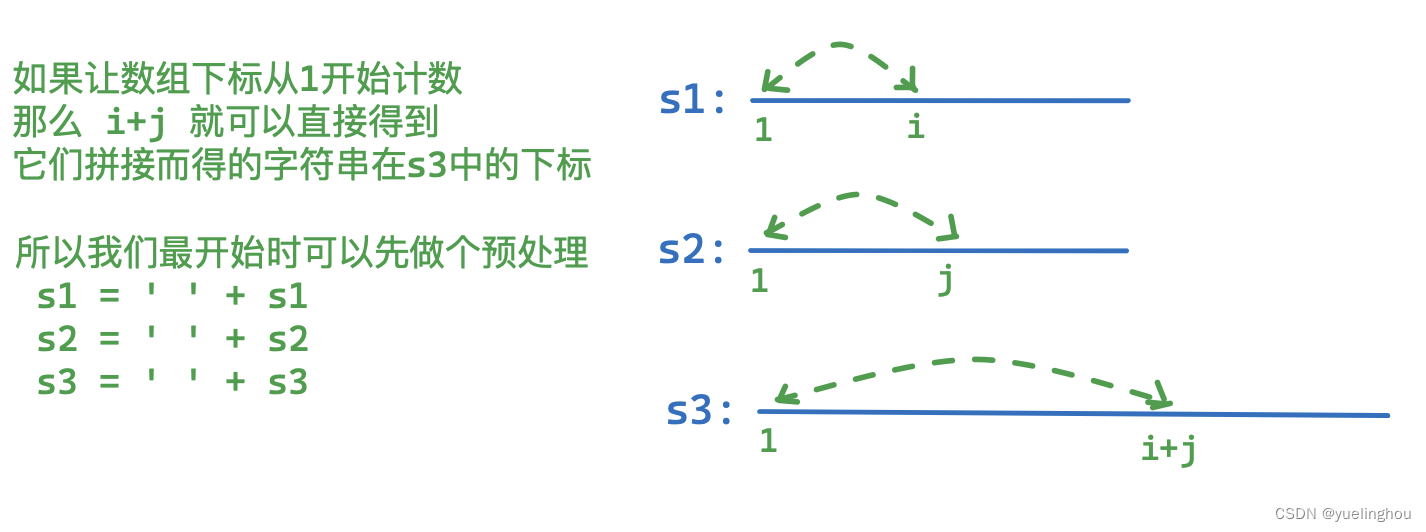
-
状态表示
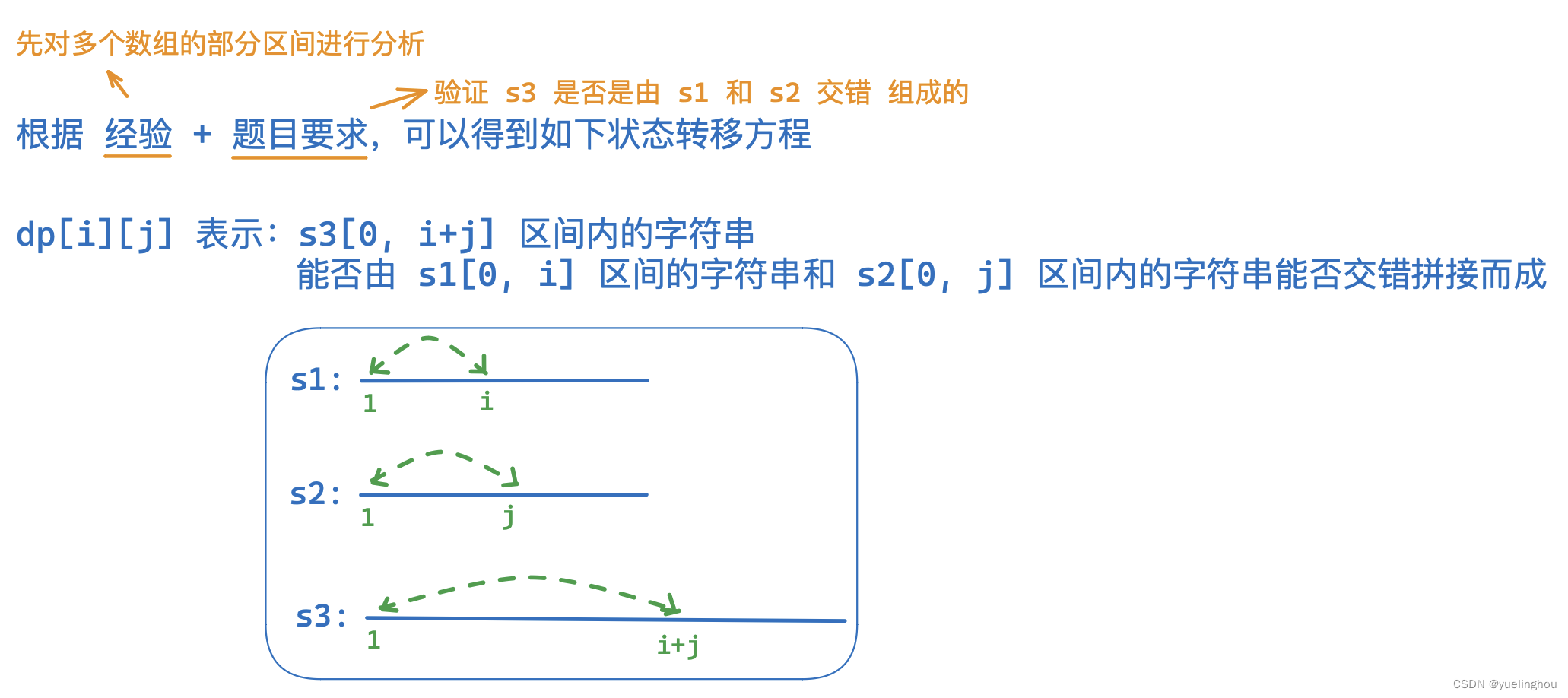
-
状态转移方程

-
初始化
-
填表顺序

-
返回值:dp[m][n],其中 m 为 s1 的长度,n 为 s2 的长度
代码编写
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
// 1、建表
int m = s1.size(), n = s2.size();
if(m + n != s3.size()) return false;
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
// 2、初始化
s1 = ' ' + s1;
s2 = ' ' + s2;
s3 = ' ' + s3;
dp[0][0] = true;
for(int i = 1; i <= m; ++i) // 初始化第一行
if(s1[i] == s3[i]) dp[i][0] = true;
else break;
for(int j = 1; j <= n; ++j) // 初始化第一列
if(s2[j] == s3[j]) dp[0][j] = true;
else break;
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
dp[i][j] = (s1[i] == s3[i+j] && dp[i-1][j])
||(s2[j] == s3[i+j] && dp[i][j-1]);
// 4、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
7. 两个字符串的最小ASCII删除和

算法原理
-
分析:题目要求我们计算让两个子序列相同时,所需删除字符的 ASCll 最小和既然要删除的字符之和最小,那么留下的子序列之和就是最大,所以可以使用“正难则反”的思想,去计算两个字符串中所有公共子序列里面,ASCll 值最大的公共子序列是那个。
-
状态表示

-
状态转移方程

-
初始化
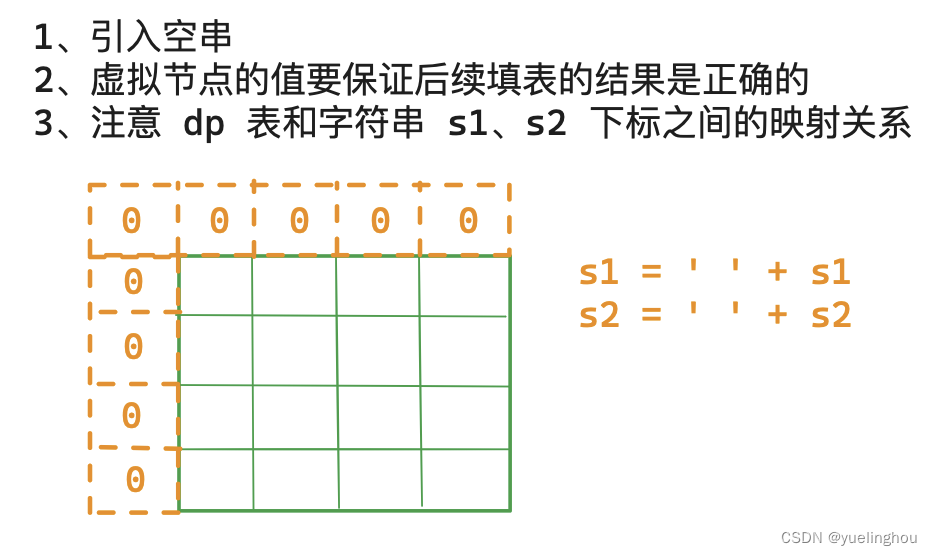
-
填表顺序

-
返回值

代码编写
class Solution
{
public:
int minimumDeleteSum(string s1, string s2)
{
// 1、建表
int m = s1.size(), n = s2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 2、初始化
s1 = ' ' + s1;
s2 = ' ' + s2;
// 3、填表
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
{
int x1 = (s1[i] == s2[j] ? dp[i-1][j-1] + s1[i] : 0);
int x2 = dp[i][j - 1];
int x3 = dp[i - 1][j];
dp[i][j] = max(max(x2, x3), x1);
}
// 4、返回值
int sum = 0;
// 计算总和时不要把两个字符串最开头的空格给算进去
for(int i = 1; i <= m; ++i) sum += s1[i];
for(int j = 1; j <= n; ++j) sum += s2[j];
return sum - 2 * dp[m][n];
}
};
/*
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
*/
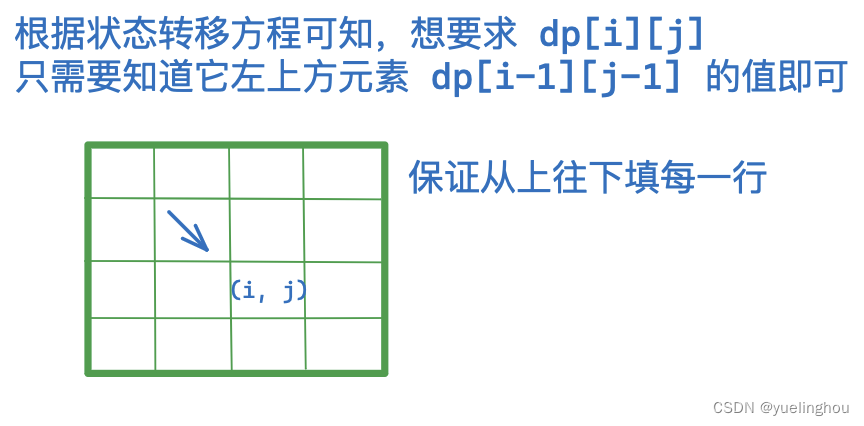
8. 最长重复子数组

算法原理
-
状态表示

-
状态转移方程

-
初始化
-
填表顺序
-
返回值:dp 表中的最大值
八. 背包问题
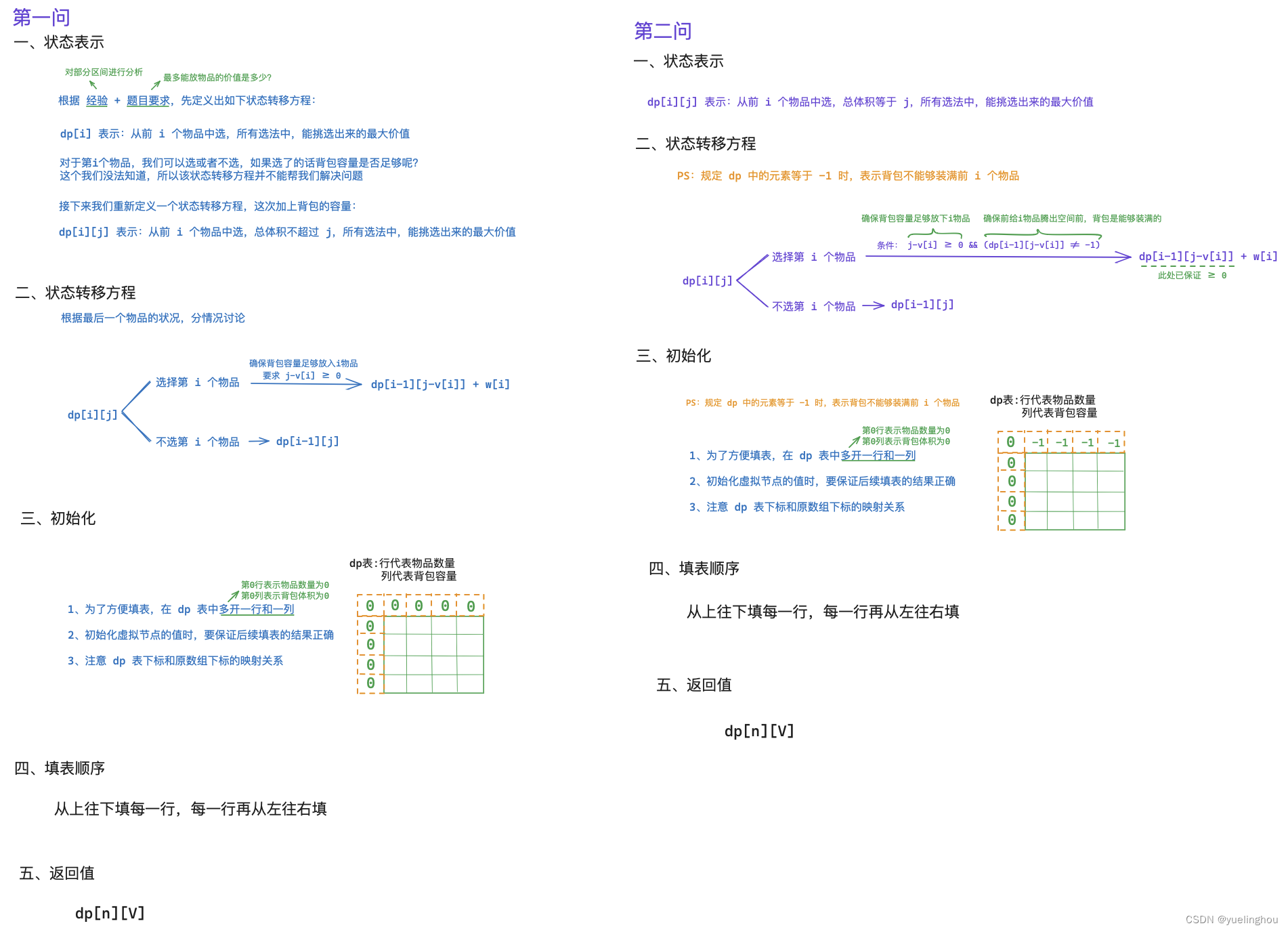
1.【扫盲】什么是背包问题?

2.【模板】01背包

题目解析

算法原理
代码编写
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main()
{
// 1、数据输入
int n = 0; // 物品个数
int V = 0; // 背包容量
cin >> n >> V;
// n 个物品的体积和价值表,其中第0个位置表示一个虚拟物品
// 它的体积和价值都为0,设置它的目的是为了下标和dp表对应
vector<int> v(n + 1), w(n + 1);
for(int i = 1; i <= n; ++i)
cin >> v[i] >> w[i];
// 2、创建 dp 表
vector<vector<int>> dp(n + 1, vector<int>(V + 1));
// 3、解决第一问
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j - v[i] >= 0) dp[i][j] = max(dp[i][j], w[i] + dp[i - 1][j - v[i]]);
}
cout << dp[n][V] << endl;
// 4、解决第二问
for(int j = 1; j <= V; ++j) dp[0][j] = -1;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j - v[i] >= 0 && dp[i - 1][j - v[i]] != -1) dp[i][j] = max(dp[i][j], w[i] + dp[i - 1][j - v[i]]);
}
cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
return 0;
}
/*
- 时间复杂度:O(nV)
- 空间复杂度:O(nV)
*/
优化
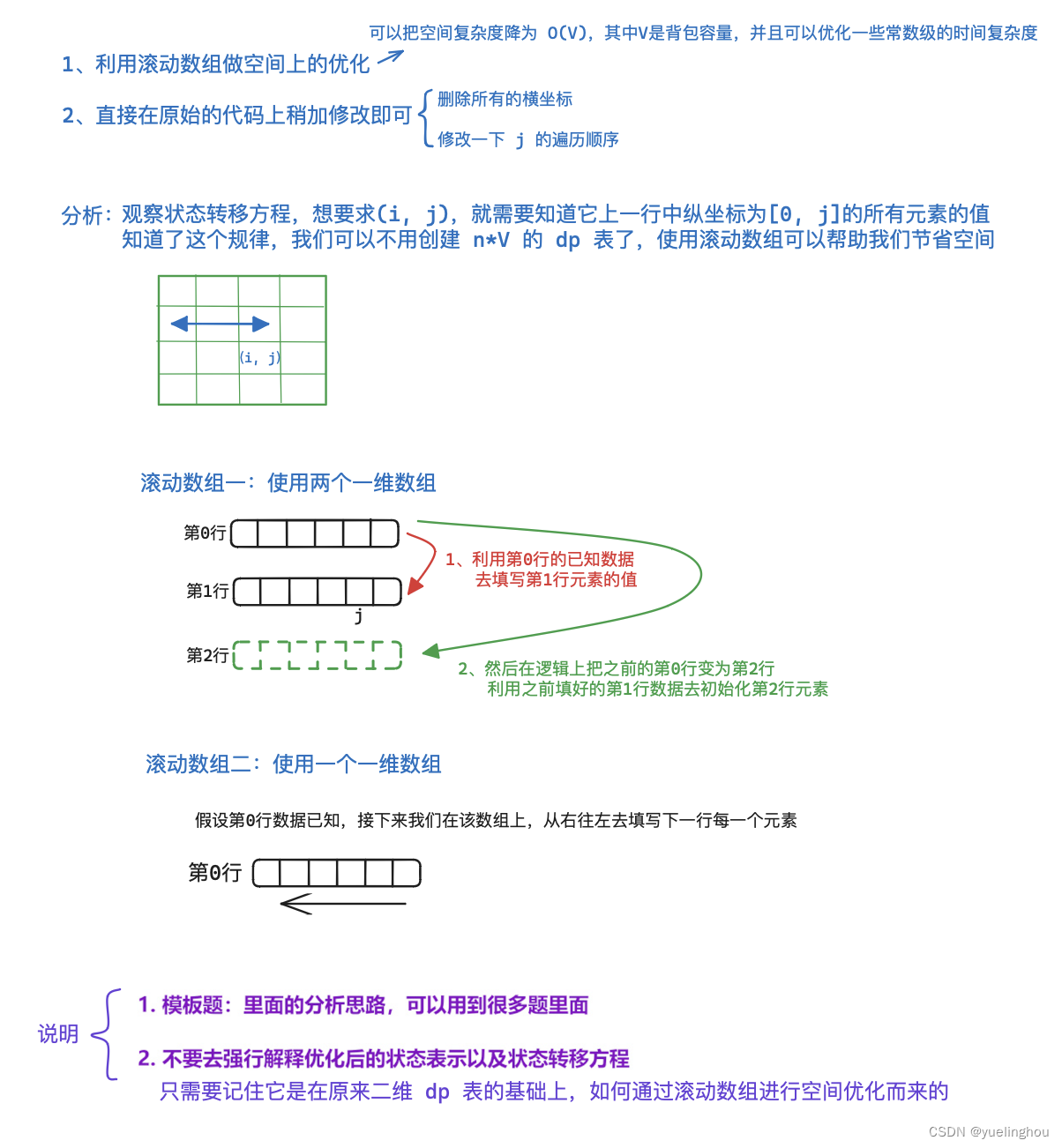
优化后代码如下:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main()
{
// 1、数据输入
int n = 0; // 物品个数
int V = 0; // 背包容量
cin >> n >> V;
// n 个物品的体积和价值表,其中第0个位置表示一个虚拟物品
// 它的体积和价值都为0,设置它的目的是为了下标和dp表对应
vector<int> v(n + 1), w(n + 1);
for(int i = 1; i <= n; ++i)
cin >> v[i] >> w[i];
// 2、创建 dp 表
vector<int> dp(V + 1);
// 3、解决第一问
for(int i = 1; i <= n; ++i)
for(int j = V; j - v[i] >= 0; --j)
dp[j] = max(dp[j], w[i] + dp[j - v[i]]);
cout << dp[V] << endl;
// 4、解决第二问
for(int j = 1; j <= V; ++j) dp[j] = -1;
for(int i = 1; i <= n; ++i)
for(int j = V; j - v[i] >= 0; --j)
{
if(dp[j - v[i]] != -1) dp[j] = max(dp[j], w[i] + dp[j - v[i]]);
}
cout << (dp[V] == -1 ? 0 : dp[V]) << endl;
return 0;
}
/*
- 时间复杂度:O(nV)
- 空间复杂度:O(V)
*/
分割等和子集

算法原理
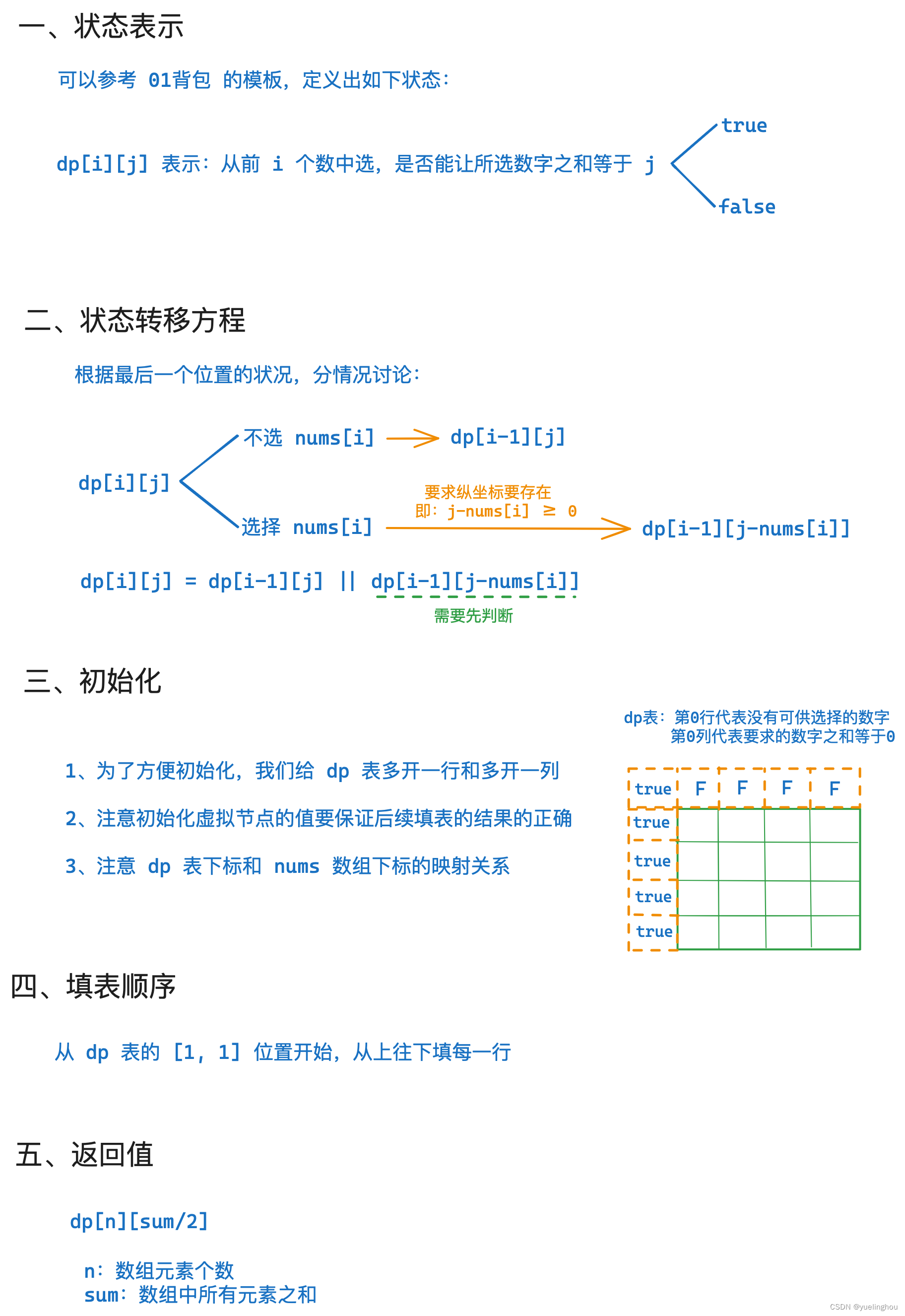
代码编写
class Solution
{
public:
bool canPartition(vector<int>& nums)
{
// 1、建表
int n = nums.size(), sum = 0;
for(const auto e : nums) sum += e; // 计算所有数字之和
if(sum % 2) return false; // 如果数组之和为奇数,则不可能分割成两个等和子集
vector<vector<bool>> dp(n + 1, vector<bool>(sum/2 + 1)); // 创建 dp 表
// 2、初始化
for(int i = 0; i <= n; ++i) dp[i][0] = true;
// 3、填表(注意 dp 表下标和 nums 表下标的映射关系)
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= sum/2; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j - nums[i - 1] >= 0) dp[i][j] = dp[i][j] || dp[i-1][j - nums[i - 1]];
}
// 4、返回值
return dp[n][sum/2];
}
};
/*
- 时间复杂度:O(n*sum)
- 空间复杂度:O(n*sum)
*/
// 空间优化版本
// 1. 删除横坐标
// 2. 修改纵坐标遍历顺序
class Solution
{
public:
bool canPartition(vector<int>& nums)
{
// 1、建表
int n = nums.size(), sum = 0;
for(const auto e : nums) sum += e; // 计算所有数字之和
if(sum % 2) return false; // 如果数组之和为奇数,则不可能分割成两个等和子集
vector<bool> dp(sum/2 + 1); // 创建 dp 表
// 2、初始化
dp[0] = true;
// 3、填表(注意 dp 表下标和 nums 表下标的映射关系)
for(int i = 1; i <= n; ++i)
for(int j = sum/2; j >= nums[i - 1]; --j)
dp[j] = dp[j] || dp[j - nums[i - 1]];
// 4、返回值
return dp[sum/2];
}
};
/*
- 时间复杂度:O(n*sum)
- 空间复杂度:O(sum)
*/
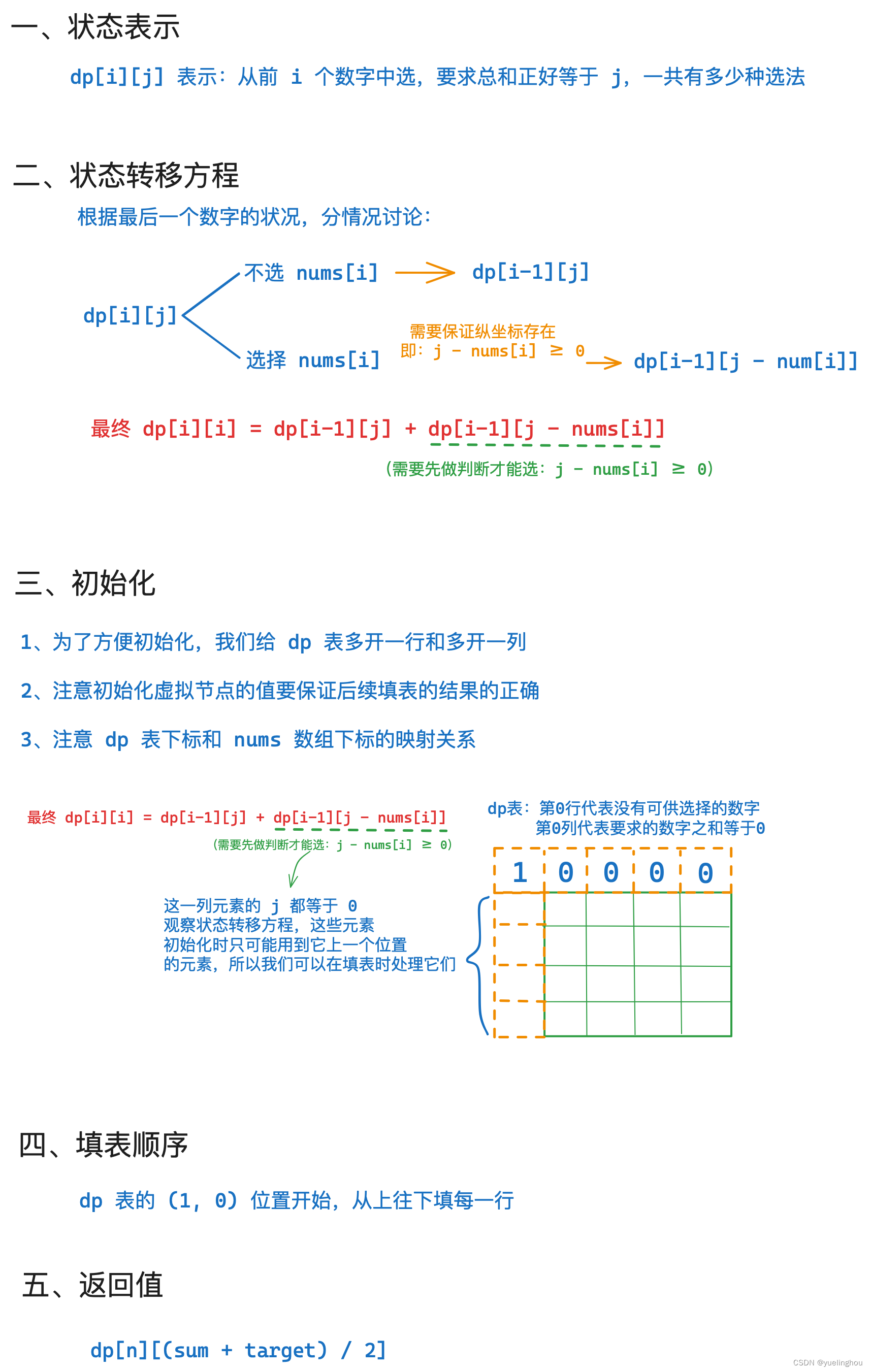
目标和

算法原理
代码编写
// 未优化版本
class Solution
{
public:
int findTargetSumWays(vector<int>& nums, int target)
{
// 0、预处理
int n = nums.size(), sum = 0;
for(const auto e : nums) sum += e;
int aim = (sum + target) / 2;
if(aim < 0 || (sum + target) % 2) return 0;
// 1、建表
vector<vector<int>> dp(n + 1, vector<int>(aim + 1));
// 2、初始化
dp[0][0] = 1;
// 3、填表
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= aim; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j >= nums[i - 1]) dp[i][j] += dp[i - 1][j - nums[i - 1]];
}
// 4、返回值
return dp[n][aim];
}
};
/*
- 时间复杂度:O(n * (sum + target))
- 空间复杂度:O(n * (sum + target))
*/
// 空间优化版本
// 1、删除横坐标
// 2、修改纵坐标的遍历顺序
class Solution
{
public:
int findTargetSumWays(vector<int>& nums, int target)
{
// 0、预处理
int n = nums.size(), sum = 0;
for(const auto e : nums) sum += e;
int aim = (sum + target) / 2;
if(aim < 0 || (sum + target) % 2) return 0;
// 1、建表
vector<int> dp(aim + 1);
// 2、初始化
dp[0] = 1;
// 3、填表
for(int i = 1; i <= n; ++i)
for(int j = aim; j >= nums[i - 1]; --j)
dp[j] += dp[j - nums[i - 1]];
// 4、返回值
return dp[aim];
}
};
/*
- 时间复杂度:O(n * (sum + target))
- 空间复杂度:O(sum + target)
*/
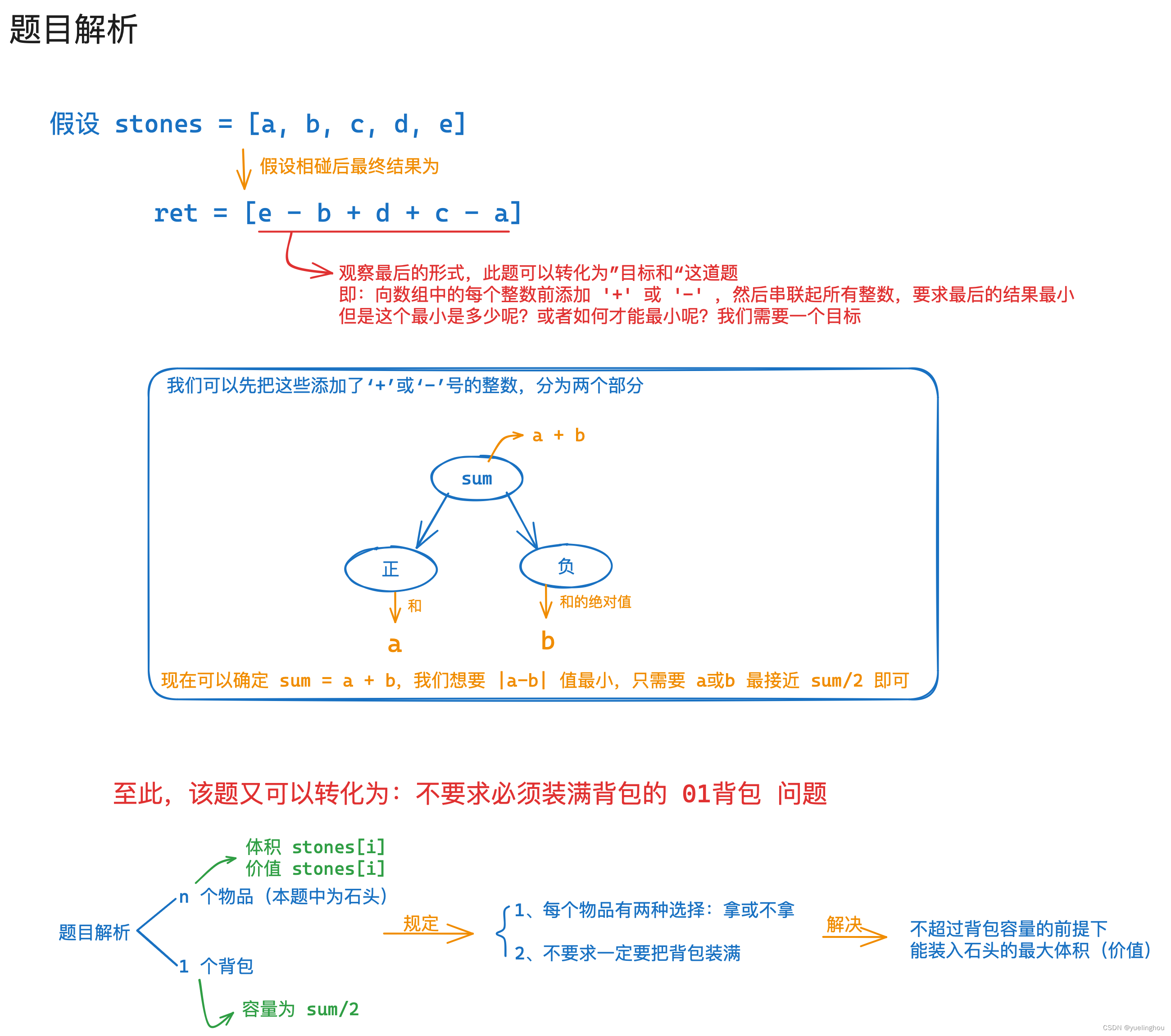
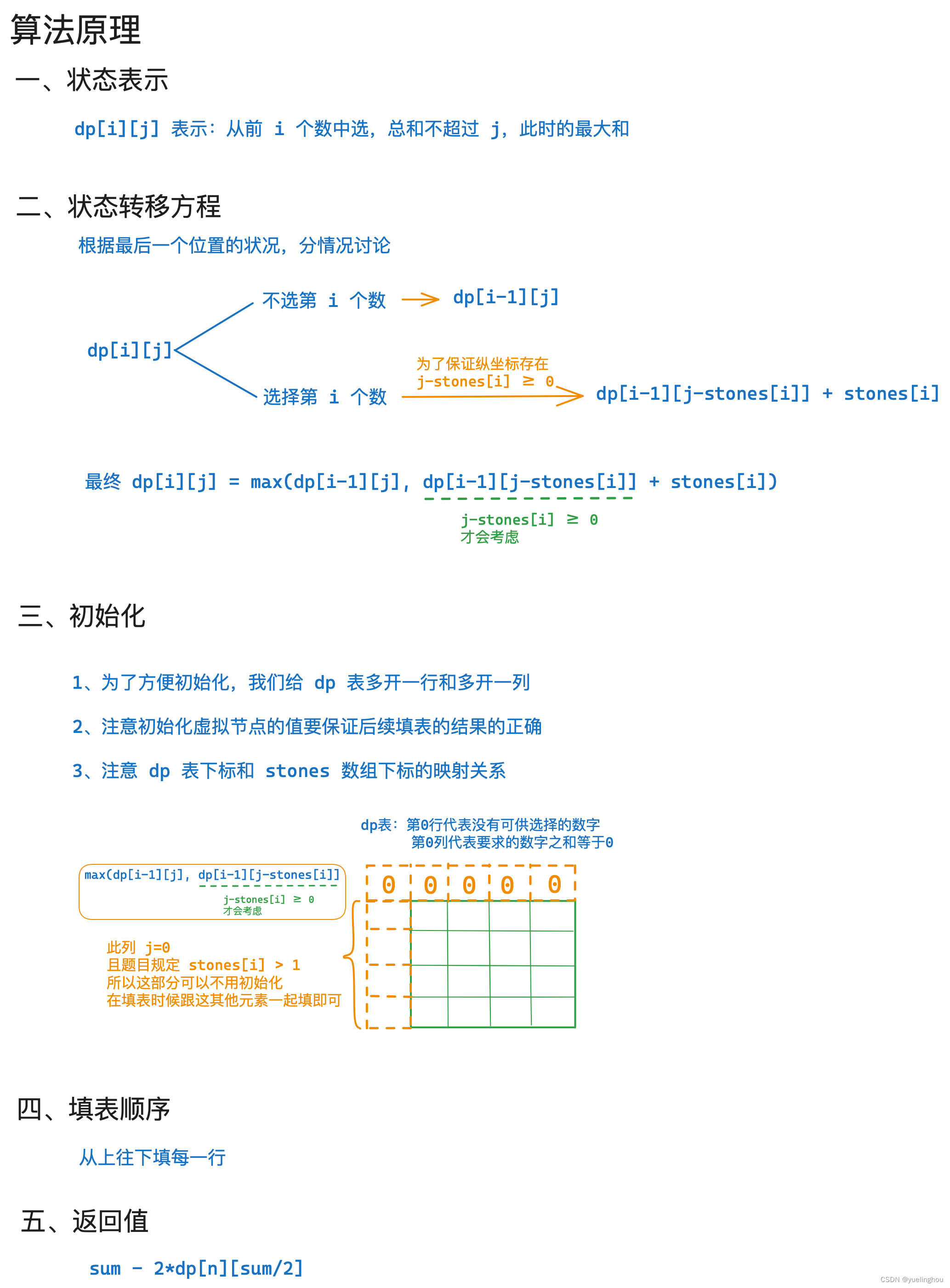
最后一块石头的重量 II

代码编写
// 未优化版本
class Solution
{
public:
int lastStoneWeightII(vector<int>& stones)
{
// 0、预处理
int sum = 0;
for(const auto e : stones) sum += e;
int n = stones.size(), half = sum / 2;
// 1、建表 && 初始化
vector<vector<int>> dp(n + 1, vector<int>(half + 1));
// 2、填表
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= half; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j >= stones[i - 1]) dp[i][j] = max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]);
}
// 3、返回值
return sum - 2 * dp[n][half];
}
};
/*
- 时间复杂度:O(n * sum)
- 空间复杂度:O(n * sum)
*/
//------------------------------------------------
// 空间优化版本
// - 删除 dp 表中的横坐标
// - 修改纵坐标遍历顺序
class Solution
{
public:
int lastStoneWeightII(vector<int>& stones)
{
// 0、预处理
int sum = 0;
for(const auto e : stones) sum += e;
int n = stones.size(), half = sum / 2;
// 1、建表 && 初始化
vector<int> dp(half + 1);
// 2、填表
for(int i = 1; i <= n; ++i)
for(int j = half; j >= stones[i - 1]; --j)
dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);
// 3、返回值
return sum - 2 * dp[half];
}
};
/*
- 时间复杂度:O(n * sum)
- 空间复杂度:O(sum)
*/
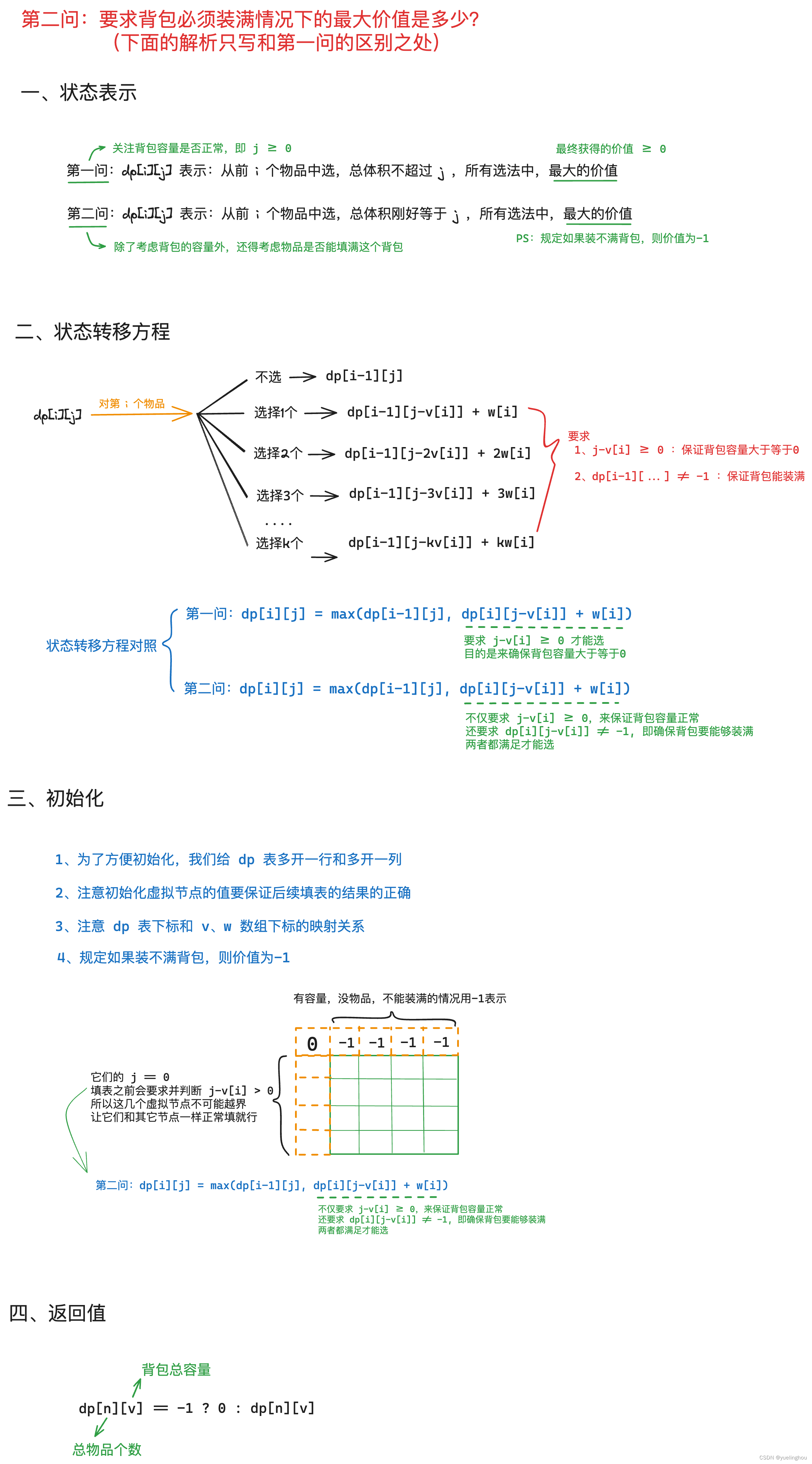
3.【模板】完全背包

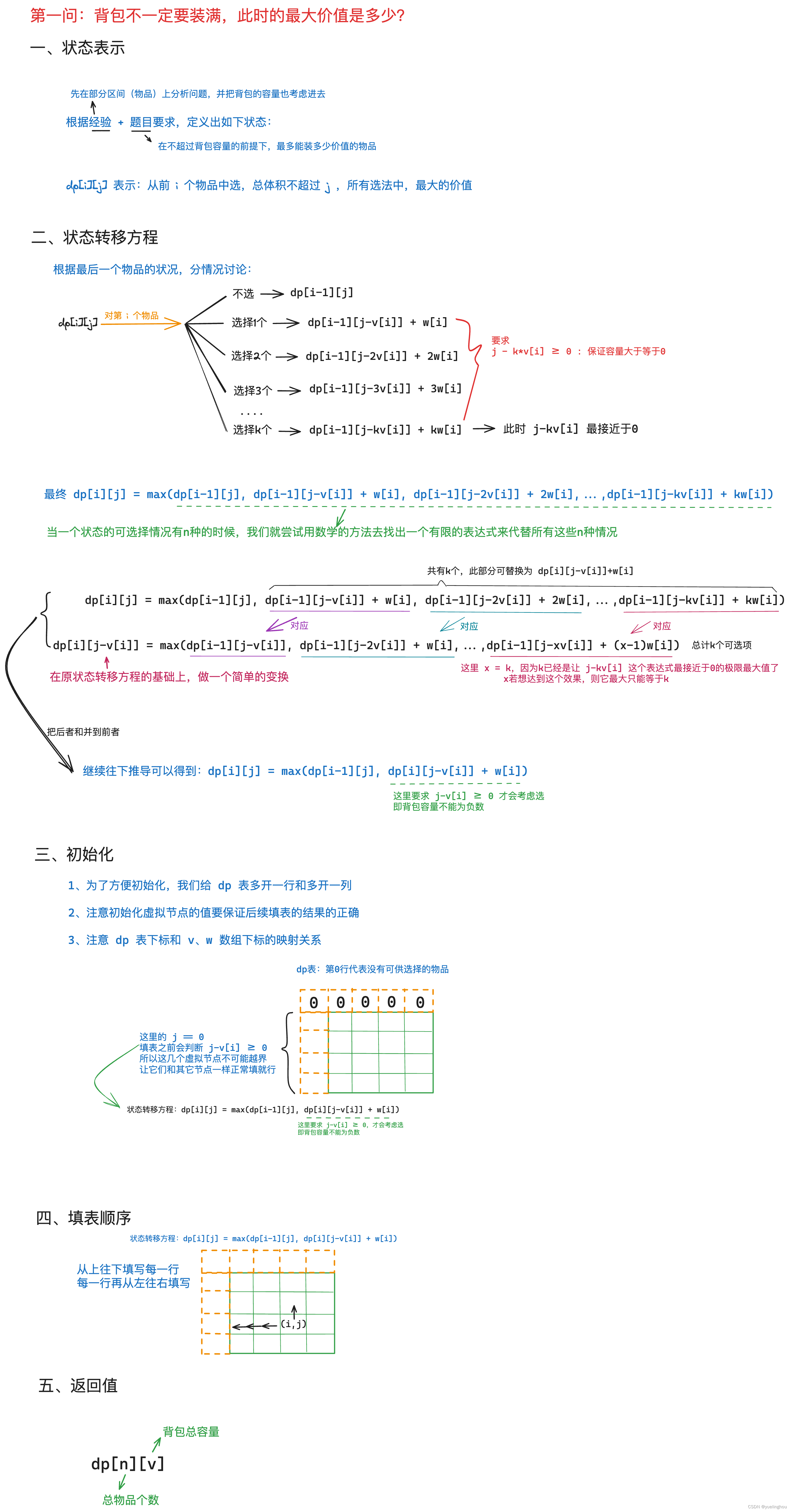
算法原理(第一问)
算法原理(第二问)
优化
代码编写
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
// 1、初始化
int n = 0, V = 0;
cin >> n >> V;
// n 个物品的体积和价值表,其中第 0 个位置仅仅用来占位
vector<int> v(n + 1), w(n + 1);
for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
// 2、建表
vector< vector<int> > dp(n + 1, vector<int>(V + 1));
// 解决第一问
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= V; ++j)
{
dp[i][j] = dp[i-1][j];
if(j >= v[i]) dp[i][j] = max(dp[i][j], dp[i][j-v[i]] + w[i]);
}
cout << dp[n][V] << endl;
// 解决第二问
for(int j = 1; j <= V; ++j) dp[0][j] = -1;
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= V; ++j)
{
dp[i][j] = dp[i-1][j];
if(j >= v[i] && dp[i][j-v[i]] != -1) dp[i][j] = max(dp[i][j], dp[i][j-v[i]] + w[i]);
}
cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
return 0;
}
/*
- 时间复杂度:O(nV)
- 空间复杂度:O(nV)
*/
//---------------------------------------------------------------
// 空间优化版本
// 1. 删除横坐标
// 2. 纵坐标从左往右遍历
int main()
{
// 1、初始化
int n = 0, V = 0;
cin >> n >> V;
// n 个物品的体积和价值表,其中第 0 个位置仅仅用来占位
vector<int> v(n + 1), w(n + 1);
for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
// 2、建表
vector<int> dp(V + 1);
// 解决第一问
for(int i = 1; i <= n; ++i)
for(int j = v[i]; j <= V; ++j)
dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
cout << dp[V] << endl;
//解决第二问
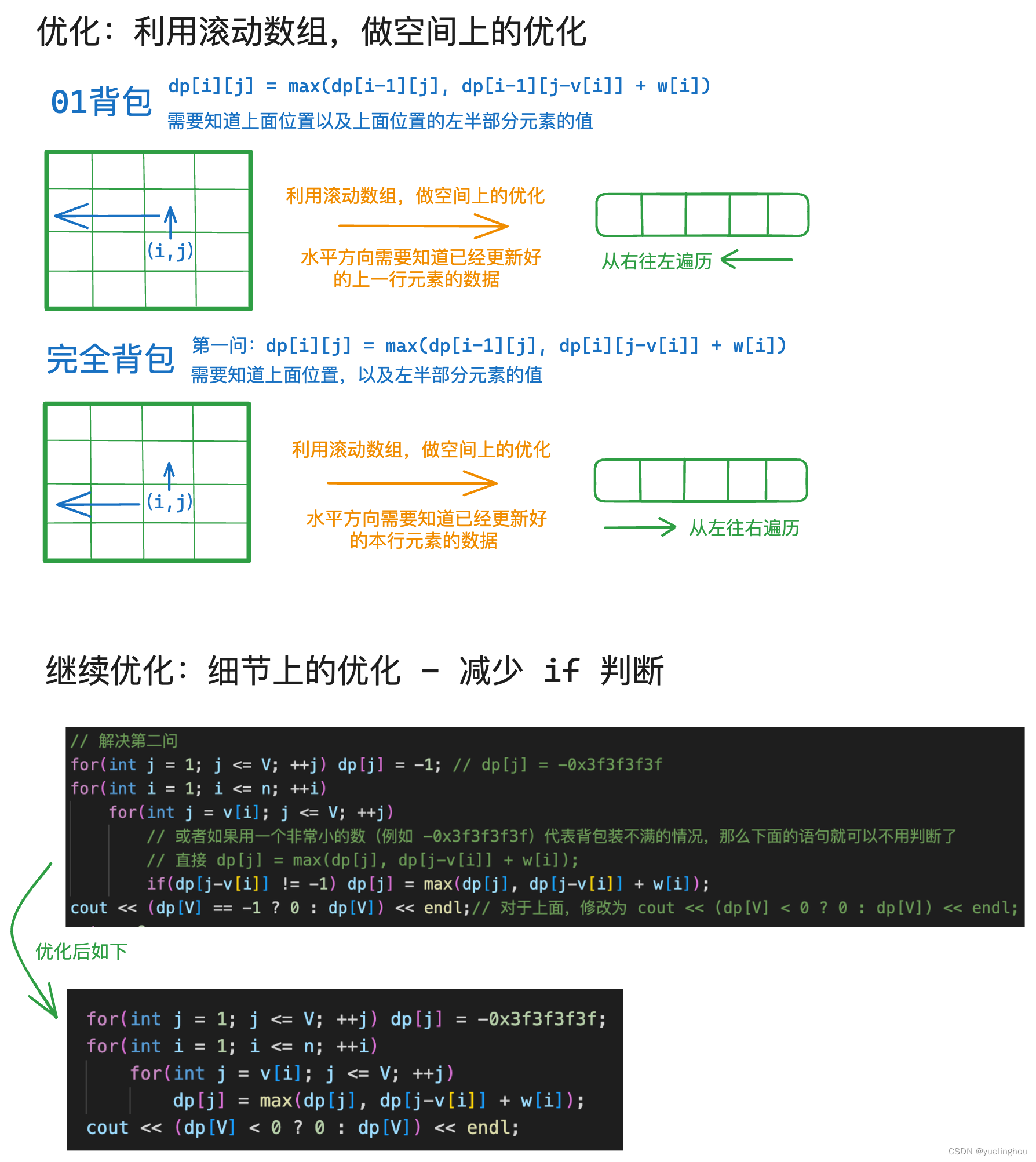
for(int j = 1; j <= V; ++j) dp[j] = -1; // 继续优化:dp[j] = -0x3f3f3f3f
for(int i = 1; i <= n; ++i)
for(int j = v[i]; j <= V; ++j)
// 或者如果用一个非常小的数(例如 -0x3f3f3f3f)代表背包装不满的情况,那么下面的语句就可以不用判断了
// 直接 dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
if(dp[j-v[i]] != -1) dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
cout << (dp[V] == -1 ? 0 : dp[V]) << endl;// 对于上面,修改为 cout << (dp[V] < 0 ? 0 : dp[V]) << endl;
return 0;
}
/*
- 时间复杂度:O(nV)
- 空间复杂度:O(V)
*/
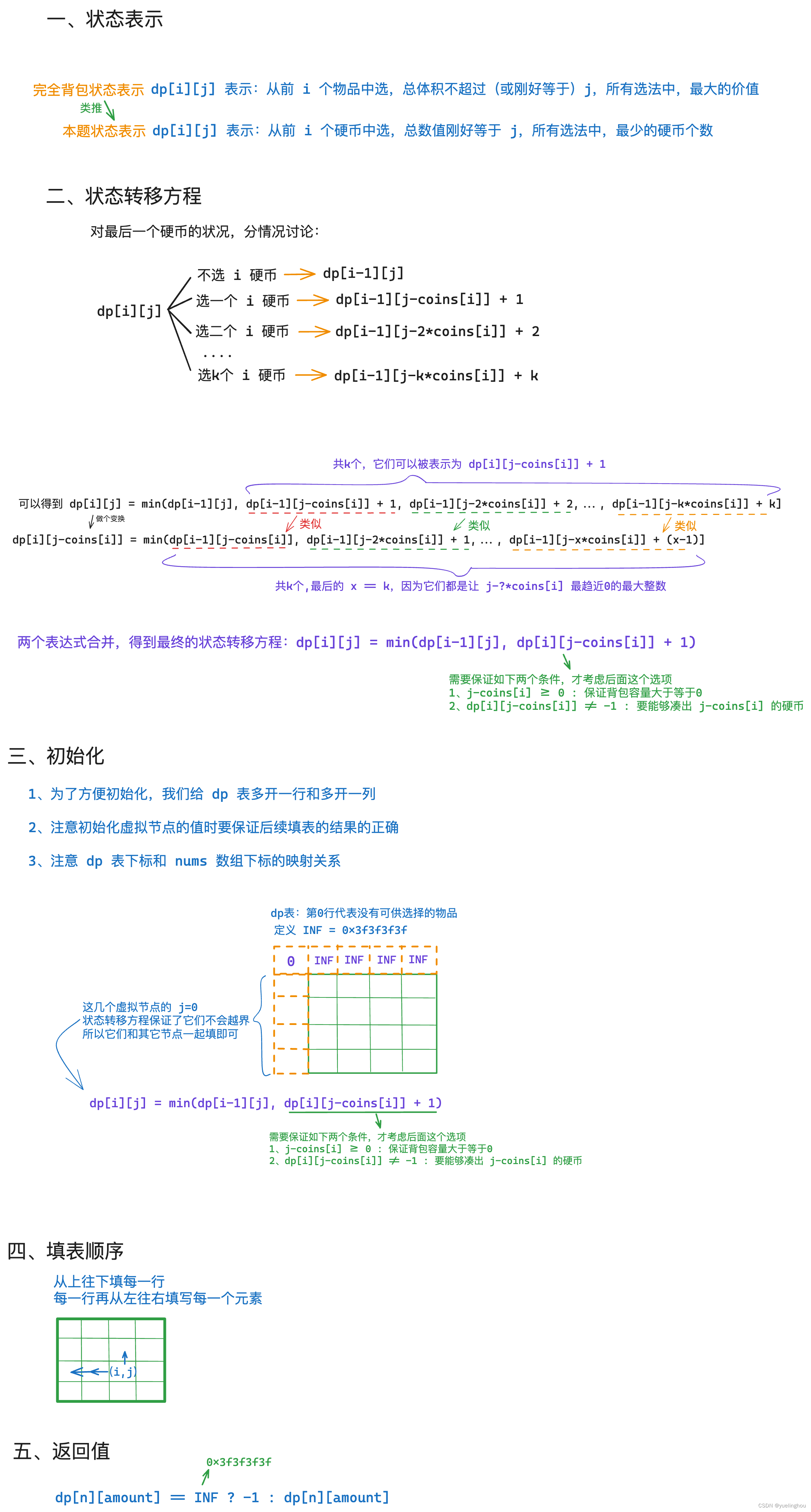
零钱兑换

算法原理
代码编写
// 未优化版本
class Solution
{
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector<int>& coins, int amount)
{
// 1、建表
int n = coins.size();
vector<vector<int>> dp(n + 1, vector<int>(amount + 1));
// 2、初始化
for(int j = 1; j <= amount; ++j) dp[0][j] = INF;
// 3、填表
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= amount; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j >= coins[i-1] && dp[i][j - coins[i-1]] != INF) dp[i][j] = min(dp[i][j], dp[i][j - coins[i-1]] + 1);
}
// 4、返回值
return dp[n][amount] == INF ? -1 : dp[n][amount];
}
};
/*
- 时间复杂度:O(n * amount)
- 空间复杂度:O(n * amount)
*/
// -----------------------------------------------------------
// 优化版本
// 1、删除 dp 中的横坐标
// 2、纵坐标从左往右的顺序遍历
class Solution
{
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector<int>& coins, int amount)
{
// 1、建表
int n = coins.size();
vector<int> dp(amount + 1, INF);
// 2、初始化
dp[0] = 0;
// 3、填表
for(int i = 1; i <= n; ++i)
for(int j = coins[i-1]; j <= amount; ++j)
dp[j] = min(dp[j], dp[j - coins[i-1]] + 1);
// 4、返回值
return dp[amount] == INF ? -1 : dp[amount];
}
};
/*
- 时间复杂度:O(n * amount)
- 空间复杂度:O(amount)
*/
零钱兑换II

算法原理

代码编写
// 未优化版本
class Solution
{
public:
int change(int amount, vector<int>& coins)
{
// 1、建表
int n = coins.size();
vector< vector<int> > dp(n + 1, vector<int>(amount + 1));
// 2、初始化
dp[0][0] = 1;
// 3、填表
for(int i = 1; i <= n; ++i)
for(int j = 0; j <= amount; ++j)
{
dp[i][j] = dp[i - 1][j];
if(j >= coins[i - 1]) dp[i][j] += dp[i][j - coins[i - 1]];
}
// 4、返回值
return dp[n][amount];
}
};
/*
- 时间复杂度:O(n * amount)
- 空间复杂度:O(n * amount)
*/
// -----------------------------------------------------------------------------
// 利用滚动数组进行空间优化
// 1、删除 dp 表的横坐标
// 2、纵坐标从左往右遍历
class Solution
{
public:
int change(int amount, vector<int>& coins)
{
// 1、建表
int n = coins.size();
vector<int> dp(amount + 1);
// 2、初始化
dp[0] = 1;
// 3、填表
for(const auto e : coins)
for(int j = e; j <= amount; ++j)
dp[j] += dp[j - e];
// 4、返回值
return dp[amount];
}
};
/*
- 时间复杂度:O(n * amount)
- 空间复杂度:O(amount)
*/
4. 二维费用的背包问题
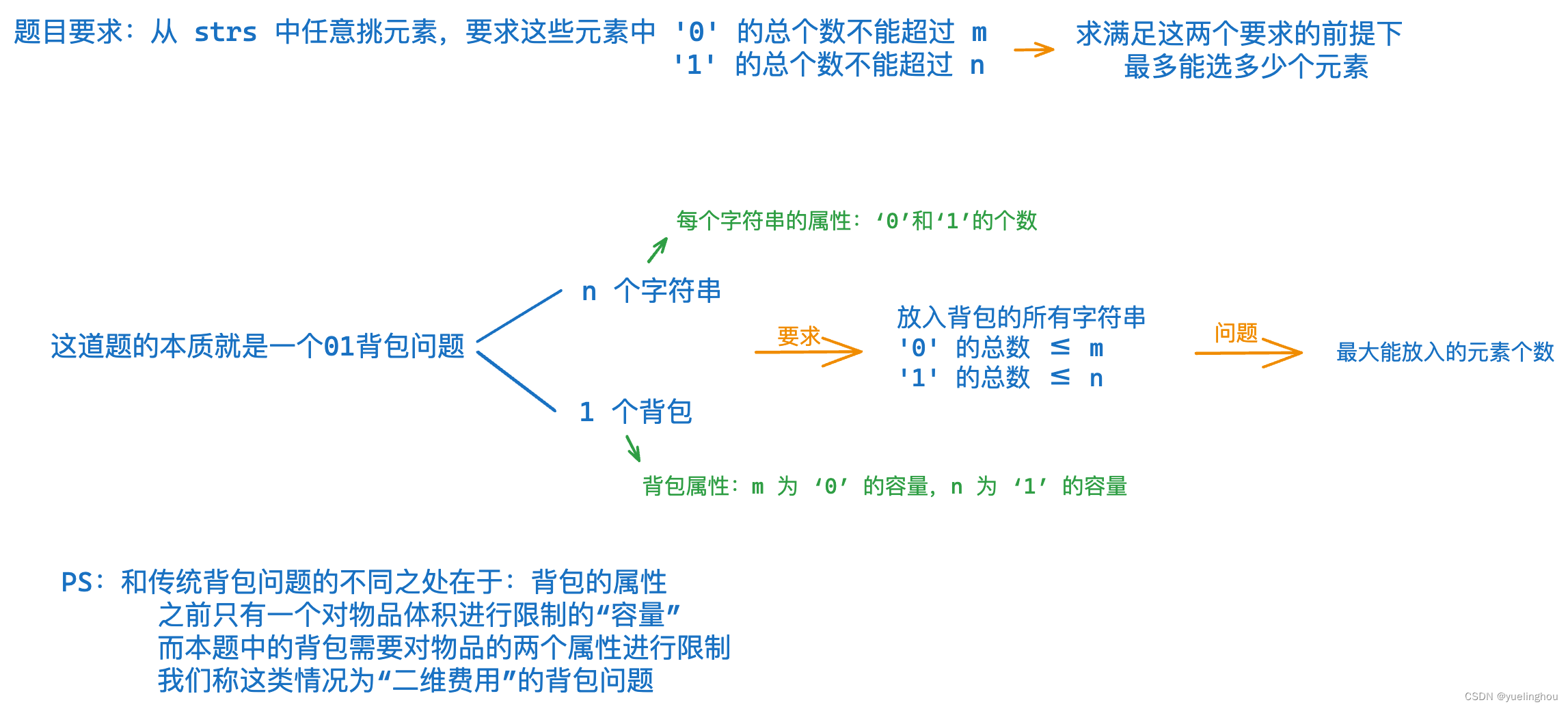
一和零

题目解析
算法原理

代码编写
// 未优化版本
class Solution
{
public:
int findMaxForm(vector<string>& strs, int m, int n)
{
// 1、建表 && 初始化
int len = strs.size();
vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1)));
// 2、填表
for(int i = 1; i <= len; ++i)
{
// 计算 strs[i] 中,'0' 和 '1' 的个数
int a = 0, b = 0;
for(const auto e : strs[i - 1])
{
if(e == '0') ++a;
else ++b;
}
// 继续遍历其它维度
for(int j = 0; j <= m; ++j)
for(int k = 0; k <= n; ++k)
{
dp[i][j][k] = dp[i-1][j][k];
if(j >= a && k >= b) dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-a][k-b] + 1);
}
}
// 3、返回值
return dp[len][m][n];
}
};
/*
- 时间复杂度:O(len * m * n)
- 空间复杂度:O(len * m * n)
*/
// ----------------------------
// 利用滚动数组进行空间优化
// 1、删除 dp 表的横坐标
// 2、修改 j 和 k 维度的遍历顺序(改为从大到小)
class Solution
{
public:
int findMaxForm(vector<string>& strs, int m, int n)
{
// 1、建表 && 初始化
int len = strs.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 2、填表
for(int i = 0; i < len; ++i)
{
// 计算 strs[i] 中,'0' 和 '1' 的个数
int a = 0, b = 0;
for(const auto e : strs[i])
{
if(e == '0') ++a;
else ++b;
}
// 继续遍历其它维度
for(int j = m; j >= a; --j)
for(int k = n; k >= b; --k)
dp[j][k] = max(dp[j][k], dp[j-a][k-b] + 1);
}
// 3、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(len * m * n)
- 空间复杂度:O(len * m * n)
*/
// ----------------------------
// 利用滚动数组进行空间优化
// 1、删除 dp 表的横坐标
// 2、修改 j 和 k 维度的遍历顺序(改为从大到小)
class Solution
{
public:
int findMaxForm(vector<string>& strs, int m, int n)
{
// 1、建表 && 初始化
int len = strs.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 2、填表
for(int i = 0; i < len; ++i)
{
// 计算 strs[i] 中,'0' 和 '1' 的个数
int a = 0, b = 0;
for(const auto e : strs[i])
{
if(e == '0') ++a;
else ++b;
}
// 继续遍历其它维度
for(int j = m; j >= a; --j)
for(int k = n; k >= b; --k)
dp[j][k] = max(dp[j][k], dp[j-a][k-b] + 1);
}
// 3、返回值
return dp[m][n];
}
};
/*
- 时间复杂度:O(len * m * n)
- 空间复杂度:O(m * n)
*/
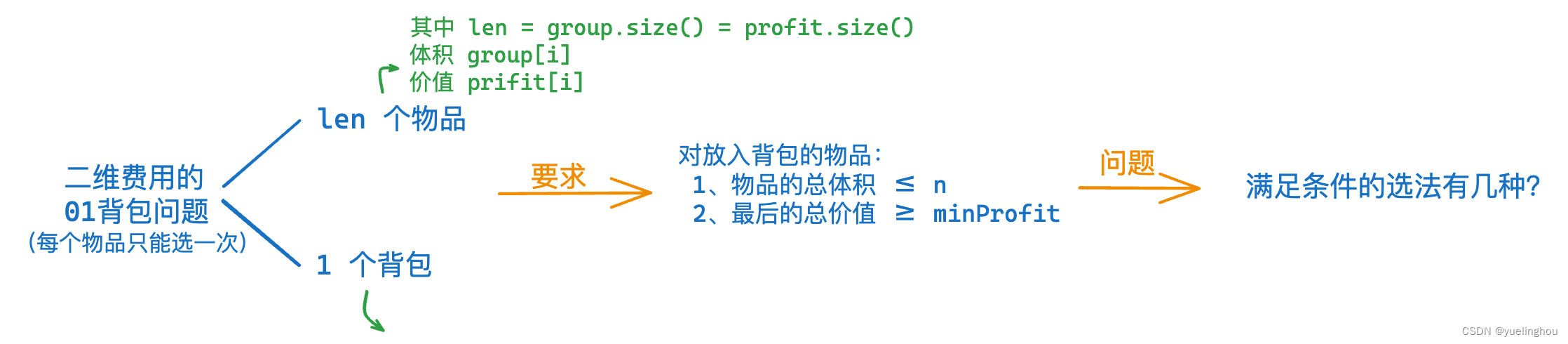
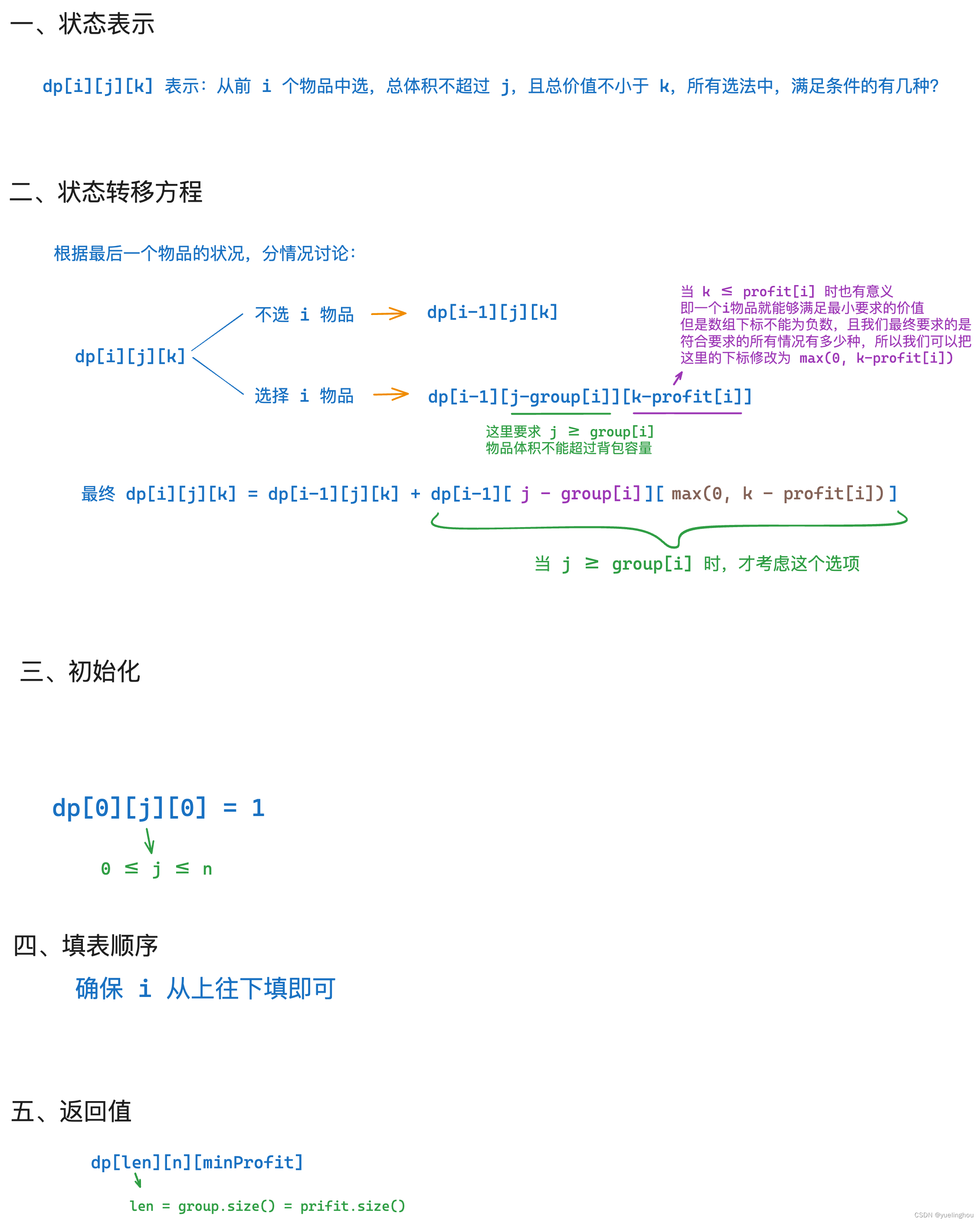
盈利计划

题目解析
算法原理
代码编写
// 未优化版本
class Solution
{
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
{
// 1、建表
int len = group.size();
vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(n + 1, vector<int>(minProfit + 1)));
// 2、初始化
for(int j = 0; j <= n; ++j) dp[0][j][0] = 1;
// 3、填表
for(int i = 1; i <= len; ++i)
for(int j = 0; j <= n; ++j)
for(int k = 0; k <= minProfit; ++k)
{
dp[i][j][k] = dp[i - 1][j][k];
if(j >= group[i - 1]) dp[i][j][k] += dp[i - 1][j - group[i - 1]][max(0, k - profit[i - 1])];
dp[i][j][k] %= (int)(1e9 + 7);
}
// 4、返回值
return dp[len][n][minProfit];
}
};
/*
- 时间复杂度:O(len * n * profit)
- 空间复杂度:O(len * n * profit)
*/
// ---------------------
// 利用滚动数组进行空间优化
// 1、删除 dp 表的横坐标
// 2、修改 j 和 k 维度的遍历顺序(改为从大到小)
class Solution
{
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
{
int len = group.size();
// 1、建表
vector<vector<int>> dp(n + 1, vector<int>(minProfit + 1));
for(int j = 0; j <= n; ++j) dp[j][0] = 1;
// 2、填表
for(int i = 0; i < len; ++i)
for(int j = n; j >= group[i]; --j)
for(int k = minProfit; k >= 0; --k)
{
dp[j][k] += dp[j - group[i]][max(0, k - profit[i])];
dp[j][k] %= (int)(1e9 + 7);
}
// 3、返回值
return dp[n][minProfit];
}
};
/*
- 时间复杂度:O(len * n * profit)
- 空间复杂度:O(n * profit)
*/
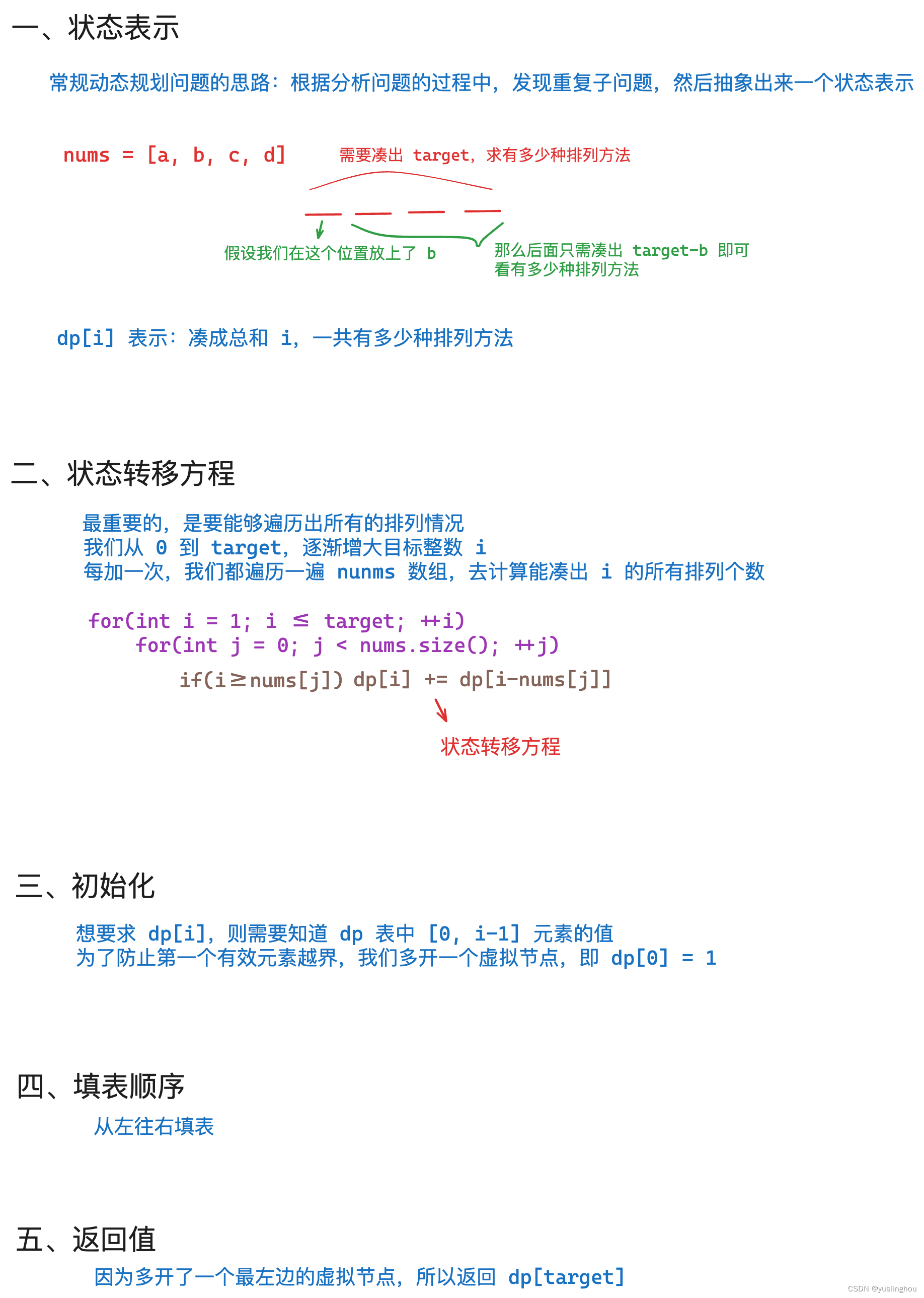
5. 似包非包问题 - 组合总和IV

题目解析

算法原理
代码编写
// 未优化版本
class Solution
{
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
{
// 1、建表
int len = group.size();
vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(n + 1, vector<int>(minProfit + 1)));
// 2、初始化
for(int j = 0; j <= n; ++j) dp[0][j][0] = 1;
// 3、填表
for(int i = 1; i <= len; ++i)
for(int j = 0; j <= n; ++j)
for(int k = 0; k <= minProfit; ++k)
{
dp[i][j][k] = dp[i - 1][j][k];
if(j >= group[i - 1]) dp[i][j][k] += dp[i - 1][j - group[i - 1]][max(0, k - profit[i - 1])];
dp[i][j][k] %= (int)(1e9 + 7);
}
// 4、返回值
return dp[len][n][minProfit];
}
};
/*
- 时间复杂度:O(len * n * profit)
- 空间复杂度:O(len * n * profit)
*/
// ---------------------
// 利用滚动数组进行空间优化
// 1、删除 dp 表的横坐标
// 2、修改 j 和 k 维度的遍历顺序(改为从大到小)
class Solution
{
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
{
int len = group.size();
// 1、建表
vector<vector<int>> dp(n + 1, vector<int>(minProfit + 1));
for(int j = 0; j <= n; ++j) dp[j][0] = 1;
// 2、填表
for(int i = 0; i < len; ++i)
for(int j = n; j >= group[i]; --j)
for(int k = minProfit; k >= 0; --k)
{
dp[j][k] += dp[j - group[i]][max(0, k - profit[i])];
dp[j][k] %= (int)(1e9 + 7);
}
// 3、返回值
return dp[n][minProfit];
}
};
/*
- 时间复杂度:O(len * n * profit)
- 空间复杂度:O(n * profit)
*/
6. 卡特兰数 - 不同的二叉搜索树
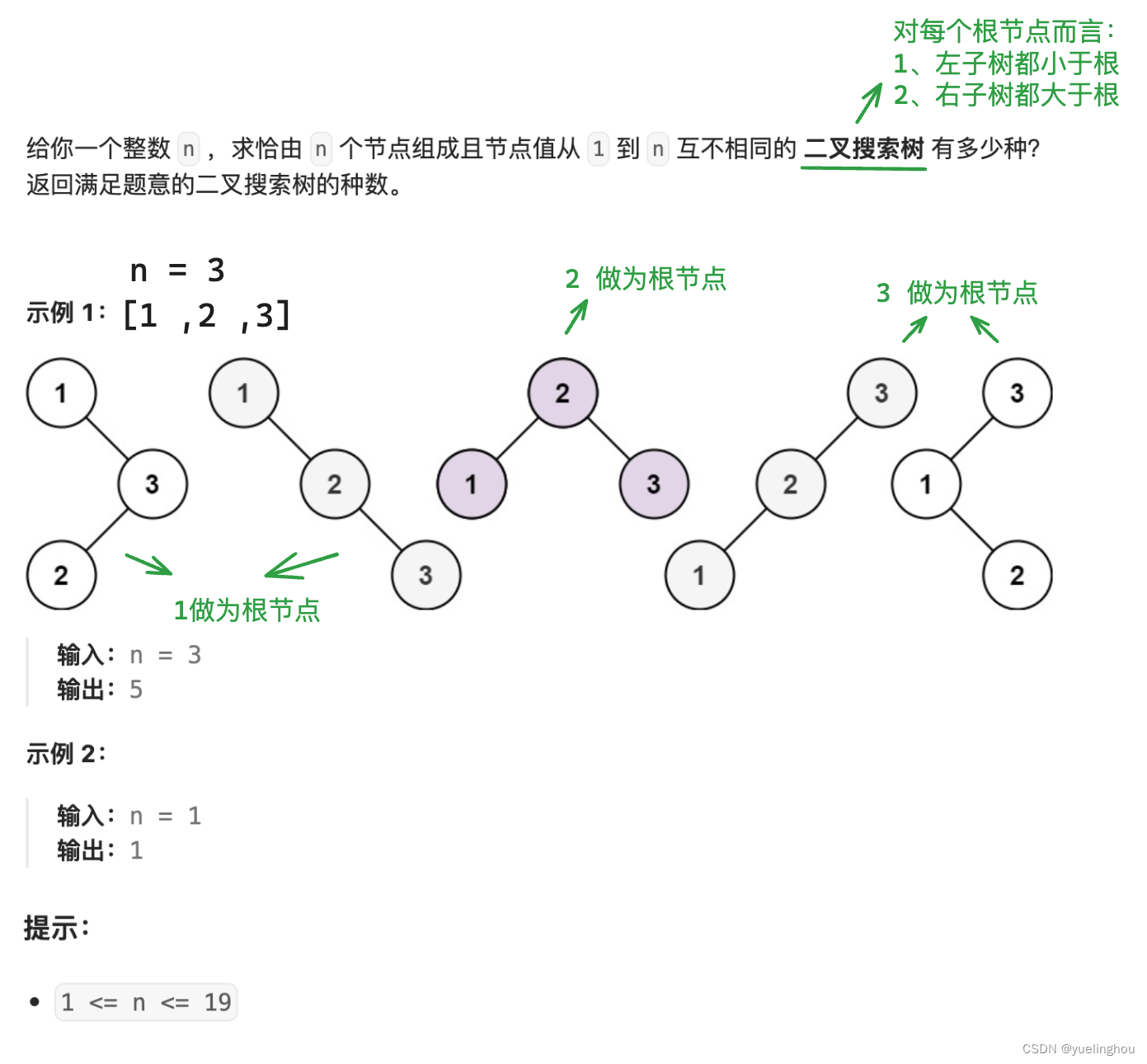
算法原理
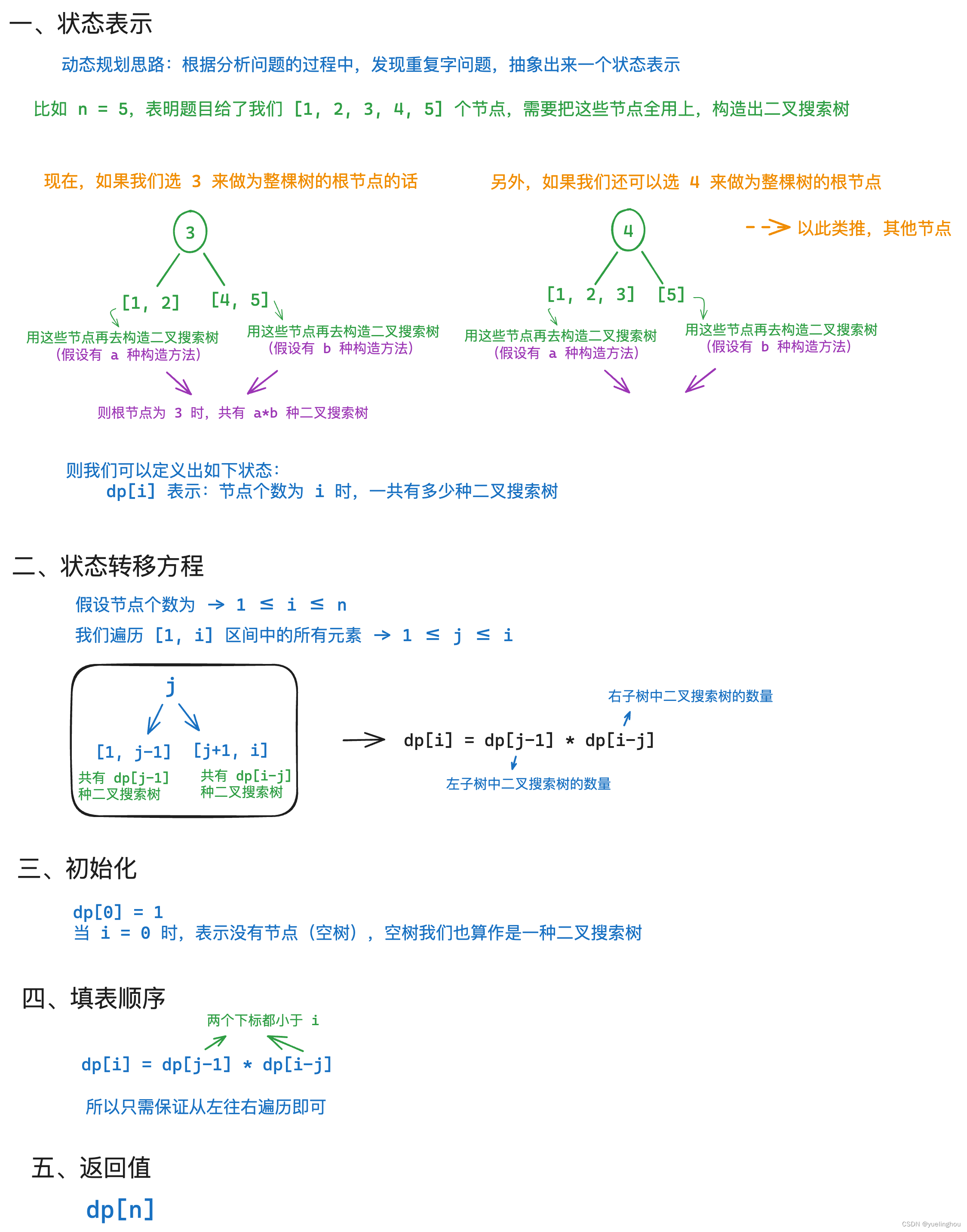
代码编写
class Solution
{
public:
int numTrees(int n)
{
// 1、建表
vector<int> dp(n + 1);
// 2、初始化
dp[0] = 1;
// 3、填表
for(int i = 1; i <= n; ++i) // i 代表节点数量
for(int j = 1; j <= i; ++j)// j 代表根节点
dp[i] += dp[j-1] * dp[i-j];
// 4、返回值
return dp[n];
}
};
/*
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
*/























 1977
1977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








