图的应用—求解最短路径（BFS、Dijkstra和Floyd算法）

BFS算法虽然可以求解最短路径问题，但是需要注意的是该算法只能求解非带权图的单源最短路径问题，或者说带权值相同且为1的图单源最短路径问题。

1、图的邻接矩阵存储结构定义

#define MaxVerNum 100            //顶点数目的最大值 
typedef struct{
	char Vex[MaxVerNum];     //顶点表
	int Edge[MaxVerNum][MaxVerNum];    //邻接矩阵，边表
	int vexnum,archnum;              //图的当前顶点数和弧数 
}Graph;

2、图的邻接表存储结构定义

#define MaxVerNum 100            //顶点数目的最大值 
typedef struct ArcNode{           //边表结点 
	int adjvex;                  //该弧所指向的顶点的位置
	struct ArcNode *next;        //指向下一条弧的指针 
	int num;                    //图的权值 
}ArcNode; 
typedef struct VNode{           //顶点表信息 
	char data;                  //顶点信息 
	ArcNode *first;              //指向第一条依附于该顶点的弧的指针 
}VNode,AdjList[MaxVerNum];
typedef struct{
	AdjList vertices;            //邻接表
	int vexnum,arcnum;             //图的顶点数和弧数 
}Graph;

3、BFS算法求解非带权图的单源最短路径

//BFS算法求解非带权图单源最短路径问题
void BFS_MIN_Distance(Graph G,int u)    //求到u的单源最短路径 
{
	for(int i=0;i<G.vexnum;i++)
	{
		d[i]=INF;         //初始化路径长度
		path[i]=-1;       //初始化到达每个顶点的前驱结点 
	}	
	visit[u]=true;
	d[u]=0;            //自身到自身的距离为0 
	EnQueue(Q,u);
	while(!isEmpty(Q))
	{
		DeQueue(Q,u);
		for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
		{
			if(!visit[w])
			{
				visit[w]=true;
				d[w]=d[u]+1;         //路径长度加1 
				path[w]=u;           //最短路径是从u到w 
				EnQueue(Q,w);       //w入队 
			}
		}
	}
} 

由于BFS算法的应用局限，所以对于带权值（正值）的图， 我们需要求解其单源最短路径的时候，就可以使用Dijkstra算法。

单源最短路径是指：图中某一顶点到其他各顶点的最短路径。

4、Dijkstra算法的定义 

Dijsktra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层扩展，直到扩展到终点为止。在无向图G=(V,E)中，假设每条边E[i]的长度为w[i]，找到由顶点v0到其余各点的最短路径。 

5、Dijkstra算法的基本思想 

1、把路径长度递增次序产生最短路径算法。

2、把V分为两组：

S：已求出最短路径的顶点的集合，初始时S中只有一个源点，以后每求得一条最短路径就将其加入到集合S中，直到所有顶点都加入到S中；

V-S=T：尚未确定最短路径的顶点集合；

3、将T中顶点按最短路径递增的次序加入到S中，保证：从源点V0到S中各顶点的最短路径长度都不大于从V0到T中任何顶点的最短路径长度。

4、每个顶点对应一个距离值：

S中顶点：从V0到此顶点的最短路径长度；

T中顶点：从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度；

6、具体实现过程

首先将其全部初始化为无穷大（除了源点到源点之外）：

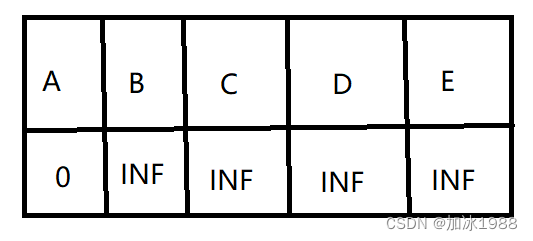
在表中选择一个路径最短的点a，从a出发，a到自己的距离是0，它往外有三条边，更新a到b,c,d的最短距离，此时a被标记，则此后a都不会再被访问，此时该表更新为：

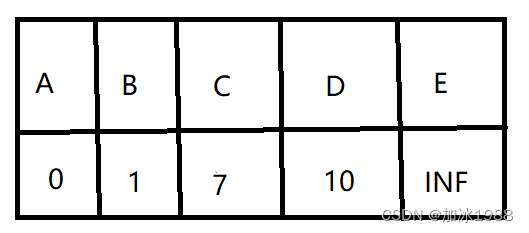
再在这张表中选择一个最短距离，是A->B，选出B作为新的起点，它有两条边分别是到达C,E，由于从B到C的距离是2，则从源点经过B到达C的最短距离是3，比之前的要小，所以更新最短距离，这时B也被标记，B不会再被访问。

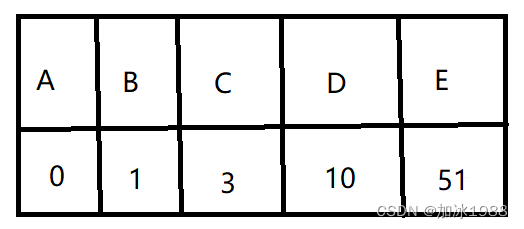
再在这张表中选择一个最短距离，从AàC，则选择C点作为新的起点，从C出发有2条边，分别到达D,E，由于从A经过C到E的最短距离是23，小于之前的51，所以更新最短距离，从A经过C到达D的最短距离是8，小于之前的10，更新最短距离，则此时C被标记，C之后便不会再被访问。

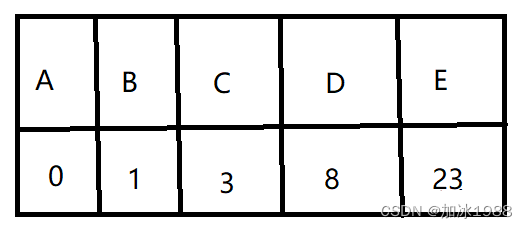
再在这张表中选择一个最短距离，从A->D，所以选择D作为新的起点，从D只有一条边，到达E，则此时从A经过B,C,D到达E的最短距离是11，小于之前的23，所以更新最短距离，则此时D被标记，D不会再被访问。

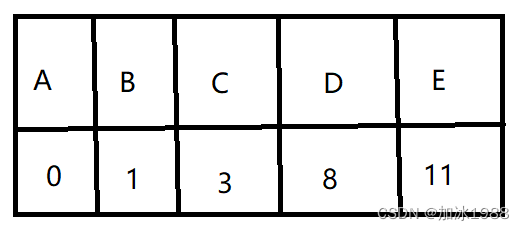
再在这张表中选择一个最短距离，只有A->E，由于它并没有没访问的边，所以循环跳出，整个遍历结束！

所以这个有向图的单源最短路径是0，1，3，8，11。

 再需要更新最短路径的时候，使用数组tar记录下到达当前顶点的前一个顶点，也就是最佳路径的弧尾和弧头。然后使用深度优先遍历递归查找每个顶点到源点的最短路径。

7、给出Dijkstra算法求解单源最短路径的实例 

【问题描述】

给定一个n个顶点，m条有向边的带非负权图，请计算从s出发，到图中各点的距离。

【输入输出及示例】

输入：顶点数n，边数m，源点s，m条边以（p,q,weight）形式输入，分别表示弧尾、弧头和弧长;

输出：源点到每个点的距离，同时输出源点到每个点的路径。

示例1：

输入：顶点数：7，边数：10，源点：1

      弧尾、弧头、弧长为：

     1 2 13

      1 3 8

      1 5 30

      1 7 32

      2 6 9

      2 7 7

      3 4 5

      4 5 6

      5 6 2

      6 7 17

             

输出：源点到顶点1的最短路径长度是：0

      源点到顶点1的最短路径是：1

      源点到顶点2的最短路径长度是：13

      源点到顶点2的最短路径是：1 2

      源点到顶点3的最短路径长度是：8

      源点到顶点3的最短路径是：1 3

      源点到顶点4的最短路径长度是：13

      源点到顶点4的最短路径是：1 3 4

      源点到顶点5的最短路径长度是：19

      源点到顶点5的最短路径是：1 3 4 5

      源点到顶点6的最短路径长度是：21

      源点到顶点6的最短路径是：1 3 4 5 6

      源点到顶点7的最短路径长度是：20

      源点到顶点7的最短路径是：1 2 7

 代码：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define INF 0X3F3F3F3F

//使用链式存储边，建图 
struct node{
	int begin;  //边的始点 
	int end;    //边的终点 
	int cost;   //边的代价 
	int next;   //当前边的下一条相邻边 
}e[1010]; 

int head[1010];   //head[i]存储与该点相邻的边
int dis[1010];    //存放源点到每个点的最短距离 
int visit[1010];  //标记哪些点被访问，访问的点被设为1 
int tar[1010];    //追踪最短路径

void dfs(int s,int v)   //输出最短路径 
{
	if(s==v)    //递归到源点，输出源点 
	{
		cout<<s<<" ";
		return ;
	}
	dfs(s,tar[v]);     //一直寻找到达该点的路径 
	cout<<v<<" ";
} 
int main()
{
	int n,m,s;
	cout<<"请输入顶点的个数、边的条数以及源点的位置: ";
	cin>>n>>m>>s;
	cout<<"请输入每条边的起点、始点和代价："<<endl;
	for(int i=1;i<=m;i++)   //存储边，建图 
	{
		cin>>e[i].begin>>e[i].end>>e[i].cost;
		int from=e[i].begin;     //记录当前是从哪个点发出 
		e[i].next=head[from];    //存储该点的下一条边 
		head[from]=i;           // 更新与该点的相邻的最后一条边（也就是当前边） 
	} 
	
	for(int i=1;i<=n;i++)  //初始化，先将每个距离设置为最大值 
	{
		dis[i]=INF;
	} 
	
	int begin=s;
	dis[begin]=0;   //自己到自己的最短距离为0 
	
	while(visit[begin]!=1)  //对每个点进行查找，直至所有点被标记完 
	{
		visit[begin]=1;   //没被访问，那就访问 
		for(int i=head[begin];i!=0;i=e[i].next)  //依次访问与当前起点相邻的边
		{
			if(dis[e[i].end]>dis[e[i].begin]+e[i].cost)  //更新不同起点到达该点的最短距离 
			{
				dis[e[i].end]=dis[e[i].begin]+e[i].cost;
				tar[e[i].end]=e[i].begin;   //存储当前点的前一个点 
			}
		} 
		
		int min1=INF;
		for(int i=1;i<=n;i++)   //每一次都寻找所有还没被标记的点中距离最小的点
		{
			if(visit[i]!=1&&dis[i]<min1)
			{
				min1=dis[i];
				begin=i;   //以距离最小的点为新的起点，从当前点出发 
			}
		}
	} 
	
	cout<<"源点到每个点的最短路径长度："<<endl;
	for(int i=1;i<=n;i++) 
	{
		cout<<"源点到顶点"<<i<<"的最短路径长度为："<<dis[i]<<endl;
		if(dis[i]==INF)   //说明不可达
		{
			cout<<"该点不可达！"<<endl<<endl;
		} 
		else
		{
			cout<<"源点到顶点"<<i<<"的最短路径是：";
			dfs(s,i);
			cout<<endl<<endl;
		}
	}
	return 0;
}

需要注意的是：Dijkstra算法虽然能求解带权图的单源最短路径问题，但是其权值只能是非负值，对于负权值该算法不一定能得到正确结果。 

8、Floyd算法求各顶点之间最短路径问题 

Floyd算法其实是基于动态规划的思想，在原路径中尝试加入顶点k作为中间顶点，得到的新路径与原路径长度比较，得到最短路径。

#define Maxsize 100
int path[Maxsize][Maxsize];       //记录某一顶点到另一顶点的中转矩阵
int A[Maxsize][Maxsize];          //记录从顶点i到顶点j的路径长度 
//初始化准备工作，初始化矩阵A和path 
for(int k=0;k<n;k++)     //列举中转点 
{
	for(int i=0;i<n;i++)    //遍历整个矩阵的行和列 
	{
		for(int j=0;j<n;j++)
		{
			if(A[i][j]>A[i][k]+A[k][j])
			{
				A[i][j]=A[i][k]+A[k][j];    //更新最短路径 
				path[i][j]=k;              //记录中转点 
			}
		}
	}
}

Floyd算法的时间复杂度为O(|V|^3)，空间复杂度为O(|V|^2)。该算法可以解决图中带负权值的问题，但是其不允许包含带负权值的边组成的回路，因为这种图有可能不存在最短路径。