【算法笔记】：区间覆盖问题：贪心算法

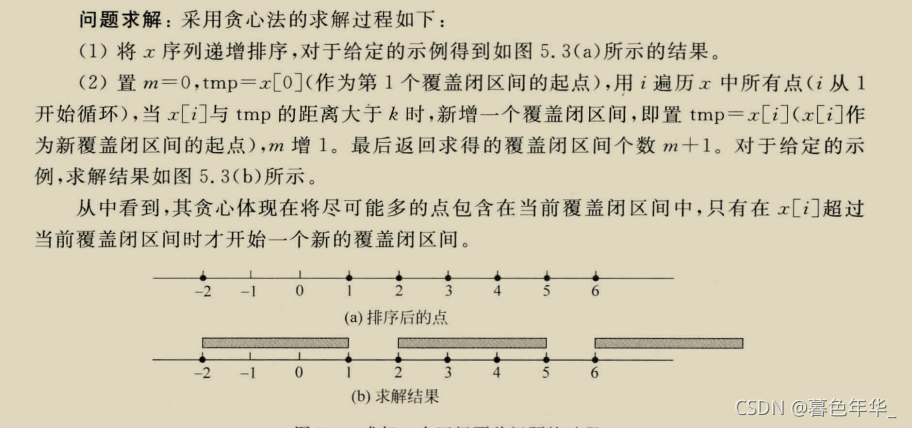
 证明贪心算法的正确性：

下面证明：

（1）最优子结构：

假设结果有n个区间，去掉最后一个区间及对应的点，则前n-1个区间仍然是覆盖所有点的所用的最少区间（最优解的子结构是子问题的最优解）

证明：

cut&paste(剪切法，本质是反证法)

假设一共M个点，覆盖所有的点至少需要n个区间，最后一个区间覆盖m个点

假设前n-1个区间不是子问题的最优解，即n-1不是覆盖前M-m个点的最少区间个数，则一定存在N，是覆盖M-m个点的最优解，且N<n-1，用N替代n-1,可得覆盖所有点最少区间个数为N+1<n

和假设至少需要n个区间矛盾。所以，问题具有最优子结构

（2）贪心选择性质:

 

 

参考：
算法设计与分析

百度百科