相关信息:
标题:FAST-LIVO2: Fast, Direct LiDAR-Inertial-Visual Odometry
作者:Chunran Zheng, Wei Xu, Zuhao Zou, Tong Hua, Chongjian Yuan, Dongjiao He, Bingyang Zhou, Zheng Liu, Jiarong Lin, Fangcheng Zhu, Yunfan Ren, Rong Wang, Fanle Meng, Fu Zhang
机构:University of Hong Kong、Information Science Academy of China Electronics Technology Group
原文链接:https://arxiv.org/abs/2408.14035
代码链接(代码已开源,开源日期:2025.1.23):https://github.com/hku-mars/FAST-LIVO2
1、摘要:
本文提出FAST-LIVO2:一种快速、直接的激光雷达-惯性-视觉里程计框架,实现准确同时定位和鲁棒状态估计测绘(SLAM)任务,并在实时机载机器人应用中提供了巨大的潜力。FAST-LIVO2融合IMU,激光雷达和图像测量,有效地通过一个错误状态迭代卡尔曼滤波(ESIKF)。为了解决这个维度针对异构激光雷达与图像测量不匹配的问题,在卡尔曼滤波中采用了顺序更新策略。为了提高效率,我们对两者都采用了直接方法视觉和激光雷达融合,其中激光雷达模块注册原始不提取点的边缘或平面特征和视觉效果模块最大限度地减少直接光度误差,无需提取ORB或FAST角落功能。视觉与视觉的融合激光雷达测量是基于单一的统一体素地图其中激光雷达模块构建几何结构为注册新的激光雷达扫描和视觉模块连接图像贴片到LiDAR点(即视觉地图点)启用新的图像对齐。提高图像的精度对准,我们使用平面先验的激光雷达点在体素地图(甚至在对齐之前细化平面处理),并在新图像对齐后动态更新参考补丁。进一步增强鲁棒性FAST-LIVO2采用了一种非要求的图像对齐方法光线投射操作和估计图像的曝光时间在现实中时间。我们在这两个基准上进行了大量的实验和私人数据集,证明我们提出的系统显著优于其他最先进的里程计系统在精度,鲁棒性和计算效率方面。此外,系统中关键模块的有效性也得到了验证。
2、我们的贡献:
FAST-LIVO2是在我们之前的工作中首次提出的FAST-LIVO基础上开发的[8]。与FAST-LIVO相比,新的贡献如下
- 我们提出了一个高效的ESIKF框架,采用顺序更新来解决激光雷达和视觉测量之间的尺寸不匹配问题,提高了使用异步更新的FAST-LIVO的鲁棒性。
- 我们使用(甚至改进)激光雷达点的平面先验来提高精度。相比之下,FAST-LIVO假设贴片中的所有像素共享相同的深度,这一大胆的假设大大降低了图像对齐中仿射翘曲的准确性。
- 为了提高图像对齐的精度,我们提出了一种参考补丁更新策略,通过选择高质量的、具有大视差和足够纹理细节的内层参考补丁。FAST-LIVO根据与当前视图的接近程度选择参考补丁,通常会导致低质量的参考补丁降低精度。
- 在线估计曝光时间,处理环境光照变化。FAST-LIVO没有解决这个问题,导致在明显的光照变化下图像对准的收敛性差。
- 我们提出了按需体素射线投射,以增强系统在激光雷达近距离盲区导致的没有激光雷达点测量的情况下的鲁棒性,这是FAST-LIVO中没有考虑的问题。
在综合消融研究中对上述每一项贡献进行了评估,以验证其有效性。我们将提出的系统作为实用的开放软件来实现,精心优化了在英特尔和ARM处理器上的实时运行。该系统是多功能的,支持多线旋转激光雷达,新兴的具有非常规扫描模式的固态激光雷达,以及针孔相机和各种鱼眼相机。
此外,我们在25个公共数据集序列(即Hilti和NTU-VIRAL数据集)以及各种具有代表性的私人数据集上进行了广泛的实验,以便与其他最先进的SLAM系统(例如R3LIVE, LVI-SAM, FAST-LIO2等)进行比较。定性和定量结果都表明,我们提出的系统在降低计算成本的情况下,在准确性和鲁棒性方面明显优于其他同行
3、系统框图
我们的系统概述如图2所示,其中包含四个部分:ESIKF(第IV节),局部测绘(第V节),激光雷达测量模型(第VI节)和视觉测量模型(第VII节)。
首先将异步采样的LiDAR点通过扫描重组重组为相机采样时间的扫描点。然后,我们通过ESIKF将激光雷达、图像和惯性测量紧密耦合、状态更新,其中系统状态依次更新,首先通过激光雷达测量,然后通过图像测量,两者都使用基于单个统一体素地图的直接方法(第IV节)。为了在ESIKF更新(第VI节)中构建激光雷达测量模型,我们计算帧到地图的点到平面残差。为了建立视觉测量模型(第七节),我们从地图中提取当前视场内的视觉地图点,利用可见体素查询和按需光线投射;提取后,我们识别并丢弃离群视觉地图点(例如,被遮挡或表现深度不连续的点);然后,我们计算帧到地图图像的光度误差进行视觉更新。
用于视觉和LiDAR更新的局部地图都是体素图结构(第V节):LiDAR点构建和更新地图的几何结构,而视觉图像将图像补丁附加到选定的地图点(即视觉地图点)并动态更新参考补丁。更新的参考补丁有他们的法向量进一步细化在一个单独的线程。

各部分更新已在后面标明注意查看
4、带顺序状态更新的错误状态迭代卡尔曼滤波器
本节概述了系统的架构,基于顺序更新的ESIKF框架。
4.1、符号和状态转换模型
在我们的系统中,我们假设三个传感器(LiDAR,IMU和相机)之间的时间偏移是已知的,可以提前校准或同步。我们将IMU框架(记为I)作为体框架,将第一个体框架作为全局框架(记为G)。此外,我们假设三个传感器是刚性连接的,表I中定义的外部传感器是预先校准的。然后,第i个IMU测量时的离散状态转换模型为:

其中Δt是IMU采样周期,状态x、输入u、过程噪声w和函数f定义如下:

其中GRI、GpI和GvI分别表示全局帧中的IMU姿态、位置和速度,Gg是全局帧中的重力矢量,τ是相对于第一帧的倒数相机曝光时间,nτ是将τ建模为随机游走的高斯噪声,ωm和am是原始IMU测量值,ng和na是ωm和am中的测量噪声,ba和bg是IMU偏差,其被建模为分别由高斯噪声nbg和nba驱动的随机游走。
算法流程图如下:

4.2、扫描复合(个人认为是重点)
我们采用扫描重组将高频、顺序采样的LiDAR原始点分割成相机采样时刻的不同LiDAR扫描,如图3所示。这确保相机和LiDAR数据以相同的频率同步(例如,10 Hz),允许同时更新状态。

在ESIKF框架中,状态和协方差从接收到最后一次LiDAR扫描和图像帧的时间tk-1传播到接收到当前LiDAR扫描和图像帧的时间tk。该前向传播通过将(1)中的过程噪声wi设置为零来预测tk-1和tk期间每个IMU输入ui处的状态。将传播状态表示为x,协方差表示为P,这将作为第IV-D节中后续更新的先验分布。
此外,为了补偿运动失真,我们进行了反向传播[42],确保在扫描结束时间tk“测量”LiDAR扫描中的点。注意,为了简化符号,我们省略了所有状态向量中的下标k。
4.3、顺序更新方法(误差状态迭代卡尔曼滤波器的算法框架)
IMU传播状态x的先验和协方差P的先验对时刻tk的系统状态x施加了一个先验分布,如下所示:

我们将上述先验分布表示为p(x),并将LiDAR和相机的测量模型表示为

其中vl ~ N (0, Σvl)和vc ~ N (0, Σvc)分别表示LiDAR和相机的测量噪声。
标准ESIKF[43]将使用所有当前测量值更新状态x,包括激光雷达测量值yl和图像测量值yc。然而,激光雷达和图像测量是两种不同的传感方式,其数据尺寸并不匹配。此外,图像测量的融合可以在图像金字塔的各个层次上进行。为了解决维度不匹配问题并为每个模块提供更大的灵活性,我们提出了一个顺序更新策略。该策略在理论上等同于使用所有测量值的标准更新,假设给定状态向量x的LiDAR测量值yl和图像测量值yc具有统计独立性(即,测量值被统计独立的噪声破坏)。
为了引入顺序更新,我们将当前状态x的总条件分布重写为:

上式表明,总条件分布p(x| y1,yc)可以通过两个连续的贝叶斯更新来获得。第一步仅将LiDAR测量值y1与IMU传播的先验分布p(x)进行融合,以获得分布p(x| yl)的值:

然后,第二步骤将相机测量yc与p(x)融合|yl),以获得x的最终后验分布:

有趣的是,联立以上两个融合遵循相同的形式::

为了对LiDAR或图像测量进行(8)中的融合,我们详细描述先验分布q(x)和测量模型q(y| x)如下。对于先验分布q(x),记为x = x <
δ
x
,其中
δ
x
<
δx,其中δx <
δx,其中δx<N(0,P)。在LiDAR更新的情况下(即,第一步),(x,P)是从传播步骤获得的状态和协方差。在视觉更新的情况下(即,第二步),(x,P)是从LiDAR更新获得的收敛状态和协方差。为了获得测量模型分布q(y| x),将第k次迭代时估计的状态表示为xκ,其中x0 = x。通过其在xκ处进行的一阶泰勒展开来近似测量模型(4)(LiDAR或相机测量)导致:

其中δxκ = x <
x
κ
,
z
κ
是残差,
L
κ
v
<
xκ,zκ是残差,Lκ v <
xκ,zκ是残差,Lκv<N(0,R)是集总测量噪声,Hκ和Lκ是h的雅可比矩阵(xκ ∈ δxκ,v)相对于δxκ和v,分别在零处求值。然后,代入先验分布q(x)和测量分布q(y| x)的后验分布(8)中并执行最大似然估计,我们可以从ESIKF框架中的标准更新步骤获得δxκ(以及xκ)的最大后验估计[43]:

然后,收敛状态和协方差矩阵使后验分布的均值和协方差为q(x|y)。
后续说明:
文献[44]和[45]研究了具有顺序更新的卡尔曼滤波器。本文采用这种方法用于LiDAR和相机系统的ESIKF。算法1中详细描述了具有顺序更新的ESIKF的实现。
在第一步(第6-10行)中,迭代地从LiDAR测量(参见第VI-A节)更新误差状态,直到收敛。收敛的状态和协方差估计,再次表示为x和P,用于更新地图的几何形状(见第V-B节),随后在第二步视觉更新(第13-23行)中对图像金字塔的每个级别进行细化(见第VII-B节),直到收敛。最优状态和协方差(表示为< x 和 P < x和P < x和P<)用于传播输入的IMU测量值(见第IV-C节)并更新地图的视觉结构(见第V-D节和V-E节)。
5、本地地图更新
5.1、地图的结构(voxelmap论文的引用)
我们的地图采用了[14]中提出的自适应体素结构,它由哈希表和每个哈希条目的八叉树组织(见图2)。哈希表管理根体素,每个体素具有0.5 × 0.5 × 0.5 m的固定尺寸。每个根体素封装八叉树结构,以进一步组织不同大小的叶体素。叶体素表示局部平面并存储平面特征(即,平面中心、法向矢量和不确定性)沿着与位于该平面上的一组LiDAR原始点。其中一些点与三级图像补丁(8 × 8补丁大小)相连,我们称之为视觉地图点。收敛的视觉地图点仅与参考补丁相连,而非收敛的则与参考补丁和其他可见补丁相连(见第V-E节)。叶体素的变化大小允许其表示不同尺度的局部平面,从而可适应具有不同结构的环境[14]。

为了防止地图的大小变得无限制,我们仅在LiDAR的当前位置周围的长度为L的大的局部区域内保持局部地图,如图4中的2-D示例所示。最初,该贴图是以LiDAR的起始位置p0为中心的立方体。LiDAR的检测区域将被可视化为以其当前位置为中心的球体,其半径由LiDAR的检测范围定义。当LiDAR移动到检测区域接触地图边界的新位置p1时,我们将地图从边界移动一段距离d,包含移出局部地图的区域的存储器将被重置,以存储在局部地图中移动的新区域。这种环形缓冲区方法确保了我们的局部映射保持在固定大小的内存中。[46]中详细介绍了环形缓冲区哈希映射的实现。在每个ESIKF更新步骤之后执行地图检查。

本地地图幻灯片二维演示。在(a)中,灰色矩形是长度为L的初始映射区域。红色圆圈是以p0为中心的初始检测区域。在(B)中,检测区域移动到地图边界被触摸的新位置p1。贴图区域将移动到新位置(蓝色矩形),移动距离为d。在(c)中,存储器空间B保持不变。在(B)中,对于蓝色区域C,对存储绿色区域的存储空间A进行复位。(a)初始地图。(b)移动地图。(c)重置存储器
5.2、几何构造与更新
地图的几何形状是由激光雷达点测量数据构建和更新的。具体来说,在ESIKF(第IV节)中的LiDAR更新之后,我们将LiDAR扫描的所有点注册到全局框架。对于每个注册的LiDAR点,我们在哈希图中确定其根体素的位置。如果体素不存在,我们用新点初始化体素,并将其索引到哈希图中。如果确定的体素已经存在于地图中,我们将点附加到现有的体素上。在一次扫描中所有的点都分布好之后,我们进行如下的几何构造和更新。
对于新创建的体素,我们根据奇异值分解来确定是否所有包含的点都在一个平面上。如果是,则计算该平面的中心点q = p¯,平面法向n,以及(q, n)的协方差矩阵Σn,q。Σn,q用来表征平面不确定度,平面不确定度是由位姿估计不确定度和点测量噪声引起的。详细的平面判据及平面参数和不确定度的计算可参考我们之前的工作[14]。如果包含的点不在一个平面上,则该体素将被连续细分为八个更小的八边形,直到子体素中的点被确定为形成一个平面或最大层。在后一种情况下,叶子体素中的点将被丢弃。因此,地图只包含识别为平面的体素(根或子)。
对于添加了新点的现有体素,我们评估新点是否仍然与根体素或子体素中的现有点形成一个平面。如果没有,我们按照上面的方法进行体素细分。如果是,我们更新平面的参数(q,n)和协方差Σn,q也如上所述。一旦平面参数收敛(见[14]),将为认为该平面上的成熟点和新点将被丢弃。成熟平面的估计平面参数(q,n)和协方差Σn,q是固定的。
平面上的LiDAR点(根体素或子体素)将用于在后续部分生成可视地图点。对于成熟的飞机,50个最新的LiDAR点作为视觉地图点生成的候选点,而对于不成熟的飞机,所有的LiDAR点都是候选点。视觉地图点生成过程将识别这些候选点中的一些作为视觉地图点,并将它们附加上图像补丁以进行图像对齐。
5.3、可视化地图点的生成和更新
为了生成和更新视觉地图点,我们在地图中选择候选LiDAR点,这些点(1)在当前帧中可见(详见第VII-A节),以及(2)在当前图像中显示出显著的灰度梯度。
在视觉更新(章节IV-D)之后,我们将这些候选点投影到当前图像上,并保留每个体素中局部平面深度最小的候选点。
然后,我们将当前图像划分为均匀的网格单元,每个单元为30 × 30像素。如果网格单元不包含投影在这里的任何视觉地图点,我们使用具有最高灰度梯度的候选点生成一个新的视觉地图点,并将其与当前图像补丁、估计的当前状态(即帧姿态和曝光时间)以及从上一节的LiDAR点计算的平面法线相关联。
附着在视觉地图点上的patch有三个相同大小的层(例如11×11像素),每一层都是前一层的一半采样,形成一个patch金字塔。如果一个网格单元包含投影在这里的视觉地图点,如果(1)自上次添加补丁以来已经过了20帧以上,或者(2)其当前帧中的像素位置偏离上次添加补丁时的位置超过40个像素,我们将向现有的视觉地图点添加新的补丁(所有三层金字塔)。因此,地图上的点可能会有均匀分布视角的有效补丁。
除了patch金字塔,我们还将估计的当前状态(即姿态和曝光时间)附加到地图点上。
5.4、参考补丁更新
由于添加了新补丁,一个可视地图点可能有多个补丁。我们需要在视觉更新中选择一个参考补丁进行图像对齐。我们根据光度相似度和视角对每个patch f进行评分如下:(本章节为理想化的模型主要是假设了光度不变性)

其中NCC(f, g)表示用于测量patch f和patch g,在两个patch的第0金字塔层(分辨率最高的层),对两个patch进行均值相减,c表示待评价patch f的法向量n与视点方向p/∥p∥之间的余弦相似度。
当patch正对着地图点所在平面时,c的值为1。总体得分S由加权的NCC和c相加计算,其中前者表示待评价patch f与所有其他patch gi之间的平均相似度,tr(Σn)表示法向量协方差矩阵的轨迹。
在所有附加到可视地图点上的补丁中,得分最高的补丁被更新为参考补丁。上述评分机制倾向于选择(1)外观与大多数其他补丁相似(就NCC而言)的参考补丁,这是MVS[47]使用的一种技术,以避免动态对象上的补丁;(2)视场方向与平面正交,以高分辨率保持纹理细节。相比之下,我们之前的工作FAST-LIVO[8]和现有技术[4]中的参考补丁更新策略直接选择与当前帧视图方向差异最小的补丁,导致所选参考补丁非常接近当前帧,因此对当前姿态更新的约束较弱。

图像说明:(a)参考面片和目标面片之间的仿射变形。(b)任何位于归一化球面上的法线Irn ∈ S2首先投影到平面Irp T M=1上的点M ∈ R3,然后投影到x-y平面上的点m ∈ R2。因此,该变换将球面上的扰动δn转换为x-y平面上的扰动δm。
5.5、法线细化
假设每个视觉地图点位于一个小的局部平面上。现有的工作[2],[4],[8]假设补丁中的所有像素具有相同的深度,这是一个通常不成立的狂野假设。我们使用从LiDAR点计算的平面参数,如第V-B节所述,以实现更高的精度。该平面法线对于在视觉更新过程中执行用于图像对准的仿射变形是至关重要的。为了进一步提高仿射变形的准确性,可以从附加到视觉地图点的面片进一步细化平面法线。具体来说,我们通过最小化相对于附加到视觉地图点的其他补丁的光度误差来细化参考补丁中的平面法线。
1)仿射翘曲:
仿射变形用于从参考帧变换块像素(即,源补片)以补片其余帧中的像素(即,设uj,r是源块中的第j个像素坐标,并且uj,i是第i个目标块中的第j个像素坐标。假设块中的所有像素位于具有法线Ir n和视觉地图点位置Ir p(其对应于源块和目标块两者的中心像素)的局部平面中,这两者都表示在源块帧中,我们有

其中Ai,r表示将像素坐标从源(或参考)区块变换到第i个目标区块的仿射扭曲矩阵,Ii,RIr和Ii,tIr表示参考帧Ir的相对姿态w.r. t。目标帧Ii。为了直接使用鱼眼图像而不将其校正为针孔图像,我们基于不同的相机模型(例如,P是针孔相机模型的相机固有矩阵)。
2) 法线优化:
为了细化平面法线Ir n,我们最小化参考块与第0金字塔层级处的其它图像块之间的光度误差(即,最高分辨率)

其中N是路径大小,τr和τi分别是参考帧和第i个目标帧的逆曝光时间。Ir(uj,r)表示参考帧中的第j块像素,Ii(Ai,ruj,r)表示第i目标帧中的第j路径像素,并且S是所有目标帧的集合。
3) 优化变量变换:
为了提高计算效率,我们重新参数化(14)中的最小二乘问题。注意,优化变量Ir n仅出现在(13)中的M <$ 1 IrnT·Irp Ir n ∈ R3中,可以对Ir n进行优化。此外,向量M受到约束Ir p · M=1,这意味着M可以如下参数化

其中Ir pz =0,因为没有这样的参考片可以被选择用于视觉映射点。图5(B)示出了Ir n、M和之间的关系。
最后,在向量m ∈ R2上进行(14)中的优化而没有任何约束。这种优化可以在单独的线程中执行,以避免阻塞主里程计线程。然后,优化的参数项可以用于恢复最佳法向量Ir n

一旦平面法线收敛,该视觉映射点的参考片和法线向量就被固定而无需进一步细化,并且所有其他片被删除。
6、激光雷达测量模型
6.1、点对平面激光雷达测量模型
在获得扫描中未失真的点{Lpj}后,我们使用激光雷达更新第κ次迭代时估计的状态x^κ将它们投影到全局帧:

然后我们识别根或子体素,其中G^p κ j在哈希图中。如果没有找到体素或体素不包含平面,则丢弃该点。否则,我们使用体素中的平面来建立LiDAR点的测量方程。具体来说,我们假设真实的LiDAR点Lp gt j,给定准确的LiDAR位姿GTI,应该在体素中有法线n gt j和中心点q gt j的平面上。也就是说,

由于地真点Lp gt j的测量值为Lpj,其中包含测距噪声和轴承噪声δ Lpj,因此我们得到Lp gt j = Lpj−δ Lpj。同样,平面参数(n gt j,q gt j)估计为(nj, qj),协方差为Σn,q(节V-B),因此我们有:n gt j = nj⊟δnj,q gt j = qj−δqj。因此,

其中测量噪声vl = (δ Lpj, δnj, δqj),分别由LiDAR点、法向量、平面中心相关噪声组成。
6.2、光束发散激光雷达测量噪声
在[14]中,局部LiDAR帧中LiDAR点δLpj的不确定性被分解为两个分量,由激光飞行时间(TOF)引起的测距不确定性δd和源自编码器的方位方向不确定性δω。除了这些不确定性之外,我们还考虑了由激光束发散角θ引起的不确定性,如图6所示。随着方位方向与法向量之间的角度θ的增加,LiDAR点的测距不确定性显著增加,而方位方向不确定性保持不受影响。由于激光束发散角引起的δd可以建模为:

考虑到δd受飞行时间和激光束发散的影响,当我们的系统从地面或墙壁上选择更多的点时[见图6(c)和(d)],它实现了比不考虑这种影响更精确的位姿估计。

(a)图(a)和(B)分别示出了考虑激光束发散角θ的LiDAR点不确定性模型的3D和侧截面图。红色轮廓线描绘了激光束传播的区域。©以及(d)通过点位置不确定性对扫描中的点着色。与(c)相比,(d)还考虑了由光束发散角引起的测距不确定性δd。由于激光束的大扩展区域,这导致地面点的更高不确定性。
7、目视测量模型
7.1、可视化地图点选择
为了在视觉更新中执行稀疏图像对齐,我们开始选择适当的视觉映射点。我们首先使用体素和光线投射查询提取当前相机FoV中可见的映射点集(称为视觉子映射)。然后,选择来自该子地图的视觉地图点,并拒绝离群值。该过程产生一组精细的视觉地图点,准备用于在视觉测量模型中构建视觉光度误差。
1)可见体素查询
识别当前帧FoV内的标测图体素具有挑战性,因为标测图中有大量体素。为了解决这个问题,我们轮询当前扫描中LiDAR点击中的体素。这可以通过使用测量点位置查询体素哈希表来有效地完成。如果相机FoV与LiDAR FoV大部分重叠,则相机FoV中的映射点也可能位于这些体素中。假设两个连续的图像帧具有大的FoV重叠,我们还轮询在前一图像帧中被识别为可见的图点(通过相同的体素查询和光线投射)命中的体素。最后,可以获得当前视觉子图作为这两种类型的体素中包含的图点,然后进行FoV检查。
2)点播广播构成(3D点映射到2D点的过程)
在大多数情况下,可视子地图可以通过上述体素查询获得。然而,当激光雷达传感器太靠近一个物体(称为近距离盲区)时,它可能无法返回任何点。此外,相机FoV可能不会完全被激光雷达FoV覆盖。为了在这些情况下回忆更多的可视地图点,我们采用了如图所示的光线投射策略。

如上图,我们将图像划分为均匀的网格单元,每个单元为30 × 30像素,并将从体素查询中获得的视觉地图点投影到网格单元上。对于每个没有被这些视觉地图点占用的图像网格单元,沿着中心像素向后投射一条光线,其中样本点沿深度方向从dmin到dmax均匀分布。为了减少计算量,在相机体帧中对每条光线上的采样点位置进行了预计算。对于每个采样点,我们评估相应体素的状态:如果体素包含投影后位于该网格单元中的地图点,我们将这些地图点合并到视觉子地图中,并停止此射线。否则,我们继续到射线上的下一个采样点,直到达到最大深度dmax。通过光线投射对所有未被占用的图像网格单元进行处理,得到一组分布在整个图像中的可视地图点。
3)异常画面排除:
经过体素查询和光线投射,我们获得了当前帧FoV中的所有可视地图点。然而,这些视觉地图点可能在当前帧中被遮挡,深度不连续,参考斑块在大视角下拍摄,或者在当前帧中具有大视角,这些都会严重降低图像对准精度。为了解决第一个问题,我们计划所有的使用LiDAR更新后的姿态将子地图中的可视地图点导入当前帧,并保持每个网格单元中30 × 30像素的最低深度点。为了解决第二个问题,我们将当前LiDAR扫描中的LiDAR点投影到当前帧中,生成深度图。通过将视觉地图点的深度与其在深度图中的9 × 9相邻点的深度进行比较,确定它们的遮挡和深度变化。遮挡和深度不连续的地图点被拒绝(见图8)。为了解决第三和第四个问题,我们删除了参考补丁或当前补丁的视角(即从可视地图点到补丁光学中心的法向量和方向之间的夹角)太大(例如超过80°)的点。剩余的可视地图点将用于对齐当前图像

异常值剔除。(a)显示了被遮挡的和深度不连续的可视标测图点的示意图。(b)显示了在真实的场景中剔除离群值的效果。红点是被拒绝的可视标测图点,绿色是被接受的可视标测图点。
7.2、稀疏-直接视觉测量模型–(SLAM直接法)
使用先前提取的视觉地图点{Gpi}来构建视觉测量模型。基本原理是,当将映射点Gpi变换为具有地面实况状态的当前图像Ik(·)时(即,pose)xk,则参考面片和当前面片之间的光度误差应该为零
视觉仿射翘曲为激光仿射翘曲反馈得到

其中π(·)是公共相机投影模型(即,针孔,MEI,ATAN,Scaramuzza,等距),Cr TG是全局框架Gw.r.t.参考帧Cr,其在接收和融合参考帧时已经被估计,Ar i是将像素从第i个当前块变换到参考块的仿射扭曲矩阵,Δu是到当前块内的中心ui的相对像素位置,Igtk、Igtr表示参考帧和当前帧的地面真实像素值,分别它们被测量为具有测量噪声vc =(δIk,δIr)的实际图像像素值Ik,Ir,其源自各种源[例如,散粒噪声和照相机CMOS的模数转换器(ADC)噪声]。因此:

为了提高计算效率,我们采用逆合成公式[4],[48],其中姿态增量δT ∈ R6参数化GTI =Gui中的Tκ I Exp(δT)[参见(21)],从ui移动到u i,如下所示:
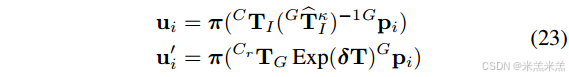
考虑到参考系中的u i在每次迭代期间保持不变,我们仅需要对雅可比矩阵w.r.t.δT,而不是每次迭代都重新计算它们。
为了从测量(22)估计逆曝光时间τk,我们固定初始逆曝光时间τ0 =1以消除当所有逆曝光时间为零时(22)的退化。因此,后续帧的估计的逆曝光时间是相对于第一帧的曝光时间。
等式(22)用于跨越三个级别的视觉更新步骤中(参见算法1);视觉更新从粗略级别开始,在一个级别的收敛之后,其前进到下一个更精细级别。然后使用估计的状态来生成视觉标测图点(参见第V-C节)并更新参考块(参见第V-D节)。
效果评估:





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










