bellman-ford算法、spfa算法求带负环的最短路、差分约束

一、bellman-ford算法、spfa算法求带负环的最短路

Ⅰ、引入背景

Q1：当图中含有负环的时候，为什么dijkstra算法会失效？

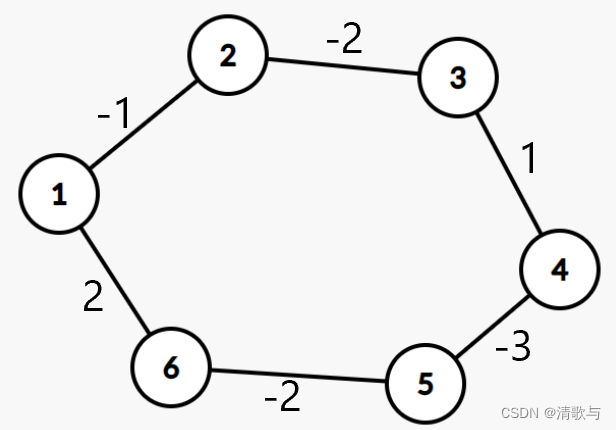
dijkstra算法:利用贪心思想，每次找最短的距离，在此基础上进行更新。

Q2：为什么bellman-ford和spfa能解决含有负环的最短路问题？
Q3：bellman-ford和spfa如何解决含有负环的最短路问题？

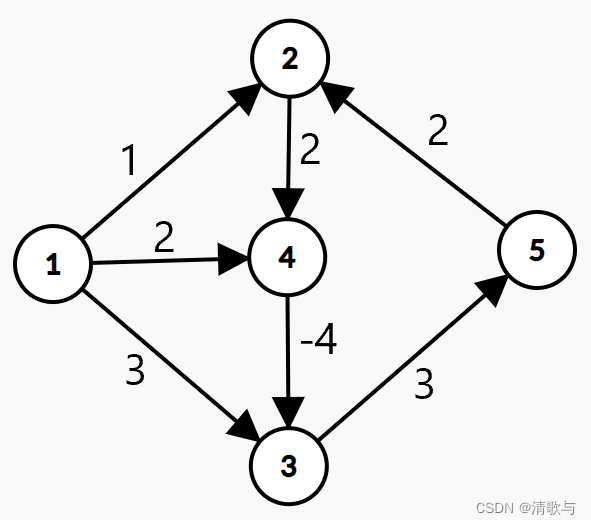
Ⅱ、bellman-ford算法求最短路代码实现

• Bellman-ford适用范围：单源最短路径（找给定源点到其他点的最短距离）、有边数限制的最短路问题，图中边的权重可为负数即负权边，但不可以出现负权环，可以判断负环。
• 时间复杂度是O(nm)。

const int N = 1e4 + 10;
const int inf = 0x3f3f3f3f;
int n, m, k;//点数，边数，可以使用的最大边数
int back1[N];//防止某个点的最短边更新两次
int dist[N];//标记从1-n的最短路径长度
struct node{
    int a,b,w;//起点，终点，权值
}e[N];

void bellman_ford(){
    memset(dist, inf, sizeof dist);
    dist[1] = 0;
    for(int i=1; i<=k; i++){
        memcpy(back1,dist,sizeof dist);
        for(int j=1;j<=m;j++){
            int x = e[j].a,y=e[j].b,z=e[j].w;
            dist[y] = min(dist[y],back1[x]+z);
        }
    }
    if(dist[n] > inf / 2) cout <<"impossible";
    else cout << dist[n];
}

Q4：为什么要引入back1数组？

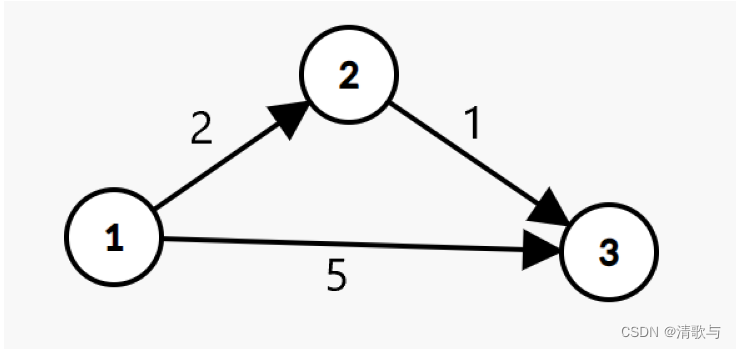
假设边数限制为1。

从1号点开始按边进行更新，首先e(1,2) -> dist[2]更新为2，其次e(1,3)->dist[3]更新为5,最后e(2,3) -> dist[3]更新为3。显然，不符合边数限制。

Ⅲ、SPFA（Shortest Path Faster Algorithm)算法求最短路代码实现

• spfa算法本质上是bellman-ford算法优化的一种方式，使用队列优化。
• spfa算法适用范围：和bellman-ford算法的适用范围一致，但是时间复杂度是一般O(m)， 最坏 O(nm）。

**应用一：spfa求最短路径**
const int N = 1e4 + 10;
int n, m, a, b, c;
int dist[N];//从1号点到i号点的最短距离
int cnt[N];//从1号点到i号点最短距离时的边数
int e[N], w[N], h[N], ne[N], idx;//建立邻接表
bool vis[N];//标记是否已经在队列中

void add(int a, int b, int c){
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

void spfa(){
    memset(dist, 0x3f, sizeof dist);
    queue<int> q;//存储下一次更新的点
    dist[1] = 0;
    q.push(1);
    vis[1] = true;
    while(!q.empty()){
        int t = q.front();
        q.pop();
        vis[t] = false;
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[t] + w[i]){
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n){
                    cout <<"-1" << endl;
                    return;
                }
                if(!vis[j]){
                    q.push(j); vis[j] = true;
                }
            }
        }
    }
    cout << dist[n];
}

**应用二：spfa判断图中是否存在负环**
//只需要再开一个cnt[]数组记录边数
const int N = 1e4 + 10;
int w[N], idx, h[N], e[N], ne[N];
int dist[N], cnt[N], n, m, x, y, z;
bool vis[N];

void add(int a, int b, int c){
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

void spfa(){
    queue<int> q;
    //判断图中是否存在负环时，要把每一个点作为最开始的点都遍历一遍。如果只将1号点放到队列中，
    //只是判断了以1为起点的路径，是否存在负环
    for(int i = 1; i <= n; i ++){
        q.push(i);
        vis[i] = true;
    }
    while(!q.empty()){
        int t = q.front();
        q.pop();
        vis[t] = false;
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[t] + w[i]){
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n){
                    cout <<"Yes";return;
                }
                if(!vis[j]){
                    q.push(j);
                    vis[j] = true;
                }
            }
        }
    }
    cout <<"No";
}

Ⅳ、相关题目：

1、p2136 拉近距离（基础最短路应用）

题意:n个点，m条有向边，问从点1到点n是否存在负环，存在负环输出“Forever love”，否则输出点1到点n的最短距离。

思路：单向边，边权为负值且可能存在负环，选择spfa算法。既要记录从初始点到终点的最短距离，也要判断是否含有负环。需要注意的是，小红也可以追小明，所以以小明为初始点走了一遍之后，还要以小红为初始点再走一遍。

题目代码：
#include<bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;
int n, m, a, b, c, minn1, ans = 0x3f3f3f3f;
int dist[N];//从起始点点到i号点的最短距离
int cnt[N];//从起始点到i号点最短距离时的边数
int e[N], w[N], h[N], ne[N], idx;//建立邻接表
bool vis[N];//标记队列中是否含有点i
int flag = 0;

void add(int a, int b, int c){
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

void spfa( int st){
    memset(cnt,0, sizeof cnt);//一定要记得初始化！！
    memset(dist, 0x3f, sizeof dist);
    queue<int> q;//存储下一次更新的点
    dist[st] = 0;//对起始点进行初始化
    q.push(st);
    vis[st] = true;
    while(!q.empty()){
        int t = q.front();
        q.pop();
        vis[t] = false;
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[t] + w[i]){
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if(cnt[j] >= n){
                    cout <<"Forever love" << endl;
                    flag = 1;//标记是否存在负环
                    return;
                }
                if(!vis[j]){
                    q.push(j); vis[j] = true;
                }
            }
        }
    }
    if(st == 1) minn1 = dist[n];
    else if(st == n) minn1 = dist[1];
}

int main(){
   memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        cin >> a >> b >> c;
        c = -c;//题目中说了，是减少c
        add(a, b , c);
    }
    spfa(1);
    if(flag == 1) return 0;
    //如果不存在负环，那么就需要从小明到小红走一遍，再从小红到小明走一遍，然后比较终点的最小值
    ans = min(minn1, ans);
    spfa(n);
    ans = min(minn1, ans);
    cout << ans << endl;
    return 0;
}

二、差分约束

Ⅰ、基本概念

1、差分约束背景引入

差分约束时一种特殊的$N$元一次不等式组，它包含$N$ 个变量$X_1$~$X_2$以及$M$个约束条件，每个约束条件都是由两个变量做差构成的，形如$X_i-X_j\le c_k$，其中$c_k$是常数。我们要解决的是，找到一组解$X_1=a_1,X_2=a_2,...,X_n=a_n$。

差分约束系统条件$X_i-X_j\le c_k$，可以变形为$X_i\ge c_k+X_j$。这与单源最短路中的三角形不等式$dist[y]\le dist[x]+z$非常相似。可以把每个变量$X_i$看作一个有向图的节点i，对于每一个约束条件$X_i\ge c_k+X_j$建一条有向边，一条从结点$j$指向结点$i$的长度为$c_k$的有向边。

2、差分约束注意点

• 差分约束系统要么无解，要么有无数组解。求不出最短路或最长路的时候是任意解。
• 对于a-b<=c,建边是b->a，长度为c的边，求最短路，若存在负环，则无解。
  对于a-b>=c,建边是b->a, 长度为c的边，求最长路，若存在正环，则无解。

Ⅱ、例题

1、差分约束算法（差分约束模板题）

题意：给出一组包含m个不等式，有n个未知数的形如：

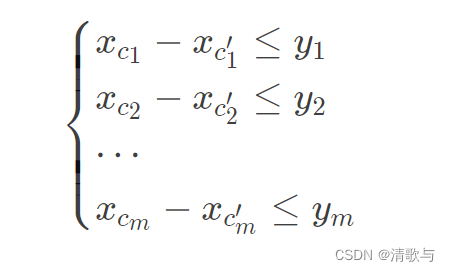
的不等式组，求任意满足这个不等式组的解。
输入：第一行为两个整数n，m，代表未知量的数量和不等式的数量。
接下来m行， 每行包含三个数c,c',y，代表一个不等式$x_c$ - $x$_c’$\le$ $y_m$。

AC代码

Q5：以哪一点为源点呢？
引入一个超级源点，源点到其他点的距离是零。

2、THE MATRIX PROBLEM（差分约束）

给一个$n\times m$的矩阵C，矩阵中每个元素都是不超过1000的正整数。问题是求解，是否存在n个数$a_1$,$a_2$,…,$a_n$和m个数$b_1$,$b_2$,…,$b_m$，满足$$L\le a[i]\times c[i][j]÷b[j]\le U$$

存在输出"YES"，不存在输出"NO"。

输入： 第一行给出: n, m, L, U
接下来n行，每行m个数表示矩阵C。

AC代码