Day01-02 | 第一章 数组part01-02

Day1任务

数组理论基础，704. 二分查找，27. 移除元素

704. 二分查找

704. 二分查找

看这个视频 掌握算法的本质思想：二分查找为什么总是写错？_哔哩哔哩_bilibili

【4.16补充】

究竟是 nums[mid] < target 还是 nums[mid] <= target? 怎么理解？

首先明确，写这个条件是干啥？是判断是否涂蓝色。OK。明确这一点后，我们的注意力应放在mid指针与target的关系上面。

假设target有好多个，例如下面图中的【5 5 5】。mid变来变去，假设此刻mid指到了【5 5 5】的任意一个元素上，下面代码要进行万众瞩目的if条件判断了：

情况一：若条件判断写了 nums[mid] < target

因为我们已假设mid指到了target，即nums[mid] == target，故与条件判断矛盾，条件判断不成立，target就不涂成蓝色（涂成红色）

对应图中上半部分的情况。

情况二：若条件判断写了 nums[mid] <= target

因为我们已假设mid指到了target，即nums[mid] == target，故与条件判断相符，条件判断成立，target会涂成蓝色

对应图中下半部分的情况。

【2.7补充】

二分无非就是下图这四种题型，我根据蓝红分界线的位置，用白线划分成了两组，也正好对应isBlue的符号，上面那组是<target，下面那组是<=target：

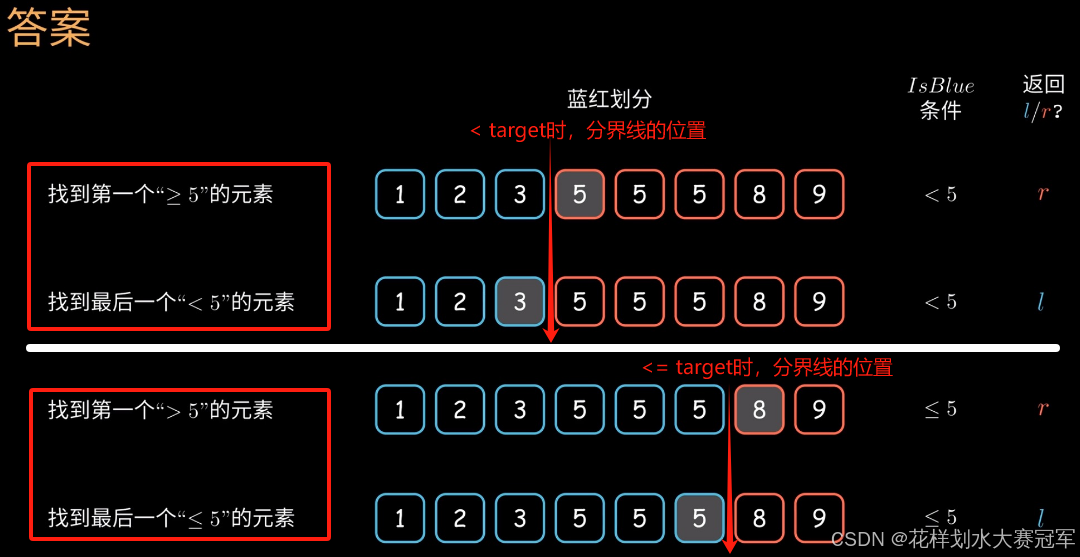
需要炉火纯青掌握二分算法，必须做到：看到题目，脑海中迅速浮现起相应的图形画面，即isBlue  < 时、 <= 时，蓝红分界线在哪里，是蓝还是红指针指向了我们想要的元素。

解题思路

1. 初始化l = -1, r = nums.length, 明确循环条件：l+1 != r
2. 循环结束时，l+1 == r，此时l是蓝区最后一个元素，r是红区第一个元素。
3. 返回到底是l还是r? 蓝区所有元素 <= target 返回 l（因为target在蓝区的末尾），蓝区 < target 返回 r（因为target在红区的首位）
4. 不要忘记后处理，检查 返回的指针所指元素是否为目标值 + 数组下标是否出现越界的情况 (如果指针是-1或者nums.length会出现越界异常)，如果检验通过，则说明能找到target；否则，返回-1

心得

• 通过与target比较，来缩小target所在的区间，是二分的本质。
• isBlue()中，到底是<=还是<的关键，在于最终形成的分界线在哪里，所谓分界线就是，数组已经全部涂成蓝/红，蓝红之间的界线，应当始终明确循环结束时，l+1 == r，蓝红界线形成
• 二分的使用前提：有序数组
• 二分的最大优势是在于其时间复杂度是O(logn)，因此看到有序数组要第一时间问自己是否可以用二分

写法1: num[mid] <= target涂成蓝色，返回蓝(左)指针

class Solution {
    // 判断mid位置的元素是否为“蓝色”
    private boolean isBlue(int[] nums, int mid, int target) {
        return nums[mid] <= target;
    }

    public int search(int[] nums, int target) {
        int l = -1, r = nums.length;
        // 找分界线
        while (l + 1 != r) {
            int m = l + (r - l) / 2;
            if (isBlue(nums, m, target)) {
                l = m;
            } else {
                r = m;
            }
        }

        // 分界线已明了。需要进行后处理，检查r指向的元素是否为目标值，如果是，则返回r；否则，返回-1
        if (l > -1 && nums[l] == target) {
            return l;
        } else {
            return -1;
        }
    }
}

写法2: num[mid] < target涂成蓝色，返回红(右)指针

class Solution {
    // 判断mid位置的元素是否为“蓝色”
    private boolean isBlue(int[] nums, int mid, int target) {
        return nums[mid] < target;
    }

    public int search(int[] nums, int target) {
        int l = -1, r = nums.length;
        // 找分界线
        while (l + 1 != r) {
            int m = l + (r - l) / 2;
            if (isBlue(nums, m, target)) {
                l = m;
            } else {
                r = m;
            }
        }

        // 分界线已明了。需要进行后处理，检查r指向的元素是否为目标值，如果是，则返回r；否则，返回-1
        if (r < nums.length && nums[r] == target) {
            return r;
        } else {
            return -1;
        }
    }
}

27. 移除元素

27. 移除元素 - 力扣（LeetCode）

「1.23补充」用快慢指针法 删除元素后得到的数组，还保留着原数组的顺序。所以，如果有保留原数组顺序的需求，还是优先用快慢指针法。

 快慢指针法（有保留原数组顺序的需求，优先选这个）

• 快指针：负责条件判断，寻找新数组的元素，即不需要移除的元素

• 慢指针：有规律地向右移动，存放新数组

• 注意，这里不同于相向双指针法，慢指针存放的是不需要移除的元素

class Solution {
    public int removeElement(int[] nums, int val) {
        int l = 0; // l为慢指针，r为快指针
        for(int r = 0; r < nums.length; r++){
            // 只要快指针发现正常的元素，就扔给慢指针
            if(nums[r] != val){
                nums[l] = nums[r];
                l++;
            } 
        }
        return l;
    }
}

 复习可以看下面的注释。考试的时候写上面👆的代码，简洁，写起来比较快。 

class Solution { 
    public int removeElement(int[] nums, int val) {
        int slowIndex = 0; // 慢指针，表示新数组的下标位置
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) { // 快指针遍历整个数组
            if (nums[fastIndex] != val) { 
                nums[slowIndex] = nums[fastIndex]; // 将不等于 val 的元素赋值到慢指针位置
                slowIndex++; // 慢指针向右移动
            }
        }
        return slowIndex; // 慢指针的最终位置就是新数组的长度
    }
}

解题思路（相向双指针法）

1. 初始化左右双指针，写循环体，明确条件：left <= right
2. 判断左指针处的值，如果需要移除（异常值），则用右指针的元素覆盖该元素 + 右指针左移
3. 反之，没有要移除的，则左指针右移

心得（相向双指针法）

• 左指针：判断是否需要移除 + 指向更新后的 新数组的Idx，左指针所到之处，皆为新元素
• 右指针：从右往左，发掘新元素，并且把该元素“传”给左指针
• 快慢指针的思想和相向指针类似，唯独就是条件判断和指针移动方向不一样，快慢指针是判断快指针的值是否非异常值，然后“传”给慢指针，两个指针都从左往右移动
• 时间复杂度为 O(n)

 相向双指针法

class Solution {
    public int removeElement(int[] nums, int val) {
        int n = nums.length;
        int l = 0, r = n - 1;
        for(; l <= r; l++){
            if(nums[l] == val){
                nums[l] = nums[r];
                r--;
                l--;
            } 
        }
        return l;
    }
}

👆上面的这个代码可读性差，复习/初学看下面的👇即可。 

class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0; // 左指针
        int right = nums.length - 1; // 右指针
        while (left <= right) {
            if (nums[left] == val) { // 左指针位置的值需要移除
                nums[left] = nums[right]; // 直接用右指针值覆盖
                right--; // 右指针左移
            } else {
                left++; // 左指针右移
            }
        }
        return left; // 左指针最终位置即为新数组长度
    }
}

 暴力法

class Solution {
    public int removeElement(int[] nums, int val) {
        // 暴力法:双层循环嵌套
        int n = nums.length;
        for (int i = 0; i < n; i++){
            if (nums[i] == val){
                // 从删除位置后每个元素左移
                for (int j = i + 1; j < n; j++) {
                    nums[j - 1] = nums[j];
                }
                i--; //这里容易出错，因为移动后i指针不动，需要从当前位置再检查
                n--;
            }
        }
        return n;
    }
}

977.有序数组的平方

977. 有序数组的平方 - 力扣（LeetCode）

【2.9补充】

一定是把较大的平方值 放到新数组的末尾，从新数组的末尾从后向前进行填充。

截至条件是 l <= r ，因为每个元素都要遍历到（如果<的话刚好差一个）。这样才是O(n)的复杂度

思路

相向双指针，从数组两端开始，比较平方的大小，较大的值 填入新数组的末尾。

心得

• 双指针法 时间复杂度为 O(nlogn)

• 初始化l = 0, r = nums.length - 1 时, while(l <= r)的执行次数等于数组nums.length

• Java 数组排序函数

  Arrays.sort(nums);

双指针法

class Solution {
    public int[] sortedSquares(int[] nums) {
        int l = 0;
        int r = nums.length - 1;
        // new一个新数组res，和原数组一样大，让k指向res数组终止位置。
        int[] res = new int[nums.length];
        int k = nums.length - 1;
        
        while(l <= r){
            if(nums[l] * nums[l] > nums[r] * nums[r]){
                res[k--] = nums[l] * nums[l];
                ++l;  //右移
            }else{
                res[k--] = nums[r] * nums[r];
                --r;  //左移
            }
        }
        return res;
    }
}

---

Day2任务

两道算法题：209.长度最小的子数组 59.螺旋矩阵II

编程思想：区间和  开发商购买土地

209.长度最小的子数组

209. 长度最小的子数组 - 力扣（LeetCode）

思路

• 定义滑动窗口：

  • 使用两个指针 left 和 right，分别表示当前窗口的左右边界。初始时，两个指针都指向数组的开头。
  • sum 记录当前窗口内元素的和，初始为 0。
  • result 用于存储满足条件的最小子数组长度，初始值为 Integer.MAX_VALUE。

• 扩展窗口：

  • 右指针 right 从左到右遍历数组，表示扩展当前窗口。每次将新元素 nums[right] 累加到 sum 上。

• 收缩窗口：

  • 不能一直扩展下去，所以要设置一个条件来收缩窗口
  • 当窗口和 sum >= s 时，移动左指针 left 来收缩窗口，寻找最小的窗口长度
  • 每次移动 left 缩小窗口前，要记录下 缩小前的 滑动窗口的长度（right - left + 1）
  • 缩小窗口：从 sum 中减去 nums[left]; left右移。

• 后处理，返回结果：

  • 如果 result 仍然为初始值 Integer.MAX_VALUE，表示没有找到符合条件的子数组，返回 0。
  • 否则返回 result。

心得

• Integer.MAX_VALUE 无限大的一个整数值

• 滑动窗口的本质：满足了单调性，即左右指针只会往一个方向走且不会回头。

• 收缩的本质：去掉不再需要的元素。也就是本题我们可以先固定移动右指针，判断条件是否可以收缩左指针算范围。

• 新加入滑动窗口的元素有负数怎么办？这样就不能用滑动窗口了，因为有负数的话无论你收缩还是扩张窗口，你里面的值的总和都可能增加或减少，就不像之前收缩一定变小，扩张一定变大，一切就变得不可控了。如果要 cover 所有的情况，那每次 left 都要缩到 right，那就退化为暴力了哈哈。

• 在滑动窗口DEBUG的小技巧？一般是怀疑哪里有问题就打印哪里 像今天的滑动窗口 就可以把窗口首尾的下标变化过程打印出来 能很清楚的看到窗口是怎样移动的

• 双指针和滑动窗口有什么联系？滑动窗口实际上是双层遍历的优化版本，而双指针其实只有一层遍历，只不过是从头尾开始遍历的。

• 滑动窗口的原理？窗口右端先开始走，然后直到窗口内值的总和 >= target，此时就开始缩圈，缩圈是为了找到最小值，只要此时总和还 >= target，就一直缩小，缩小到< target为止。在这过程中不断更新最小的长度值，然后右边继续走，如此反复，直到右边碰到边界。这样就保证了可以考虑到最小的情况

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // 初始化滑动窗口参数
        int l = 0;
        int sum = 0;
        int res = Integer.MAX_VALUE;  // 子数组的长度

        // 右指针从数组起点开始，一步步右移，不断扩大窗口
        for (int r = 0; r < nums.length; r++){
            sum += nums[r]; // 将新加入窗口的元素 不断累加起来
            // 窗口不能一直扩大下去，必须设置一个“度”，当违背了这个“度”时（sum >= target），需要缩小窗口
            while (sum >= target){
                // 记录缩小前的滑动窗口的长度，r - l + 1
                res = Math.min(res, r - l + 1);
                // 缩小窗口，减去左端元素的值，然后左指针右移（下面2个语句顺序不能颠倒）
                sum -= nums[l];
                l++;
            }
        }
        
        // 后处理检验：如果 res 还是初始定义的最大值，说明没有找到符合条件的子数组
        return res == Integer.MAX_VALUE ? 0 : res; // 双目运算符的写法
        // 对双目运算符不熟悉，也可以用下面的写法：
        // if(res == Integer.MAX_VALUE){
        //     return 0;
        // }
        // return res;
    }
}

59.螺旋矩阵II

59. 螺旋矩阵 II - 力扣（LeetCode）

思路

【2.26二刷】【3.27三刷】

参考灵神的思路：

59. 螺旋矩阵 II - 力扣（LeetCode）

附代码：

class Solution {
    // DIRS是4x2的矩阵，表示「右下左上」4个前进方向，对应顺时针螺旋的顺序。
    // 不同的行表示不同的前进方向，不同的列 表示 行与列的增量。
    private static final int[][] DIRS = {{0, 1},    // 向右（行不变，列+1）
                                        {1, 0},     // 向下（行+1，列不变）
                                        {0, -1},    // 向左（行不变，列-1）
                                        {-1, 0}};   // 向上（行-1，列不变）

    public int[][] generateMatrix(int n) {
        int[][] ans = new int[n][n]; // 结果数组
        int i = 0, j = 0; // 第i行，第j列
        int di = 0; // DIRS数组的行索引，表示前进方向，初始为0，即：开始时的前进方向是「向右」。
        for (int val = 1; val <= n * n; val++) { // 遍历要填入的数，从1到n^2
            ans[i][j] = val;  // 将 当前要填入的数 填到 结果数组ans[i][j] 中
            int x = i + DIRS[di][0]; // 更新行号。DIRS[di][0]表示在当前方向下（di不变），行号（即 i）的增量。因此，x存储的是更新后的行号。
            int y = j + DIRS[di][1]; // 更新列号。DIRS[di][0]表示在当前方向下（di不变），列号（即 j）的增量。因此，y存储的是更新后的列号。
            // 如果 (x, y) 出界 或者 已经填入数字，说明当前方向已走到头，需要转向
            if (x < 0 || x > n-1 || y < 0 || y > n-1 || ans[x][y] != 0) {
                di = (di + 1) % 4; // 右转 90°（这里为什么 % 4？因为di的取值范围是0-3，表示四个方向）
            }
            i = i + DIRS[di][0]; // 更新行号(走一步)
            j = j + DIRS[di][1]; // 更新列号(走一步)
        }
        return ans;
    }
}

心得

• 关于offset的理解：offset的意义在于 结束一圈后 起始位置向后移 结束位置向前移。可以画和n=4的矩阵，会比较好理解。offset就是由于要去更向内的一圈，内圈元素更少的地方循环，所以循环的次数变少了
• 循环< n - offset 的含义：因为左闭右开，每次外循环遍历的并不是完整的一行/一列，要减去offset个元素
• 以上行的外循环为例：
• 

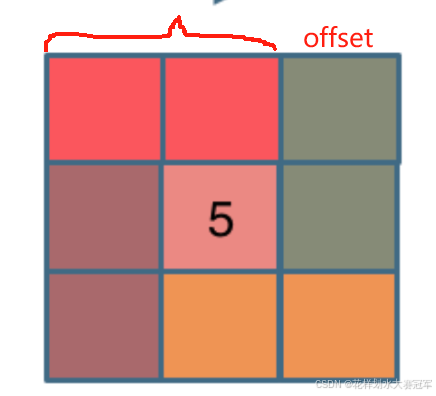
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        int startX = 0, startY = 0;  // 定义每循环一个圈的起始位置（每循环一个圈的左上角坐标）
        int offset = 1;  // 控制每一条边遍历的长度，左闭右开，每条边遍历不考虑最后一个数组元素
        int count = 1;   // 给矩阵中每个空格赋值，从1开始，每填充一个空格后++，直到填满整个nxn矩阵
        int i, j;        // 第 i 行; 第 j 列
        // 圈的填充
        // loop记录当前的圈数，例如n为奇数5，那么loop=2会循环2圈
        for(int loop = 1; loop <= n / 2; loop++){
            // 下面开始的四个for就是模拟转了一圈
            // 上行，从左到右，循环结束的条件是：遍历完一个长度为 n-offset 的边
            for (j = startY; j < n - offset; j++) {
                nums[startX][j] = count++;
            }
            // 此时j的位置是上面 左闭右开后没有遍历到 的位置

            // 右列，从上到下
            for (i = startX; i < n - offset; i++) {
                nums[i][j] = count++;
            }
            // 此时i的位置是右边 上闭下开后没有遍历到 的位置

            // 下行，从右到左，循环结束的条件是：j != startY
            for (; j > startY; j--) {
                nums[i][j] = count++;
            }

            // 左列，从下到上，循环结束的条件是：i != startX
            for (; i > startX; i--) {
                nums[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1，如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startX++;
            startY++;
            // offset 控制每一圈里每一条边遍历的长度
            offset++;
        }


        if (n % 2 == 1) { // n 为奇数时，单独处理矩阵中心的值
            nums[startX][startY] = count;
        }
        return nums;
    }
}

58. 区间和

58. 区间和（第九期模拟笔试）

心得(这个题得多刷，深刻掌握思想，牢记下图！)

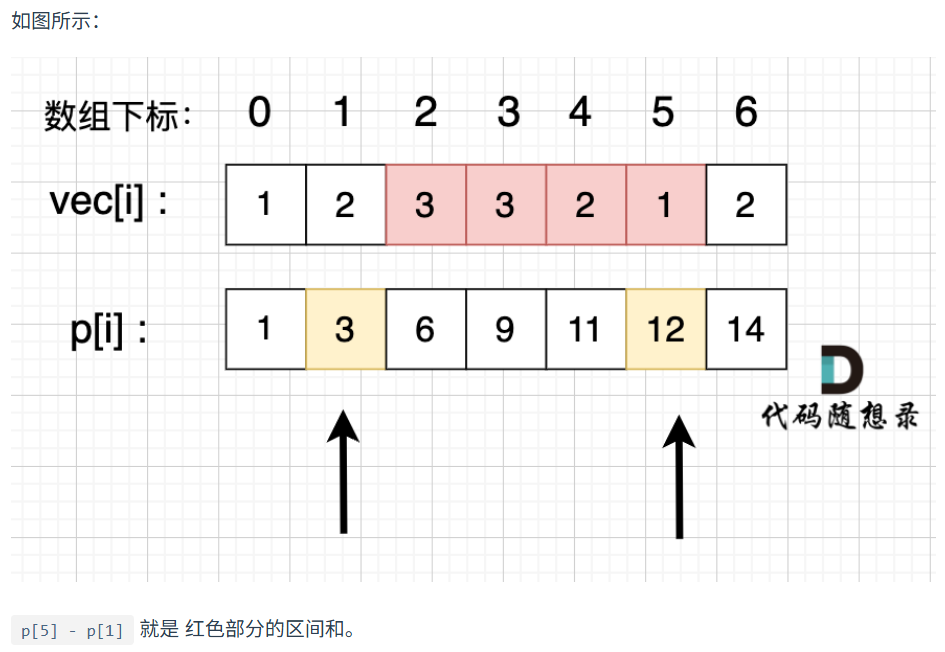
【2.26心得】这道题是用来学习 前缀和 思想 + 练习ACM模式的。

import java.util.Scanner;
 
public class Main {
    public static void main(String[] args) {
        // 创建 Scanner 对象用于读取输入
        Scanner scanner = new Scanner(System.in);
 
        // 读取数组的长度
        int n = scanner.nextInt();
        
        // 创建两个数组：nums 用于存储原始数组，p 用于存储前缀和数组
        int[] nums = new int[n];
        int[] p = new int[n];
 
        // 用于存储当前的前缀和
        int presum = 0;
        
        // 读取原始数组并计算前缀和
        for (int i = 0; i < n; i++) {
            nums[i] = scanner.nextInt();  // 读取数组元素
            presum += nums[i];            // 累加当前元素，更新前缀和
            p[i] = presum;                // 将当前的前缀和保存到 p 数组
        }
 
        // 循环读取查询区间，直到文件结束
        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();  // 读取区间的起始位置
            int b = scanner.nextInt();  // 读取区间的结束位置
 
            int sum;  // 用于存储当前查询区间的和
            if (a == 0) {
                // 如果起始位置为 0，直接返回前缀和 p[b]
                sum = p[b];
            } else {
                // 否则，通过 p[b] - p[a - 1] 计算区间 [a, b] 的和
                sum = p[b] - p[a - 1];
            }
            // 输出当前区间的和
            System.out.println(sum);
        }
 
        // 关闭 Scanner，释放资源
        scanner.close();
    }
}

44. 开发商购买土地

44. 开发商购买土地（第五期模拟笔试）

心得

上一题的扩展题型。也是用到【前缀和】的思想。

数组总结