题解：2022年暑假ACM热身练习2

好久没写题解了，自从天梯赛以后敲代码就很少了，院赛手也是很生，这一次就当做是找找状态，有些题还是有点难度的，或者说有点坑（感觉有些题放3个月前还对我不是问题。。。太久没做题题感直接下来了），分享一下下：

J - 改革春风吹满地

题目描述
“ 改革春风吹满地,
不会AC没关系;
实在不行回老家，
还有一亩三分地。
谢谢!（乐队奏乐）”

话说部分学生心态极好，每天就知道游戏，这次考试如此简单的题目，也是云里雾里，而且，还竟然来这么几句打油诗。
好呀，老师的责任就是帮你解决问题，既然想种田，那就分你一块。
这块田位于浙江省温州市苍南县灵溪镇林家铺子村，多边形形状的一块地，原本是linle 的，现在就准备送给你了。不过，任何事情都没有那么简单，你必须首先告诉我这块地到底有多少面积，如果回答正确才能真正得到这块地。
发愁了吧？就是要让你知道，种地也是需要AC知识的！以后还是好好练吧…

输入
输入数据包含多个测试实例，每个测试实例占一行，每行的开始是一个整数n(3<=n<=100)，它表示多边形的边数（当然也是顶点数），然后是按照逆时针顺序给出的n个顶点的坐标（x1, y1, x2, y2… xn, yn）,为了简化问题，这里的所有坐标都用整数表示。
输入数据中所有的整数都在32位整数范围内，n=0表示数据的结束，不做处理。

输出
对于每个测试实例，请输出对应的多边形面积，结果精确到小数点后一位小数。
每个实例的输出占一行。

输入样例
3 0 0 1 0 0 1
4 1 0 0 1 -1 0 0 -1
0

输出样例
0.5
2.0

分析

这道题，一开始就想着是求多个三角形面积叠加即可，开始没看见是按着逆时针顺序输入点进去的，所以一直在思考咋确定每个底边，那样麻烦多了。看到这个条件以后我想大家都会想着用结构体数组去按顺序存储，赛后看题解是构造了结构体数组来存储每个点的坐标，但是我存储的是每条边，都可以。
但是这题有点坑，两种求三角形的方法都给卡了精度，首先都得求出来中心点的坐标（所有x和y都分别叠加后除以点数即可）：
（1）底高，这个方法的高用的是点到线的距离公式。wa了。
（2）1/2absinC，这里自作聪明以为输入的肯定是个正n边形，C直接置为2π/n，这个自然也会wa
这里的底*高会wa我猜是因为精度问题，毕竟涉及到了根号。
最好的，也就是最不丢失精度的就是利用两个矢量的叉乘，随便找到一个参照点（输入的某个点），然后任意两个相邻点和其构成的两个矢量叉乘实际上就可以得出两条边构成的三角形的面积的2倍

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
#define PI 3.141592653589793
struct Edge{
    int x1,y1,x2,y2;
}edge[105];
int main(){
    int n,x,y,x1,y1,x2,y2;
    while(~scanf("%d",&n)&&n){
        int pos=0;
        double s=0;
        for(int i=0;i<n;++i){
            scanf("%d%d",&x2,&y2);
            if(!i)x1=x2,y1=y2;
            else edge[pos++]={x1,y1,x2,y2},x1=x2,y1=y2;
        }
        x=edge[0].x1,y=edge[0].y1;
        for(int i=1;i<pos;++i){
            x1=edge[i].x1,x2=edge[i].x2,y1=edge[i].y1,y2=edge[i].y2;
            s+=1.0*(x*y1-x*y2-x1*y+x2*y+x1*y2-x2*y1)/2;
        }
        printf("%.1lf\n",s);
    }
}

标注
这题wa了5次。。。菜

Q - 一只小蜜蜂

题目描述
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。

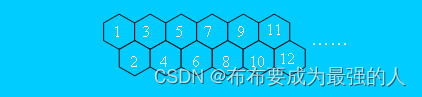
输入
输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。

输出
对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

输入样例
2
1 2
3 6

输出样例
1
3

分析

这题如果要问我到达n有几个步骤，那就是一个类似走楼梯的问题了，直接f[n]=f[n-1]+f[n-2]就好了。
这题我又犯傻了，一开始我还以为从m到n的路径数，就是从起点到n的路径数减去从起点到m的路径数。。。这真的是蠢到姥姥家了，f[50]-f[49]的答案肯定不是从49到50的路径数。。。
真实的就是f[n-m]，其实很容易，告诫大家还是要刷点题保持热度

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll step[55];
void solve(){
    step[1]=1,step[2]=2;
    for(int i=3;i<=50;++i)
        step[i]=step[i-1]+step[i-2];
}
int main(){
    int n;cin>>n;
    solve();
    while(n--){
        ll a,b;
        scanf("%lld%lld",&a,&b);
        printf("%lld\n",step[b-a]);
    }
}

备注
wa了我2次

R - 不容易系列之(3)―― LELE的RPG难题

题目描述
人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉，这可急坏了众多“Cole”（LELE的粉丝,即"可乐"）,经过多方打探，某资深Cole终于知道了原因，原来，LELE最近研究起了著名的RPG难题:

有排成一行的ｎ个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.

以上就是著名的RPG难题.

如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?

输入
输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成，(0<n<=50)。

输出
对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。

输入样例
1
2

输出样例
3
6

分析

一个思维比较简单的dp题，掉坑掉在没看到“首尾不能相同颜色”这句话，看到就好办了：
对于到第n个方块的情况数dp[n]，分为两种情况：（1）第n-1个方块和第一个方块的颜色不一样，那么第n个方块的选择只有1种，dp[n-1]；（2）第n-1个方块和第一个方块的颜色是一样的，那么只需要看前n-2的方块的选择种类即可，且我们的第n个方块的选择有2种，因为不能和n-1个方块颜色一样且不能和首部颜色一样，2dp[n-2]
综上dp[n]=dp[n-1]+2dp[n-2]

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll dp[55];
void solve(){
    dp[1]=3,dp[2]=6,dp[3]=6;
    for(int i=4;i<=50;++i)
        dp[i]=dp[i-1]+dp[i-2]*2;
}
int main(){
    ll n;
    solve();
    while(~scanf("%lld",&n)){
        printf("%lld\n",dp[n]);
    }
}

备注
wa我3次

S - 骨牌铺方格

题目描述
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

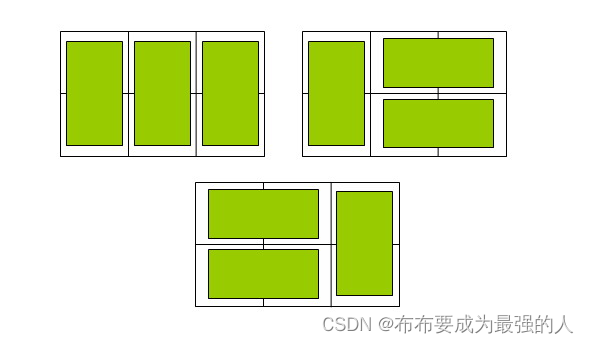
输入
输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

输出
对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

输入样例
1
3
2

输出样例
1
3
2

上一题把热度找回来了一些，这题感觉就挺容易的了，直接列出递推方程。对于整数n，铺放方案的总数为f[n]，显然是可以思考为第n列是竖下来的一列，那么情况就是f[n-1]，还有就是横着放两列，那么显然是f[n-2]，且正好容易发现f[n-1]+f[n-2]刚好把所有情况包揽进来了，且不包含重复的情况。因此这道题的状态方程就是f[n]=f[n-1]+f[n-2]
再举几个类似的例子，把题目变换一下，思维都是一样的，读者可以自己去体会一下：
（1）把题目描述中的2×n改为3×n：f[i]=f[i-1]+f[i-3]
（2）请在1×n的一个长方形方格中,任选1×1、1×2和1×3的骨牌铺满方格, 输入n,输出铺放方案的总数：f[i]=f[i-1]+f[i-2]+f[i-3]

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll dp[55];
void solve(){
    dp[1]=1,dp[2]=2;
    for(int i=3;i<=50;++i)
        dp[i]=dp[i-1]+dp[i-2];
}
int main(){
    ll n;
    solve();
    while(~scanf("%lld",&n)){
        printf("%lld\n",dp[n]);
    }
}

T - 阿牛的EOF牛肉串

题目描述
今年的ACM暑期集训队一共有18人，分为6支队伍。其中有一个叫做EOF的队伍，由04级的阿牛、XC以及05级的COY组成。在共同的集训生活中，大家建立了深厚的友谊，阿牛准备做点什么来纪念这段激情燃烧的岁月，想了一想，阿牛从家里拿来了一块上等的牛肉干，准备在上面刻下一个长度为n的只由"E" “O” "F"三种字符组成的字符串（可以只有其中一种或两种字符，但绝对不能有其他字符）,阿牛同时禁止在串中出现O相邻的情况，他认为，"OO"看起来就像发怒的眼睛，效果不好。

你，NEW ACMer,EOF的崇拜者，能帮阿牛算一下一共有多少种满足要求的不同的字符串吗？

PS: 阿牛还有一个小秘密，就是准备把这个刻有 EOF的牛肉干，作为神秘礼物献给杭电五十周年校庆，可以想象，当校长接过这块牛肉干的时候该有多高兴！这里，请允许我代表杭电的ACMer向阿牛表示感谢！

再次感谢！

输入
输入数据包含多个测试实例,每个测试实例占一行,由一个整数n组成，(0<n<40)。

输出
对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。

输入样例
1
2

输出样例
3
8

分析
这种题可以先列几个试试看

接着我们对f[4]的情况可以直接看出来，我想到的是所有f[3]的情况3，但是由于部分情况的末尾已经是O，乘以3显然不现实，那么我就要减去一些不应该有的情况，也就是减去f[3]中末尾带O的情况，观察就可以得知，f[3]中末尾会带O的，在f[2]的末尾必然不带O，且是一对一的关系（即f[2]中的某个末尾不带O的组合，产生的f[3]的组合中只会有一个末尾带O的情况），但是f[2]中会有多少种不带O的情况呢？直接看不带O的情况明显就没那么容易。因为再观察，就可以看出f[1]中的每个情况都必然会使得f[2]的组合会有两个末尾不带O的情况（一对二的关系），按着这个顺序就可以知道，多出来的情况就是2f[1]。
推得最后的状态方程f[i]=3f[i-1]-2f[i-3]

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll dp[40];
void solve(){
    dp[0]=1,dp[1]=3,dp[2]=8;
    for(int i=3;i<40;++i)
        dp[i]=3*dp[i-1]-2*dp[i-3];
}
int main(){
    int n;
    solve();
    while(~scanf("%d",&n)){
        printf("%lld\n",dp[n]);
    }
}

U - 神、上帝以及老天爷

题目描述
HDU 2006’10 ACM contest的颁奖晚会隆重开始了！
为了活跃气氛，组织者举行了一个别开生面、奖品丰厚的抽奖活动，这个活动的具体要求是这样的：

首先，所有参加晚会的人员都将一张写有自己名字的字条放入抽奖箱中；
然后，待所有字条加入完毕，每人从箱中取一个字条；
最后，如果取得的字条上写的就是自己的名字，那么“恭喜你，中奖了！”

大家可以想象一下当时的气氛之热烈，毕竟中奖者的奖品是大家梦寐以求的Twins签名照呀！不过，正如所有试图设计的喜剧往往以悲剧结尾，这次抽奖活动最后竟然没有一个人中奖！

我的神、上帝以及老天爷呀，怎么会这样呢？

不过，先不要激动，现在问题来了，你能计算一下发生这种情况的概率吗？

不会算？难道你也想以悲剧结尾？！

输入
输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(1<n<=20),表示参加抽奖的人数。

输出
对于每个测试实例，请输出发生这种情况的百分比，每个实例的输出占一行, 结果保留两位小数(四舍五入)，具体格式请参照sample output。

输入样例
1
2

输出样例
50.00%

这道题一拿到就想着是那种排列组合的问题，实际上是一种经典错排问题，但是我觉得一时半会挺难敲的，用dp的思维思考一下，可以这么想：假设n个人错排的可能数为f[n]，如果第n个人抽不到第n个，共有n-1种抽法，比如这个人抽第k个，那么接下来就有两种情况：第一种是第k个人抽到了第n个，那么剩下n-2个人，方法有f[n-2]种，如果第k个人没有抽到第n个，那么剩下共有f[n-1]种抽法。综上，f[n]=(n-1)*(f[n-1]+f[n-2])

第二种思考方式是我更喜欢的，这一切源于自己的思维定势，但是最好两者都理解，拓宽思维：
（1）假设第n个人开始抽纸条，如果已知前n-1个人都实现了错排，那么第n个人只需要和前面n-1个人互换就好，有n-1种互换的方案，然后两者互换完，剩下的n-2个人进行错排即可，即(n-1)*f[n-2]
（2）假设前n-1个人有个人抽到了第n个人的纸条，这有n-1个人可能抽到第n个人的纸条，那么除了这个人以外，还剩下n-1个人进行错排，得到(n-1)*f[n-1]

接下来只需要错排情况数/总情况数即可求出概率

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll f[25];
void solve(){
    f[2]=1,f[3]=2;
    for(int i=4;i<=20;++i)f[i]=(i-1)*(f[i-1]+f[i-2]);
}
int main(){
    int c,n;cin>>c;
    solve();
    while(c--){
        scanf("%d",&n);
        ll s=1;
        for(int i=2;i<=n;++i)s*=i;
        printf("%.2lf%%\n",1.0*f[n]/s*100);
    }
}

V - 不容易系列之(4)――考新郎

题目描述
国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体的操作是这样的:

首先,给每位新娘打扮得几乎一模一样,并盖上大大的红盖头随机坐成一排;
然后,让各位新郎寻找自己的新娘.每人只准找一个,并且不允许多人找一个.
最后,揭开盖头,如果找错了对象就要当众跪搓衣板…

看来做新郎也不是容易的事情…

假设一共有N对新婚夫妇,其中有M个新郎找错了新娘,求发生这种情况一共有多少种可能.

输入
输入数据的第一行是一个整数C,表示测试实例的个数，然后是C行数据，每行包含两个整数N和M(1<M<=N<=20)。

输出
对于每个测试实例，请输出一共有多少种发生这种情况的可能，每个实例的输出占一行。

输入样例
2
2 2
3 2

输出样例
1
3

这题和上一题就有类似的地方了，都是需要用到错排公式：f[n]=(n-1)*(f[n-1]+f[n-2])，但是不一样的地方是这题是有m个人选错了娘子，那么总共就要先在n个人中选取m个人，得出可能错排的人的情况，接着再乘以f[m]即可。
错排公式同上，而组合公式C(n,m)的计算，可以用我们最常用的公式即A(n,m)/A(m,m)=n*(n-1)*(n-2)*…*(n-m+1)/m*(m-1)*…*1=n!/(m!*(n-m)!)，写个循环还挺快的，但是我自己用的是另外一个公式，顺便分享一下：
C(n,m)=C(n-1,m-1)+C(n-1,m)
这个正好符合了递推的dp，还是挺好理解的：想要在n个里面挑m个，要不然就是在前n-1里面已经挑选了m-1个，接下来第n个默认被挑选；要不然就是前n-1个里面已经选了m个，第n个默认不被挑选。

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll f[25],s[25][25];
void solve(){
    f[2]=1,f[3]=2;
    for(int i=4;i<=20;++i)f[i]=(i-1)*(f[i-1]+f[i-2]);
    s[1][1]=1,s[1][0]=1;
    for(int i=2;i<=20;++i)
        for(int j=0;j<=20;++j)
            if(j==0)s[i][j]=1;
            else if(j>i)s[i][j]=0;
            else if(j==i)s[i][j]=1;
            else s[i][j]=s[i-1][j-1]+s[i-1][j];
}
int main(){
    int c,n,m;cin>>c;
    solve();
    while(c--){
        scanf("%d%d",&n,&m);
        printf("%lld\n",f[m]*s[n][m]);
    }
}

W - 折线分割平面

题目描述
我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

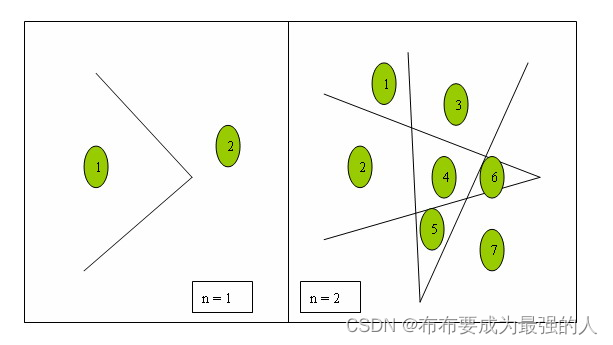
输入
输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

输出
对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

输入样例
2
1
2

输出样例
2
7

方法一：

建议大家看看这位大佬的博客，我觉得这种类比的思维是值得引起我们思考的：

折线分割|动态规划

方法二：直接类比欧拉公式
欧拉公式的内容：在平面上增加一条直线，增加的平面区数=该直线经过的直线数+1，为什么是这样呢？我的理解是把直线当成和所有其他直线的交点构成的线段+两条射线，每两个交点都会使得产生一个平面，两条射线分别分割一个平面，也就是欧拉公式理解为：
在平面上增加一条直线，增加的平面区数=交点数-1+2
那么交点数又可以最多是多少呢？理解欧拉公式以后我们就可以大胆做变换
可以直接把折线当成是两条射线，每条射线使得欧拉公式变为增加的平面区数=交点数-1+1=交点数，两条射线，那就乘以2就好了。
而可以产生最多的交点数，就能实现最多的平面数了，第 n 条折线的两边必须要和前 n-1 条折线的两边（共计 2(n-1) 条射线）相交。则新增射线 2 条，新增线段 4(n-1) 条。
然而新增的两条射线，源点都是一样的，得出推导方程：
f[n]=f[n-1]+4(n-1)+2-1=f[n-1]+4n-3，我们可以直接写这个公式提前打表，也可以把这个公式做可连续推导的一次性公式
f[n]=f[n-1]+4(n-1)+1
=f[n-2]+4(n-2)+4(n-1)+2
=…
=f[1]+4(1+2+3+…+n-1)+n-1
=2n^2-n+1

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
    int c,n;cin>>c;
    while(c--){
        scanf("%d",&n);
        printf("%d\n",2*n*n-n+1);
    }
}