红黑树- 插入、删除 流程详解，末尾附完整代码，及高清过程图

红黑树

红黑树是平衡二叉树的一种, 它与完全二叉树相比, 拥有更高效的插入和删除的效率, 还有能媲美完全二叉树的查找效率。

红黑树是由2-3树改进的一种数据结构，红黑树中的所有节点都被赋予一种颜色，要么黑色，要么红色; 因为有红色节点的存在，使得红黑树可以在进行插入、删除的操作的时候进行局部、少量的调整，即可维持红黑树的平衡。

调整操作包括：

1. 左旋 2. 右旋 3. 变色

红黑树的性质

性质1：每个节点要么是黑色，要么是红色。

性质2： 根节点是黑色。

性质3：每个叶子节点是黑色。

性质4： 每个红色节点的两个自节点一定都是黑色，不能有两个红色节点相连。

性质5： 任意一节点到每个叶子节点的路径都包含数量相同的黑节点，称为黑高。

红黑树的这些性质保证了：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长，因而保证了红黑树是大致平衡的。因为树的查找、添加、删除操作都与树的高度成正比，所以红黑树的这些性质保证了，红黑树在最差的情况下，仍有很好的查找，添加 和删除的效率。

红黑树保持自平衡的操作

1.变色

在必要的情况下，对节点进行变色处理，以维护红黑树的性质。

2.左旋

左旋操作是平衡树高的操作之一，对节点进行左旋操作可以使原节点位置的左子树高度减一，右子树的高度加一。

 /**
 *          p                      p     
 *          |                      |     
 *          n                      y     
 *        /  \      --->         /  \ 
 *       x    y                 n    ry   
 *           / \              /  \       
 *         ly   ry           x   ly     
 * 左旋操作
 * 1. 将y的左子节点ly连接到n右子节点上
 * 2. 修改ly的父节点指向n
 * 3. 将n连接到y的左子节点位置上
 * 4. 修改n的parent指定y
 * 5. 修改y的parent指向n的父节点
 * 6. 修改p本指向n的子节点指向y
 * @param node
 */
private void leftSpin(Node<K,V> node){
    if(node!=null){
        Node<K,V> rn=node.right;
        Node<K,V> pn=node.parent;
        if(rn!=null){
            //将y的左子节点ly连接到n右子节点上
            node.right=rn.left;
            //修改ly的父节点指向n
            if(rn.left!=null)
                rn.left.parent=node;
            //将n连接到y的左子节点位置上
            rn.left=node;
            //修改n的parent指定y
            node.parent=rn;
            if(pn!=null){
                //修改y的parent指向n的父节点
                rn.parent=pn;
                //修改p本指向n的子节点指向y
                if(pn.left==node){
                    pn.left=rn;
                }else {
                    pn.right=rn;
                }
            }else {
                rn.parent=null;
                this.root=rn;
            }

        }



    }

}

3.右旋

对节点进行右旋操作可以使原节点位置的右子树高度减一，左子树的高度加一。

/**
 *           p                  p
 *           |                  |
 *           n                  x
 *         /  \               /  \
 *        x    y  --->      lx    n
 *      /  \                     / \
 *    lx   rx                  rx   y
 *
 *
 * 右旋操作
 * 1. 将x的右子节点rx连接到n左子节点上
 * 2. 修改rx的父节点指向n
 * 3. 将n连接到x的右子节点位置上
 * 4. 修改n的parent指定x
 * 5. 修改x的parent指向n的父节点
 * 6. 修改p本指向n的子节点指向x
 * @param node
 */
private void rightSpin(Node<K,V> node){
    if(node!=null){
        Node<K,V> ln=node.left;
        Node<K,V> pn=node.parent;

        if(ln!=null){
            //将x的右子节点rx连接到n左子节点上
            node.left=ln.right;
            //修改rx的父节点指向n
            if(ln.right!=null)
                ln.right.parent=node;
            // 将n连接到x的右子节点位置上
            ln.right=node;
            // 修改n的parent指定x
            node.parent=ln;

            if(pn!=null){
                // 修改x的parent指向n的父节点
                ln.parent=pn;
                // 修改p本指向n的子节点指向x
                if(pn.left==node){
                    pn.left=ln;
                }else {
                    pn.right=ln;
                }
            }else{
                ln.parent=null;
                this.root=ln;
            }
        }


    }
}

插入节点

插入节点，前三种情况都比较简单，只有第四种情况需要调整

1.根节点为空

​ 直接将node设为根节点，并设置为黑色。

2.插入节点的key值已存在

​ 直接更新当前节点的值为新节点的值

3. 父节点为黑色

​ 直接插入红色节点，不影响树平衡。

4. 父节点为红色（父亲节点必定为黑色，性质4）

4.1 叔叔节点为红色

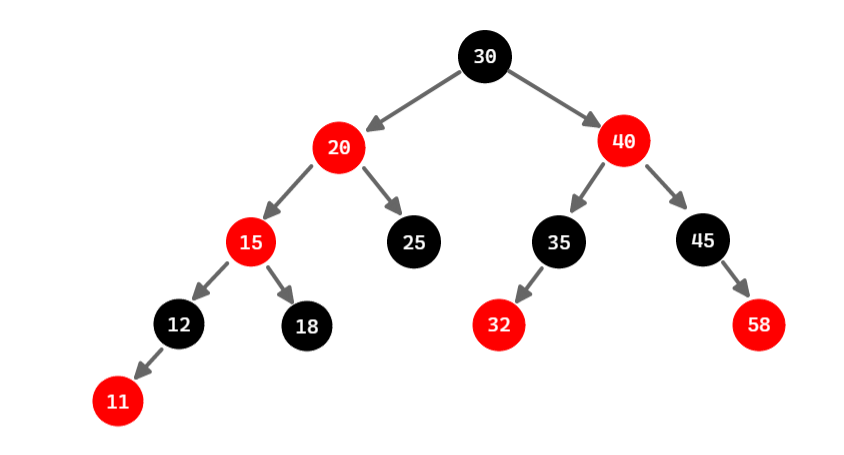
例如：插入节点 11

被插入节点和父亲节点红红相连，违反了性质4

这种情况下，以被插入节点的爷爷节点为根节点的子树范围内，无法通过左旋、右旋、变色操作来保持该子树的黑高不变，就需要向上扩大调整范围。

调整方法： 将父亲节点和叔叔节点染黑。爷爷节点染红。然后把爷爷节点15当成被插入的节点进行修复。

4.2 叔叔结点为黑色或为空

4.2.1 父节点在爷爷节点左侧，子节点在父节点左侧（LL双红）

例如插入31

出现了红红相连的情况，违反了性质4

调整方法：将父亲节点染黑。爷爷节点染红。 对爷爷节点右旋。

4.2.2 父节点在爷爷节点左侧，子节点在父节点右侧（LR双红）

这种情况与4.2.1的情况类似，可以很轻易的转换成4.2.1的情况

调整方法：对父亲节点左旋

就能转变成其他情况

4.2.3 父节点在爷爷节点右侧，子节点在父节点右侧（RR双红）

调整方法：将父亲节点染黑。爷爷节点染红。对爷爷节点左旋。

4.2.4 父节点在爷爷节点右侧，子节点在父节点左侧（RL双红）

调整方法：对父亲节点右旋 就转换成了4.2.3的情况

上述各种情况中 情况2 在插入元素时（putVal(Node<K,V> node)中）处理，其他情况都在fixTree(Node<K,V> node)中处理

插入元素

public void putVal(K key,V value){
    // 将key 和 value 封装成Node对象
    Node<K,V> node= new Node<K, V>(key, value);
    // 存入红黑树
    putVal(node);

}

private void putVal(Node<K,V> node){
    Node<K,V> temp=this.root;
    Node<K,V> parent=null;
    //找要插入元素的父节点
    while(temp!=null){
        parent=temp;
        int cmp=temp.key.compareTo(node.key);
        if(cmp>0){
            temp=temp.left;
        }else if(cmp==0){// 这种情况下，key值已经在集合中存在了，直接用新值替换旧值。
            temp.value=node.value;
            return;
        }else{
            temp=temp.right;
        }
    }

    //插入元素
    if(parent==null){
        this.root=node;
    }else if(parent.key.compareTo(node.key)>0){
        parent.left=node;
        node.parent=parent;
    }else{
        parent.right=node;
        node.parent=parent;
    }
    // 调用修复红黑树方法。
    fixTree(node);

}

修复红黑树

public void fixTree(Node<K,V> node){
    // 如果当前节点是黑色，说明这已经是处理过的、合格的红黑树子树了。
    if(!node.isRed()){
        return;
        }
    //1. 如果node是根节点，直接染为黑色
    if(node.parent==null){
        setBlack(node);
        return;
    }
    //父节点
    Node<K,V> parent=node.parent;
    //2. 如果父节点是黑色，就不需要处理，直接插入即可

    /*
      3. 如果父节点是红色，因为插入的节点是红色，红红不能相连，就需要处理
      3.1. 叔叔节点为红色
            将父亲节点和叔叔节点染黑。爷爷节点染红。
      3.2. 叔叔结点为黑色或为空
         3.2.1. 父节点在爷爷节点左侧，子节点在父节点左侧（LL双红）
                将父亲节点染黑。爷爷节点染红。对爷爷节点右旋。
         3.2.2. 父节点在爷爷节点左侧，子节点在父节点右侧（LR双红）
                对父亲节点左旋 然后转-->3.2.1.
         3.2.3. 父节点在爷爷节点右侧，子节点在父节点右侧（RR双红）
                将父亲节点染黑。爷爷节点染红。对爷爷节点左旋。
         3.2.4. 父节点在爷爷节点右侧，子节点在父节点左侧（RL双红）、
                对父亲节点右旋 然后转-->3.2.3.
     */
    if(isRed(parent)){
        //祖父节点
        Node<K,V> grandParent=parent.parent;
        //叔叔节点
        Node<K,V> uncle=null;
        //寻找叔叔节点
        if(grandParent.left==parent){
            uncle=grandParent.right;
        }else{
            uncle=grandParent.left;
        }

        //3.1 叔叔结点是红色
        if(uncle!=null && isRed(uncle)){
            setBlack(parent);
            setBlack(uncle);
            setRed(grandParent);
            fixTree(grandParent);
            return;
        }else{
            //3.2 叔叔节点是黑色或为空

            //3.2.1 和 3.2.2 父亲节点是祖父节点的左孩子
            if(parent==grandParent.left){
                //3.2.2 当前节点是父节点的右孩子
                if(node==parent.right){
                    // 对当前节点的父亲节点进行左旋操作，就能转变成了其他情况。
                    leftSpin(parent);
                    // 更改当前节点。
                    fixTree(node.left);
                    return;
                }else{//3.2.1 当前节点是父节点的左孩子
                    setBlack(parent);
                    setRed(grandParent);
                    // 对祖父节点右旋
                    rightSpin(grandParent);
                    //更改当前节点
                    fixTree(parent);
                    return;
                }


            }else {//父亲节点是祖父节点的右孩子
                //3.2.4 当前节点是父节点的左孩子
                if(node==parent.left){
                    // 对当前节点的父亲节点进行右旋操作，此时情况节就转变为3.2.3了。
                    rightSpin(parent);
                    // 更改当前节点。
                    fixTree(node.right);
                    return;
                }else{//3.2.4 当前节点是父节点的右孩子
                    setBlack(parent);
                    setRed(grandParent);
                    // 对祖父节点左旋
                    leftSpin(grandParent);
                    //更改当前节点
                    fixTree(parent);
                    return;
                }
            }
        }
    }

}

删除节点

删除节点的流程

1. 如果被删除节点是叶子节点，可以直接删除。
2. 如果删除节点是非叶子节点，那么需要找到他的前驱或后继节点，来替换掉被删除节点的键和值，再删除他的前驱或后继节点。

public Node<K,V> deleteNode(Node<K,V> node){
    Node<K,V> p=node.parent;
    // 如果是叶子节点，可以直接删除
    if(node.left==null && node.right==null){
        //  若被删除节点是红色，可以直接删除，如果是黑色，直接删除会影响黑高，所以要对红黑树进行修复处理
        if(!node.red)
            fixDelete(node);
        if(p==null) root=null;  //被删除节点是根节点的话，说明root没有子节点，直接将root置空即可
        else{
            //否则就正常地删除，
            node.parent=null;
            if(p.left==node){
                p.left=null;
            }else {
                p.right=null;
            }
        }
    }else{  // 如果被删除节点不是叶子节点，就找到node的前驱/后继节点，交换node与前驱/后继节点的值，再删除前驱/后继节点
        Node<K,V> e=getSuccessor(node);
        // 交换被删除节点与继承者节点的键
        K tempKey=e.key;
        e.key=node.key;
        node.key=tempKey;
        // 交换被删除节点与继承者节点的值
        V tempVal=e.value;
        e.value=node.value;
        node.value=tempVal;
        //删除被继承节点
        deleteNode(e);

    }

    return node;

}
//获取node的前驱或后继节点
Node<K,V> getSuccessor(Node<K,V> node){
    Node<K,V> e;
    //前驱节点： 左子树中，最靠右的叶子节点
    //后继节点： 右子树中，最靠左的叶子节点
    //若左子树不为空，开始寻找node的前驱节点
    if(node.left!=null){
        e=node.left;
        //寻找左子树中最靠右的节点。
        while(e.right!=null){
            e=e.right;
        }
    }else{//若左子树为空，开始寻找node的后继节点节点
        e=node.right;
        //寻找右子树中最靠左的节点
        while(e.left!=null) {
            e = e.left;
        }
    }
    return e;
}

修复删除后的红黑树

1.被删除节点是红色

这种情况不影响红黑树的性质，可以直接删除

2.被删除节点是黑色

2.1. 兄弟节点是黑色，且兄弟节点有红色的子节点

2.1.1. 兄弟节点的左子节点是红色

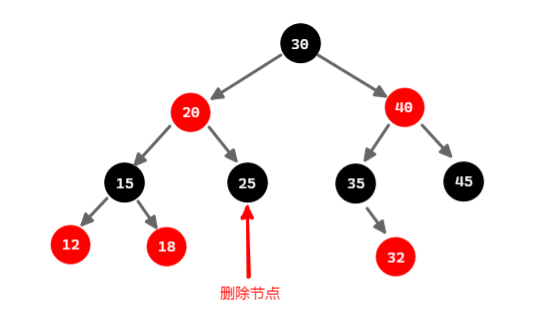
​ 此时父亲节点的右子树为空，左子树为ll（兄弟节点在父亲节点的左侧，兄弟节点的左子节点在兄弟节点的左侧 left-left），

调整方法：将兄弟节点的颜色染为原来父亲节点的颜色，再将兄弟节点的左子节点和父亲节点染为黑色， 再对父亲节点右旋。

​ 这样此子树的黑高就与删除前的黑高相等，此子树与删除前的子树相比，少了一个红色节点。

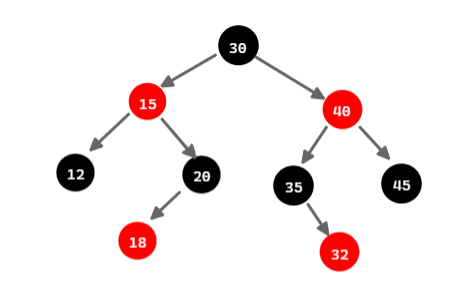
2.1.2. 兄弟节点的右子节点是红色

​ 此时父亲节点的右子树为空，左子树为lR（left-right）

对兄弟节点进行左旋，并交换兄弟节点与兄弟节点的右子节点的颜色，

就可转换为2.1.1 的情况

2.2.兄弟节点是黑色，且兄弟节点的子节点都为黑色。

这里要特别说明，空节点也是黑色节点

2.2.1. 父节点是红色

​

​ 将父亲节点染为黑色，兄弟节点染为红色即可

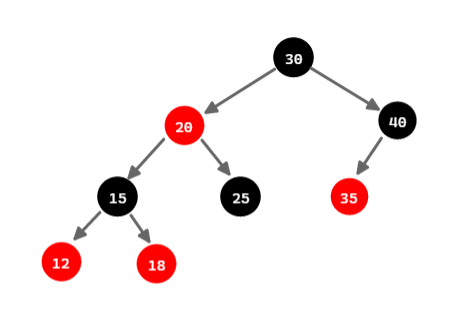
2.2.2. 父节点是黑色

​ 这种情况下，被删除节点、父亲节点、和兄弟节点都是黑色，被删除节点被删除后，不能在以父节点为根节点的子树范围内，保持黑高不变，此子树黑高必须减一，再扩大调整的范围，向上继续修复红黑树。

​ 具体操作为：将兄弟节点染为红色（以父节点为根节点的子树黑高减一），再以父亲节点为删除节点，修复红黑树。

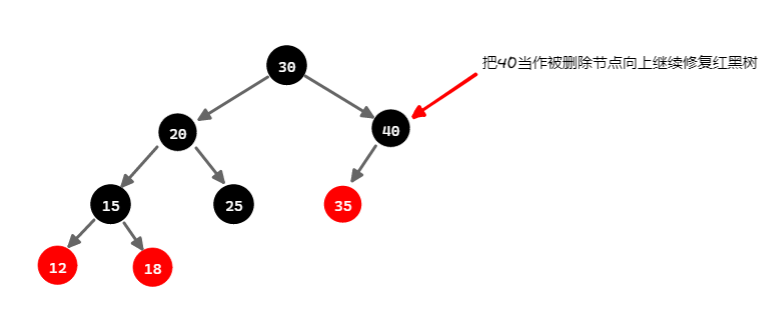
2.3. 兄弟节点是红色

父节点必定为黑色（性质4），且必定有黑色子节点，否则黑高不平衡（性质5）

父亲节点染为红色，兄弟节点染为黑色，再对父亲节点右旋，

此时就转换成了2.2.1的情况

public void fixDelete(Node<K,V> node){
    //记录下父节点
    Node<K,V> parent=node.parent;
    //兄弟节点
    Node<K,V> bro=null;

    if(parent==null){
        node.red=false;
        return;
    }
    // 如果被删除节点是父节点的右子树
    if(node==parent.right){
        // 那么兄弟节点就是父节点的左子节点
        bro=parent.left;

        // 2. 被删除节点是黑色
        if(isBlack(bro)){
            if(isRed(bro.left)){//   2.1.1. 兄弟节点的左子节点是红色
                bro.red=parent.red; //兄弟节点的颜色设为与父亲节点相同
                bro.left.red=false; //兄弟节点的左子节点染为黑色。
                parent.red=false;   //将父亲节点染为黑色。
                rightSpin(parent);  //对父亲节点右旋，

            }else if(isRed(bro.right)){    //  2.1.2. 兄弟节点的右子节点是红色
                bro.red=true;  // 将兄弟节点与兄弟节点的右子节点交换颜色。
                bro.right.red=false;
                leftSpin(bro);    // 再对兄弟节点左旋,情况就转换成了2.1.1
                fixDelete(node);  // 再次调用fixDelete（）方法，处理2.1.1的情况
                return;

            }else {  //  2.2.兄弟节点是黑色，且兄弟节点的子节点都是黑色
                //2.2.1. 父节点是红色
                if(parent.red){
                    parent.red=false;   //这种情况下并不影响黑高，这样处理只是模拟2-3树的处理方式，将父亲节点下沉
                    bro.red=true;

                }else{//    2.2.2. 父节点是黑色
                    bro.red=true;   //将兄弟节点染为红色后，以parent节点为根节点的子树黑高减一，此时需要扩大调整范围，以保证红黑树黑高平衡
                    fixDelete(parent);  //以父节点为被删除节点，调整子树。
                }
            }


        }else{//    2.3. 兄弟节点是红色
            parent.red=true;    //父亲节点染为红色。
            bro.red=false;      //兄弟节点染为黑色
            rightSpin(parent);  //右旋父亲节点，就转变成了2.2.1的情况
            fixDelete(node);    //再次调用fixDelete()函数，修复2.2.1的情况

        }

    }else{

        bro=parent.right;

        if(isBlack(bro)){

            if(isRed(bro.right)){
                bro.red=parent.red;
                bro.right.red=false;
                parent.red=false;
                leftSpin(parent);

            }else if(isRed(bro.left)){
                bro.red=true;
                bro.left.red=false;
                rightSpin(bro);
                fixDelete(node);
                return;

            }else {


                if(parent.red){
                    parent.red=false;
                    bro.red=true;

                }else{
                    bro.red=true;
                    fixDelete(parent);
                }
            }


        }else{
            parent.red=true;
            bro.red=false;
            leftSpin(parent);
            fixDelete(node);

        }

    }


}

完整代码

RBTree

//package src.top.goodbye.test.MapTest;

/**
 * 红黑树的性质
 * 1）每个结点要么是红的，要么是黑的。
 * 2）根结点一定是是黑的。
 * 3）所有叶子结点（叶子结点即指树尾端NIL指针或NULL结点）一定是黑的。
 * 4）如果一个结点是红的，那么它的俩个子结点一定都是黑的。
 * 5）从任一结点出发，到叶子结点的每一条路径，都包含相同数目的黑结点。
 *
 */
public class RBTree<K extends Comparable<K>,V> {
    private Node<K,V> root;

    static class Node<K extends Comparable<K>,V>{
        private Node<K,V> parent;
        private Node<K,V> left;
        private Node<K,V> right;
        private K key;
        private V value;
        // 红黑树默认结点是红色，因为加红色节点不会影响黑高。
        private boolean red = true;

        public Node() {
        }

        public Node(Node<K,V> parent, K key, V value) {
            this.parent = parent;
            this.key = key;
            this.value = value;
        }

        public Node(Node<K,V> parent, K key, V value, boolean red) {
            this.parent = parent;
            this.key = key;
            this.value = value;
            this.red = red;
        }


        public Node(K key, V value) {
            this.key=key;
            this.value=value;
        }

        public Node<K, V> getParent() {
            return parent;
        }

        public Node<K, V> getLeft() {
            return left;
        }

        public Node<K, V> getRight() {
            return right;
        }

        public K getKey() {
            return key;
        }

        public V getValue() {
            return value;
        }

        public boolean isRed() {
            return red;
        }
    }
    static class NullNodeException extends Exception {
        public NullNodeException() {
            super("空结点异常");
        }
    }

    public Node<K, V> getRoot() {
        return root;
    }

    //-------------------------辅助方法-----------------------------//
    /**
     * isRed(node); isBlack(node); setRed(node); setBlack(node); parentOf(node); inOrderPrint();
     */

    public boolean isRed(Node<K,V> node){
        if(node!=null)
            return node.red;
        return false;

    }
    public boolean isBlack(Node<K,V> node){
        if(node!=null)
            return !node.red;
        return true;

    }

    public void setRed(Node<K,V> node){
        if(node!=null)
            node.red=true;
    }

    public void setBlack(Node<K,V> node){
        if(node!=null)
            node.red=false;
    }

    public Node<K,V> parentOf(Node<K,V> node){
        if(node!=null && node.parent!=null)
            return node.parent;
        return null;
    }

    public void inOrderPrint(Node<K,V> node){
        if(node !=null){
            inOrderPrint(node.left);
            System.out.println("key:"+node.key +" value:"+node.value+" "+(node.red==true?"R":"B")+"\t");
            inOrderPrint(node.right);
        }
    }

    public void inOrderPrint(){
        inOrderPrint(root);
    }

    //----------------------------左旋，右旋-----------------------------//

    /**
     *          p                      p
     *          |                      |
     *          n                      y
     *        /  \      --->         /  \
     *       x    y                 n    ry
     *           / \              /  \
     *         ly   ry           x   ly
     * 左旋操作
     * 1. 将y的左子节点ly连接到n右子节点上
     * 2. 修改ly的父节点指向n
     * 3. 将n连接到y的左子节点位置上
     * 4. 修改n的parent指定y
     * 5. 修改y的parent指向n的父节点
     * 6. 修改p本指向n的子节点指向y
     * @param node
     */
    private void leftSpin(Node<K,V> node){
        if(node!=null){
            Node<K,V> rn=node.right;
            Node<K,V> pn=node.parent;
            if(rn!=null){
                //将y的左子节点ly连接到n右子节点上
                node.right=rn.left;
                //修改ly的父节点指向n
                if(rn.left!=null)
                    rn.left.parent=node;
                //将n连接到y的左子节点位置上
                rn.left=node;
                //修改n的parent指定y
                node.parent=rn;
                if(pn!=null){
                    //修改y的parent指向n的父节点
                    rn.parent=pn;
                    //修改p本指向n的子节点指向y
                    if(pn.left==node){
                        pn.left=rn;
                    }else {
                        pn.right=rn;
                    }
                }else {
                    rn.parent=null;
                    this.root=rn;
                }

            }



        }

    }
    /**
     *          p                  p
     *          |                  |
     *          n                  x
     *        /  \               /  \
     *       x    y  --->      lx    n
     *     /  \                     / \
     *   lx   rx                  rx   y
     *
     *
     * 右旋操作
     * 1. 将x的右子节点rx连接到n左子节点上
     * 2. 修改rx的父节点指向n
     * 3. 将n连接到x的右子节点位置上
     * 4. 修改n的parent指定x
     * 5. 修改x的parent指向n的父节点
     * 6. 修改p本指向n的子节点指向x
     * @param node
     */
    private void rightSpin(Node<K,V> node){
        if(node!=null){
            Node<K,V> ln=node.left;
            Node<K,V> pn=node.parent;

            if(ln!=null){
                //将x的右子节点rx连接到n左子节点上
                node.left=ln.right;
                //修改rx的父节点指向n
                if(ln.right!=null)
                    ln.right.parent=node;
                // 将n连接到x的右子节点位置上
                ln.right=node;
                // 修改n的parent指定x
                node.parent=ln;

                if(pn!=null){
                    // 修改x的parent指向n的父节点
                    ln.parent=pn;
                    // 修改p本指向n的子节点指向x
                    if(pn.left==node){
                        pn.left=ln;
                    }else {
                        pn.right=ln;
                    }
                }else{
                    ln.parent=null;
                    this.root=ln;
                }
            }


        }
    }

    public void putVal(K key,V value){
        Node<K,V> node= new Node<K, V>(key, value);
        putVal(node);

    }

    private void putVal(Node<K,V> node){
        Node<K,V> temp=this.root;
        Node<K,V> parent=null;
        //找要插入元素的父节点
        while(temp!=null){
            parent=temp;
            int cmp=temp.key.compareTo(node.key);
            if(cmp>0){
                temp=temp.left;
            }else if(cmp==0){
                temp.value=node.value;
                return;
            }else{
                temp=temp.right;
            }
        }

        //插入元素
        if(parent==null){
            this.root=node;
        }else if(parent.key.compareTo(node.key)>0){
            parent.left=node;
            node.parent=parent;
        }else{
            parent.right=node;
            node.parent=parent;
        }
        // 调用修复红黑树方法。
        fixTree(node);

    }

    /**
     * 1. 根节点为空
     *
     *        直接将node设为根节点，并设置为黑色。
     *
     * 2. 插入节点的key值已存在
     *
     *        直接更新当前节点的值为新节点的值
     *
     * 3. 父节点为黑色
     *
     *        直接插入红色节点，不影响树平衡。
     *
     * 4. 父节点为红色
     *
     *    4.1. 叔叔节点为红色
     *
     *       将父亲节点和叔叔节点染黑。爷爷节点染红。
     *
     *    4.2. 叔叔结点为黑色或为空
     *
     *       4.2.1. 父节点在爷爷节点左侧，子节点在父节点左侧（LL双红）
     *
     *          将父亲节点染黑。爷爷节点染红。对爷爷节点右旋。
     *
     *       4.2.2. 父节点在爷爷节点左侧，子节点在父节点右侧（LR双红）
     *
     *          对父亲节点左旋 然后转-->4.2.1.
     *
     *       4.2.3. 父节点在爷爷节点右侧，子节点在父节点右侧（RR双红）
     *
     *          将父亲节点染黑。爷爷节点染红。对爷爷节点左旋。
     *
     *       4.2.4. 父节点在爷爷节点右侧，子节点在父节点左侧（RL双红）、
     *
     *          对父亲节点右旋 然后转--> 4.2.3.
     * @param node
     */

    public void fixTree(Node<K,V> node){
        // 如果当前节点是黑色，说明这已经是处理过的、合格的红黑树子树了。
        if(!node.isRed()){
            return;
        }
        //1. 如果node是根节点，直接染为黑色
        if(node.parent==null){
            setBlack(node);
            return;
        }
        //父节点
        Node<K,V> parent=node.parent;
        //2. 如果父节点是黑色，就不需要处理，直接插入即可

        /*
          4. 如果父节点是红色，因为插入的节点是红色，红红不能相连，就需要处理
          4.1. 叔叔节点为红色
                将父亲节点和叔叔节点染黑。爷爷节点染红。
          4.2. 叔叔结点为黑色或为空
             4.2.1. 父节点在爷爷节点左侧，子节点在父节点左侧（LL双红）
                    将父亲节点染黑。爷爷节点染红。对爷爷节点右旋。
             4.2.2. 父节点在爷爷节点左侧，子节点在父节点右侧（LR双红）
                    对父亲节点左旋 然后转-->4.2.1.
             4.2.3. 父节点在爷爷节点右侧，子节点在父节点右侧（RR双红）
                    将父亲节点染黑。爷爷节点染红。对爷爷节点左旋。
             4.2.4. 父节点在爷爷节点右侧，子节点在父节点左侧（RL双红）、
                    对父亲节点右旋 然后转-->4.2.3.
         */
        if(isRed(parent)){
            //祖父节点
            Node<K,V> grandParent=parent.parent;
            //叔叔节点
            Node<K,V> uncle=null;
            //寻找叔叔节点
            if(grandParent.left==parent){
                uncle=grandParent.right;
            }else{
                uncle=grandParent.left;
            }

            //4.1 叔叔结点是红色



            if(uncle!=null && isRed(uncle)){
                setBlack(parent);
                setBlack(uncle);
                setRed(grandParent);
                fixTree(grandParent);
                System.out.println("h");
                return;
            }else{
                //4.2 叔叔节点是黑色或为空

                //4.2.1 和 4.2.2 父亲节点是祖父节点的左孩子
                if(parent==grandParent.left){
                    //4.2.2 当前节点是父节点的右孩子
                    if(node==parent.right){
                        // 对当前节点的父亲节点进行左旋操作，此时情况节就转变为4.2.1了。
                        leftSpin(parent);
                        // 更改当前节点。
                        fixTree(node.left);
                        return;
                    }else{//4.2.1 当前节点是父节点的左孩子
                        setBlack(parent);
                        setRed(grandParent);
                        // 对祖父节点右旋
                        rightSpin(grandParent);
                        //更改当前节点
                        //fixTree(parent);
                        return;
                    }


                }else {//父亲节点是祖父节点的右孩子
                    //4.2.4 当前节点是父节点的左孩子
                    if(node==parent.left){
                        // 对当前节点的父亲节点进行右旋操作，此时情况节就转变为4.2.3了。
                        rightSpin(parent);
                        // 更改当前节点。
                        fixTree(node.right);
                        return;
                    }else{//4.2.4 当前节点是父节点的右孩子
                        setBlack(parent);
                        setRed(grandParent);
                        // 对祖父节点左旋
                        leftSpin(grandParent);
                        //更改当前节点
                        fixTree(parent);
                        return;
                    }
                }
            }

        }


    }
    private Node<K,V> getNode(K key){
        Node<K,V> node=this.root;
        int cmp=0;
        while(node!=null){
            cmp=node.key.compareTo(key);
            if(cmp>0){
                node=node.left;
            }else if(cmp<0){
                node=node.right;
            }else {
                return node;
            }

        }
        return null;
    }

    public Node<K,V> deleteNode(K key){
        Node<K,V> node=getNode(key);
        if(node!=null)
            deleteNode(node);

        return node;
    }


    /**
     * 删除指定节点node，
     * 若node是叶子节点，则直接删除即可，
     * 若node不是叶子节点，则需要找到node的前驱或后继节点（这里称为继承者节点），交换继承者节点与被删除节点的键和值（key-value），再去删除继承者节点。
     * 交换继承者节点与被删除节点的键和值后，红黑树仍能保持有序。
     * @param node
     * @return
     */
    public Node<K,V> deleteNode(Node<K,V> node){
        Node<K,V> p=node.parent;
        // 如果是叶子节点，可以直接删除
        if(node.left==null && node.right==null){
            //  若被删除节点是红色，可以直接删除，如果是黑色，直接删除会影响黑高，所以要对红黑树进行修复处理
            if(!node.red)
                fixDelete(node);
            if(p==null) root=null;  //被删除节点是根节点的话，说明root没有子节点，直接将root置空即可
            else{
                //否则就正常地删除，
                node.parent=null;
                if(p.left==node){
                    p.left=null;
                }else {
                    p.right=null;
                }
            }
        }else{  // 如果被删除节点不是叶子节点，就找到node的前驱/后继节点，交换node与前驱/后继节点的值，再删除前驱/后继节点
            Node<K,V> e=getSuccessor(node);
            // 交换被删除节点与继承者节点的键
            K tempKey=e.key;
            e.key=node.key;
            node.key=tempKey;
            // 交换被删除节点与继承者节点的值
            V tempVal=e.value;
            e.value=node.value;
            node.value=tempVal;
            //删除被继承节点
            deleteNode(e);

        }

        return node;

    }


    /**
     * 寻找node的继承者节点。优先返回node的前驱节点，若node没有前驱节点则返回node的后继节点，如果node是叶子节点，则返回null。
     * @param node
     * @return
     */
    Node<K,V> getSuccessor(Node<K,V> node){
        Node<K,V> e;
        //前驱节点： 左子树中，最靠右的叶子节点
        //后继节点： 右子树中，最靠左的叶子节点
        //若左子树不为空，开始寻找node的前驱节点
        if(node.left!=null){
            e=node.left;
            //寻找左子树中最靠右的节点。
            while(e.right!=null){
                e=e.right;
            }
        }else{//若左子树为空，开始寻找node的后继节点节点
            e=node.right;
            //寻找右子树中最靠左的节点
            while(e.left!=null) {
                e = e.left;
            }
        }
        return e;
    }

    /**
     * 在删除操作中，如果被删除节点不是叶子节点，则会删除它的前驱或后继节点，直到被删除节点是叶子节点，所以被删除节点一定是叶子节点。
     * 删除节点后，要修复红黑树的那些性质？
     * 主要修复的是性质4，和性质5 即：
     *      性质4： 每个红色节点的两个自节点一定都是黑色，不能有两个红色节点相连。
     *      性质5： 任意节点到每个叶子节点的路径都包含数量相同的黑节点，称为黑高。
     * 先来考虑，如何保证红黑树的黑高？
     *  红黑树中主要依靠红色节点来平衡黑高，如果以被删除节点的父节点为根节点的子树范围内，有红色节点存在，那么就可以将调整范围控制在此范围内。
     *  如果以被删除节点的父节点为根节点的子树范围内，没有有红色节点存在，就需要扩大调整范围。
     * 对具体情况进行分析（以被删除节点是父节点的右子树为例）
     *  1. 被删除节点是红色
     *      这种情况不影响红黑树的性质，可以直接删除
     *  2. 被删除节点是黑色
     *      2.1. 兄弟节点是黑色，且兄弟节点有红色的子节点
     *          2.1.1. 兄弟节点的左子节点是红色
     *              此时父亲节点的右子树为空，左子树为ll（兄弟节点在父亲节点的左侧，兄弟节点的左子节点在兄弟节点的左侧 left-left），
     *              调整方法：将兄弟节点的颜色染为原来父亲节点的颜色，再将兄弟节点的左子节点和父亲节点染为黑色， 再对父亲节点右旋。
     *              这样此子树的黑高就与删除前的黑高相等，此子树与删除前的子树相比，少了一个红色节点。
     *
     *          2.1.2. 兄弟节点的右子节点是红色
     *              此时父亲节点的右子树为空，左子树为lR（left-right）
     *              对兄弟节点进行左旋，并交换兄弟节点与兄弟节点的右子节点的颜色，就可转换为2.1.1 的情况
     *      2.2.兄弟节点是黑色，兄弟节点的子节点都是黑色； 注：空节点也是黑色
     *          2.2.1. 父节点是红色
     *              将父亲节点染为黑色，兄弟节点染为红色即可
     *          2.2.2. 父节点是黑色
     *              这种情况下，被删除节点、父亲节点、和兄弟节点都是黑色，被删除节点被删除后，不能在以父节点为根节点的范围内，保持黑高不变，
     *              就需要扩大调整的范围。
     *              具体操作为：将兄弟节点染为红色（以父节点为根节点的子树黑高减一），再以父亲节点为删除节点，修复红黑树。
     *      2.3. 兄弟节点是红色（父节点必定为黑色（性质4），且必定有黑色子节点，否则黑高不平衡（性质5））
     *          父亲节点染为红色，兄弟节点染为黑色，再对父亲节点右旋，此时就转换成了2.2.1的情况
     *
     * @param node
     */

    public void fixDelete(Node<K,V> node){
        //记录下父节点
        Node<K,V> parent=node.parent;
        //兄弟节点
        Node<K,V> bro=null;

        if(parent==null){
            node.red=false;
            return;
        }
        // 如果被删除节点是父节点的右子树
        if(node==parent.right){
            // 那么兄弟节点就是父节点的左子节点
            bro=parent.left;

            // 2. 被删除节点是黑色
            if(isBlack(bro)){
                if(isRed(bro.left)){//   2.1.1. 兄弟节点的左子节点是红色
                    bro.red=parent.red; //兄弟节点的颜色设为与父亲节点相同
                    bro.left.red=false; //兄弟节点的左子节点染为黑色。
                    parent.red=false;   //将父亲节点染为黑色。
                    rightSpin(parent);  //对父亲节点右旋，

                }else if(isRed(bro.right)){    //  2.1.2. 兄弟节点的右子节点是红色
                    bro.red=true;  // 将兄弟节点与兄弟节点的右子节点交换颜色。
                    bro.right.red=false;
                    leftSpin(bro);    // 再对兄弟节点左旋,情况就转换成了2.1.1
                    fixDelete(node);  // 再次调用fixDelete（）方法，处理2.1.1的情况
                    return;

                }else {  //  2.2.兄弟节点是黑色，兄弟节点的子节点都是黑色。
                    //2.2.1. 父节点是红色
                    if(parent.red){
                        parent.red=false;   //这种情况下并不影响黑高，这样处理只是模拟2-3树的处理方式，将父亲节点下沉
                        bro.red=true;

                    }else{//    2.2.2. 父节点是黑色
                        bro.red=true;   //将兄弟节点染为红色后，以parent节点为根节点的子树黑高减一，此时需要扩大调整范围，以保证红黑树黑高平衡
                        fixDelete(parent);  //以父节点为被删除节点，调整子树。
                    }
                }


            }else{//    2.3. 兄弟节点是红色
                parent.red=true;    //父亲节点染为红色。
                bro.red=false;      //兄弟节点染为黑色
                rightSpin(parent);  //右旋父亲节点，就转变成了2.2.1的情况
                fixDelete(node);    //再次调用fixDelete()函数，修复2.2.1的情况

            }

        }else{

            bro=parent.right;

            if(isBlack(bro)){

                if(isRed(bro.right)){
                    bro.red=parent.red;
                    bro.right.red=false;
                    parent.red=false;
                    leftSpin(parent);

                }else if(isRed(bro.left)){
                    bro.red=true;
                    bro.left.red=false;
                    rightSpin(bro);
                    fixDelete(node);
                    return;

                }else {


                    if(parent.red){
                        parent.red=false;
                        bro.red=true;

                    }else{
                        bro.red=true;
                        fixDelete(parent);
                    }
                }


            }else{
                parent.red=true;
                bro.red=false;
                leftSpin(parent);
                fixDelete(node);

            }

        }


    }





}

TreeOperation

package src.top.goodbye.test.MapTest;

/**
 * @Auther: csp1999
 * @Date: 2020/11/09/15:10
 * @Description: 打印红黑树的工具类
 */
public class TreeOperation {
    /*
           树的结构示例：
              1
            /   \
          2       3
         / \     / \
        4   5   6   7
    */

    // 用于获得树的层数
    public static int getTreeDepth(RBTree.Node root) {
        return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
    }


    private static void writeArray(RBTree.Node currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
        // 保证输入的树不为空
        if (currNode == null) return;
        // 先将当前节点保存到二维数组中
        res[rowIndex][columnIndex] = String.valueOf(currNode.getKey()+"-"+(currNode.isRed()?"R":"B") /*+ "-" + (currNode.isColor() ? "R" : "B") + ""*/);

        // 计算当前位于树的第几层
        int currLevel = ((rowIndex + 1) / 2);
        // 若到了最后一层，则返回
        if (currLevel == treeDepth) return;
        // 计算当前行到下一行，每个元素之间的间隔（下一行的列索引与当前元素的列索引之间的间隔）
        int gap = treeDepth - currLevel - 1;

        // 对左儿子进行判断，若有左儿子，则记录相应的"/"与左儿子的值
        if (currNode.getLeft() != null) {
            res[rowIndex + 1][columnIndex - gap] = "/";
            writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
        }

        // 对右儿子进行判断，若有右儿子，则记录相应的"\"与右儿子的值
        if (currNode.getRight() != null) {
            res[rowIndex + 1][columnIndex + gap] = "\\";
            writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
        }
    }


    public static void show(RBTree.Node root) {
        if (root == null) System.out.println("EMPTY!");
        // 得到树的深度
        int treeDepth = getTreeDepth(root);

        // 最后一行的宽度为2的（n - 1）次方乘3，再加1
        // 作为整个二维数组的宽度
        int arrayHeight = treeDepth * 2 - 1;
        int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
        // 用一个字符串数组来存储每个位置应显示的元素
        String[][] res = new String[arrayHeight][arrayWidth];
        // 对数组进行初始化，默认为一个空格
        for (int i = 0; i < arrayHeight; i++) {
            for (int j = 0; j < arrayWidth; j++) {
                res[i][j] = " ";
            }
        }

        // 从根节点开始，递归处理整个树
        // res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
        writeArray(root, 0, arrayWidth / 2, res, treeDepth);

        // 此时，已经将所有需要显示的元素储存到了二维数组中，将其拼接并打印即可
        for (String[] line : res) {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < line.length; i++) {
                sb.append(line[i]);
                if (line[i].length() > 1 && i <= line.length - 1) {
                    i += line[i].length() > 4 ? 2 : line[i].length() - 1;
                }
            }
            System.out.println(sb.toString());
        }
    }
}

参考连接

【数据结构】史上最好理解的红黑树讲解，让你彻底搞懂红黑树

小刘讲源码-红黑树原理源码讲解（java）

TreeOperation 打印二叉树源码

最后附上高清修复红黑树的流程图

修复插入操作的流程图

修复删除操作的流程图