状态压缩DP

最新推荐文章于 2024-07-08 22:12:26 发布

吕飞雨的头发不能秃

最新推荐文章于 2024-07-08 22:12:26 发布

阅读量853

点赞数 1

分类专栏：蓝桥杯文章标签：动态规划算法蓝桥杯 python 数据结构

本文链接：https://blog.csdn.net/m0_52711790/article/details/128874372

版权

蓝桥杯专栏收录该内容

46 篇文章 17 订阅

订阅专栏

一、前言

二、状态压缩DP与例题

1、糖果（2019年第十届省赛，lanqiaoOJ题号186）

2、矩阵计数（2019年第十届国赛，lanqiaoOJ题号246）

3、回路计数（2021年第十二届省赛填空题，lanqiaoOJ题号1462）

三、状态压缩DP的原理

1、原理

2、用位运算做集合操作

一、前言

本文讲了状态压缩的例题以及位运算做集合操作的原理。

二、状态压缩DP与例题

1、糖果（2019年第十届省赛，lanqiaoOJ题号186）

【题目描述】

糖果店的老板一共有 M 种口味的糖果出售。为了方便描述，我们将 M 种口味编号 1~M。小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果，而是望 K 颗一包整包出售。幸好糖果包装上注明了其中 K 颗糖果的口味，所以小明可以在买之前就知道每包内的糖果口味。给定 N 包糖果，请你计算小明最少买几包，就可以品尝到所有口味的糖果。

【输入】

第一行包含三个整数 N、M和K。接下来 N 行每行 K 个整数 T1, T2, ..., TK，代表一包糖果的口味 (对于30%的评测用例, 1<=N<=20。对于所有评测样例，1<=N<=100, 1<=M<=20, 1<=K<=20, 1<=Ti<=M。)

【输出】

一个整数表示答案。如果小明无法品尝所有口味，输出-1。

【输入样例】

6 5 3

1 1 2

1 2 3

1 1 3

2 3 5

5 4 2

5 1 2

【输出样例】

2

【暴力法】

对 n 包糖果做任意组合，找到其中一种组合，能覆盖所有口味，并且需要的糖果包数量最少。
n 包糖果的组合共有 2^n 种，暴力法能通过 30% 的测试。n=100 时，严重超时。

【DP】

1）定义状态 dp[i]：表示得到口味组合 i 所需要的最少糖果包数量。

2）状态转移。往口味组合 i 中加入一包糖果，设得到新的口味组合 j，说明从 i 到 j 需要糖果包数量 dp[i]+1。若原来的 dp[j] 大于 dp[i]+1，说明原来得到 j 的方法不如现在的方法，更新dp[j] = dp[i]+1。

【关键问题：如何表示口味组合】

一个方法：为每一包糖果定义一个大小为 m 的数组，记录它的口味。

n 包糖果的口味是一个 n*m 的二维数组，定义为 kw[n][m]。

例：设共有 m=10 种口味， kw[1][] = {0,0,0,0,0,1,0,1,1,0}，表示第一包糖果的口味有三种。

更简单的方法：记录一包糖果的口味，用状态压缩。

【例子说明状态压缩】

例：一包里面有 3 颗糖果，分别是 “2, 3, 5” 三种口味，用一个二进制数 “10110” 表示，这个二进制数的每一位表示一种口味。
使用状态压缩之后，原来需要用二维数组 kw[n][m] 才能表示 n 包糖果的口味，现在只需要一个一维数组 kw[n]。例如 kw[1]=10110，表示第一包的口味是 “2, 3, 5” 三种。
状态压缩 DP 的代码写起来很简洁，因为可以用位运算来简化代码。

1）用状态压缩表示糖果口味

例：输入一包糖果的 “2, 3, 5” 三种口味。

把这 3 个口味压缩成二进制数 10110，做“移位”和“或”操作。

1）定义初始值 tmp = 0。

2）输入口味 “2”。

先移位 1<<(2-1)，得二进制数 10；然后再与 tmp 或，得 tmp = tmp|10 = 10

3）输入口味 “3”。先移位 1<<(3-1)，得二进制数 100；然后再与 tmp 或，得 tmp = tmp|100 = 110

4）输入口味 “5”。先移位 1<<(5-1)，得二进制数 10000；然后再与 tmp 或，得 tmp = tmp|100 = 10110。

代码：tmp = (1<<x-1)

2）dp[]中状态压缩的处理

dp[i]：i表示口味，用状态压缩表示；dp[i] 表示得到口味 i 的最少糖果包数量。
状态转移：同样用到二进制的 “或” 操作。例如 tmp 表示某一包的糖果口味，那么 dp [ i | tmp ] 就表示得到口味 i|tmp 所需要的最少糖果包数量。

n,m,k=map(int,input().split())
tot=(1<<m)-1    #tot：二进制是m个1，表示所有m种口味
dp=[-1 for _ in range(1<<20)]
dp[0]=0
kw=[]
for _ in range(n):
    kw.append([int(i) for i in input().split()])    #kw是二维矩阵
for c in kw:    #用c遍历每个糖果
    tmp=0
    for x in c:
        tmp|=(1<<(x-1))     #用x遍历这包糖果岛口味
    for i in range(tot+1):
        if dp[i]==-1:
            continue        #已存在得到口味i的最少糖果包数量
        newcase=i|tmp
        if dp[newcase]==-1 or dp[newcase]>dp[i]+1:
            dp[newcase]=dp[i]+1
print(dp[tot])              #得到所有口味tot的最少糖果包数量

妙啊，上面这个方法！

2、矩阵计数（2019年第十届国赛，lanqiaoOJ题号246）

【题目描述】

一个 N×M 的方格矩阵，每一个方格中包含一个字符 O 或者字符 X。要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。问这样的矩阵一共有多少种?

【输入描述】

输入一行包含两个整数 N, M (1<=N, M<=5)

【输出描述】

输出一个整数代表答案。

【分析】

很直接的状态压缩 DP。
把方格中的字符 '0'，看成数字 0，字符 'X' 看成数字 1。
把每一行看成一个 m 位的二进制数，例如一行字符 “00X0X” 对应二进制数 “00101”。
一行数字有 2^m 种情况，即范围 [0, 1<<m) 内的数字。这些数字里面只有部分数字符合要求，把这些数存进一个数组 row[]。
要求：这个数字中没有连续的3个1。一个符合要求的数就是这一行的一个合法状态。

定义状态 dp[i][j][k]：第 i 行的合法状态为 j，前一行的合法状态为 k 时，符合条件的矩阵有多少个。

连续 3 行的情况：设第 i 行状态为 j，前一行状态为 k，再前面一行状态为 p，那么 j&k&p 等于0，说明这 3 行没有一列上是3个1。这 3 行是一种合法状态。

状态的递推：

if j&k&p==0:

dp[i][j][k]+=dp[i-1][k][p]

def check(x):       #检查x行中有没有连续3个1
    num=0
    while x:
        if x&1:
            num+=1  #发现一个1
        else:
            num=0
        if num==3:
            return False    #有连续3个1
        x>>=1           #右移一次
    return True

N,M=list(map(int,input().split()))
s=2**M
row=[]                  #合法的行
for i in range(s):      #i的范围：00000~11111
    if check(i):
        row.append(i)

dp=[[[0 for i in range(s)] \
     for j in range(s)] \
    for k in range(N)]      #dp[i][j][k]：第i行的合法状态为j，前一行的合法状态为k时，符合条件的矩阵有多少个

for i in row:
    dp[0][i][0]=1

for i in range(1,N):
    for j in row:       #在所有行都合法的情况下,检查连续3列是否合法
        for k in row:
            for p in row:           #4个for循环，O(N*2^(3m))
                if j&k&p==0:
                    dp[i][j][k]+=dp[i-1][k][p]  

ans=0
for j in row:
    ans+=sum(dp[N-1][j])
print(ans)

3、回路计数（2021年第十二届省赛填空题，lanqiaoOJ题号1462）

【题目描述】

蓝桥学院由 21 栋教学楼组成，教学楼编号 1 到 21。对于两栋教学楼 a 和 b，当 a 和 b 互质时， a 和 b 之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。小蓝现在在第一栋教学楼，他想要访问每栋教学楼正好一次，最终回到第一栋教学楼 (即走一条哈密尔顿回路)，请问他有多少种不同的访问方案？两个访问方案不同是指存在某个 i，小蓝在两个访问方法中访问完教学楼 i 后访问了不同的教学楼。

【Hamilton问题】

Hamilton 问题是 NP 问题，没有多项式复杂度的解法。

暴力解法：枚举 n 个点的全排列。共 n! 个全排列，一个全排列就是一条路径。

本题 n=21，21! = 51,090,942,171,709,440,000

用状态压缩 DP，复杂度下降为 2^n

参考: 《算法竞赛》341页，或者百度搜 “罗勇军博客” 找到 “状态压缩DP”

【状态压缩】

路径起点是1，绕一圈回到 1。

问题转化：1 先到 2~21 中的某个点，然后再绕一圈回到 1。

定义DP。设 S 是图的一个子集，用 dp[S][j] 表示 “集合 S 内的 Hamilton 路径个数”，即从起点 1 出发经过 S 中所有点，到达终点 j 时的路径个数。

最后求所有的访问方案：累加所有的 dp[X][2]~dp[X][21]。

其中 X=1<<22-2，X 是除了点 1 以外的所有其他点。

【哈密尔顿问题与DP】

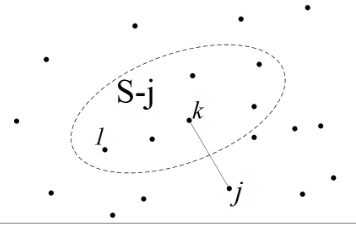
如何求 dp[S][j]？从小问题 S-j 递推到大问题 S。

S-j 表示从集合 S 中去掉 j，即不包含 j 点的集合。

如何从 S-j 递推到 S？设 k 是 S-j 中一个点，把从 1 到 j 的路径分为两部分：(1→...→k)+(k→j)。

以 k 为变量枚举 S-j 中所有的点

状态转移方程：dp[S][j] += dp[S-j][k]

代码：dp[S][j] += dp[S-(1<<j)][k]

from math import gcd
m=1<<22
dp=[[0 for j in range(22)] for i in range(m)]
dist=[[False for j in range(22)] for i in range(22)]
for i in range(1,22):
    for j in range(1,22):
        if gcd(i,j)==1:
            dist[i][j]=True
dp[2][1]=1
for S in range(2,m-1):
    for j in range(1,22):
        if S>>j&i:
            for k in range(1,22):
                if S-(1<<j)>>k & 1 and dist[k][j]:
                    dp[S][j]+=dp[S-(1<<j)][k]
ans=0
for i in range(2,22):
    ans+=dp[m-2][i]
print(ans)

初始化：教学楼编号1到21。教学楼a和b，当a和b互质时，a和b之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。
状态转移：dp[S][j]+=dp[S-(1<<j)][k]
复杂度：3个for循环
m(n^2)=(2^21)(21^2)=924,844,032
运行时间长达10分钟
这题用python很慢，如果用C写，只需运行10秒
如果出题，python组中出状态压缩DP大家很可能都会超时（部分老师会选择不在Python组出状态压缩）

三、状态压缩DP的原理

1、原理

应用背景：以集合为状态，且集合可以用二进制来表示，用二进制的位运算来处理。
集合问题一般是指数复杂度的，例如：1）子集问题，设元素无先后关系，那么共有 2^n 个子集；2）排列问题，对所有元素进行全排列，共有 n! 个全排列。
状态压缩DP：集合的状态 (子集或排列)，如果用二进制表示状态，并用二进制的位运算来遍历和操作，又简单又快。