字符串KMP算法

吕飞雨的头发不能秃

于 2023-03-01 00:41:31 发布

阅读量889

点赞数 4

分类专栏：蓝桥杯文章标签：算法 python 蓝桥杯数据结构

本文链接：https://blog.csdn.net/m0_52711790/article/details/129251466

版权

蓝桥杯专栏收录该内容

46 篇文章 17 订阅

订阅专栏

1、小明的字符串（lanqiaoOJ题号1203）

一、前言

本文主要讲了字符串模式匹配和KMP算法及相关例题。

二、模式匹配

模式匹配 (Pattern Matching) 问题：在一篇长度为 n 的文本 S 中，找某个长度为 m 的关键词 P。称 S 为母串，P 为模式串。
P 可能多次出现，都需要找到。例如在 S="abcxyz123bqrst12dg123gdsa" 中找 P= "123"，P 出现了 2 次。
最优的模式匹配算法复杂度能达到多好？由于至少需要检索文本 S 的 n 个字符和关键词 P 的 m 个字符，所以复杂度至少是 O(m+n) 的。

【朴素方法】

朴素模式匹配算法：一种暴力方法，从S的第一个字符开始，逐个匹配P的每个字符，如果发现不同，就从S的下一个字符重新开始。

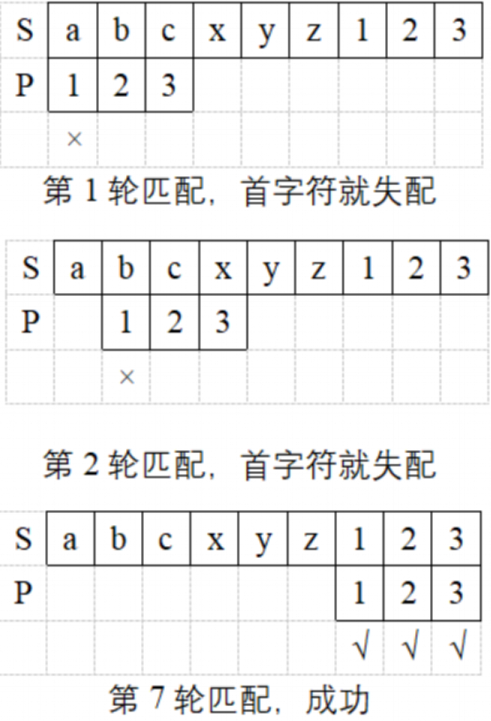
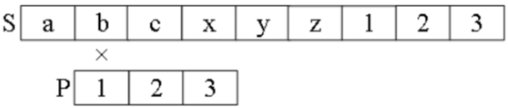
例如 S = “abexyz123”，P= “123”。

第1轮匹配：比较 S[0] ~ S[2] = ”abc” 和 P[0] ~ P[2] = "123"。发现第一个字符就不同，P[0]≠S[0]，称为“失配”，后面的 P[1]、P[2] 不用再比较了。
第2轮匹配…
第7轮匹配…

【暴力法在特殊情况下很好】

特征：P 和 S 的字符基本都不一样。每次匹配时，第 1 个字符就对不上，不用继续匹配 P 后面的字符。复杂度 O(n+m)

【如果情况比较坏】

P 的前 m-1 个都容易找到匹配，

只有最后一个不匹配复杂度退化成 O(nm）。

【朴素法为什么低效】

朴素模式匹配算法：每次失配之后，指向 S 的 i 指针都要回溯，而 P 的 j 指针都要回到 0，重新开始下一轮的匹配。这是朴素算法低效的原因。
每次新的匹配都需要重新对比 S 和 P 的全部 m 个字符，这做了重复操作。
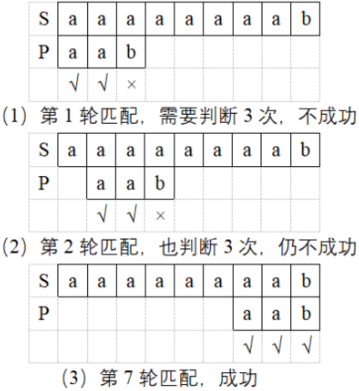
例如第一轮匹配 S 的前 3 个字符 "aaa" 和 P 的 "aab"，第二轮从 S 的第 2 个字符 ‘a' 开始，与和 P 的第一个字符 ‘a’ 比较，这其实不必要，因为在第一轮比较时已经检查过这两个字符，知道它们相同。
如果记住每次的比较，用于指导下一次比较，使得 S 的 i 指针不用回溯，就能提高效率。

三、KMP算法

KMP算法：在任何情况下都能达到 O(n+m) 复杂度。
朴素模式匹配算法的缺点：每次失配之后，指向 S 的 i 指针都要回溯，而 P 的 j 指针都要回到 0，重新开始下一轮的匹配。
KMP算法：S 的 i 指针不用回溯，极大优化了匹配计算。

这时候我们就得思考了，如何让 S 的指针 i 不回溯，P 的指针 j 不回到 0?

1）P在失配点之前的每个字符都不同

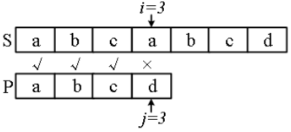
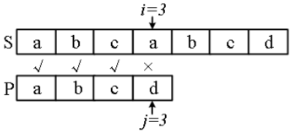
S=“abcabcd”，P=“abcd”，第一次失配点：i=3，j=3。

失配点之前的 P 的每个字符都不同：P[0]≠P[1]≠P[2]；

失配点之前的 S 与 P 相同：P[0]=S[0]、P[1]=S[1]、P[2]= S[2]。

下一步如果按朴素方法，j 要回到位置 0，i 要回溯到1，去比较 P[0] 和 S[1]。

KMP 的优化：不用 i 回溯。
从 P[0]≠P[1]、 P[1]=S[1] 推出 P[0]≠S[1]，所以 i 不用回溯到位置 1。
同理，P[0]≠S[2]，i 也不用回溯到位置 2。
所以完全不用回溯，继续从 i=3、j=0 开始下一轮的匹配。

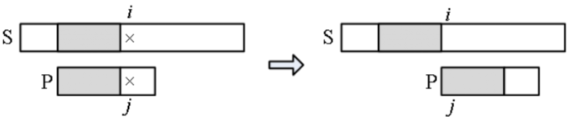
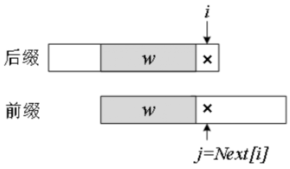
当 P 滑动到左图位置时，i 和 j 所处的位置是失配点，S 与 P 的阴影部分相同，且阴影内部的字符都不同。下一步直接把 P 滑到 S 的 i 位置，此时 i 不变、j 回到0，然后开始下一轮的匹配。

2）P在失配点之前的字符有部分相同

再细分两种情况：

①相同的部分是前缀（位于 P 的最前面）和后缀（在 P 中位于 j 前面的部分字符）。

②相同部分不是前缀或后缀。

【相同的部分是前缀和后缀】

前缀和后缀的定义：

字符串 A 和 B，若存在 A = BC，其中 C 是任意的非空字符串，称 B 为 A 的前缀；

同理可定义后缀，若存在 A = CB，C 是任意非空字符串，称 B 为 A 的后缀。

例：A="abcxyabc"，它有 7 个前缀 { a, ab, abc, abcx, abcxy, abcxya, abcxyab}，也有 7 个后缀 {bcxyabc, cxyabc, xyabc, yabc, abc, bc,c}，前缀和后缀中相同的是 "abc"。

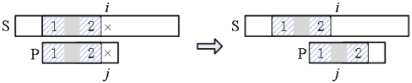
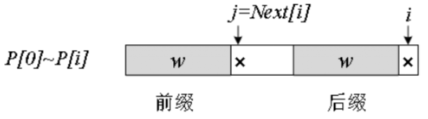
当 P 滑动到左图位置时，i 和 j 所处的位置是失配点，j 之前的部分与 S 匹配，且子串 1（前缀）和子串 2（后缀）相同，设子串长度为 L。下一步把 P 滑到右图位置，让 P 的子串 1 和 S 的子串 2 对齐，此时 i 不变、j=L，然后开始下一轮的匹配。

S 的 i 指针不用回溯，P 的 j 指针也不用回到 0，而是直接跳回到 L 位置，大大减少了计算量。把 P 的相同的前缀和后缀定义为 “公共前后缀”，L 等于 “最长公共前后缀”。

【相同的部分不是前缀和后缀】

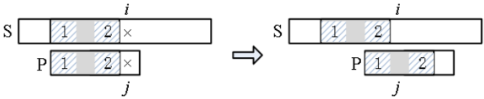
左图，P 滑动到失配点 i 和 j，前面的阴影部分是匹配的，且子串 1 和 2 相同，但是 1 不是前缀（或者 2 不是后缀），这种情况与 “1）P 在失配点之前的每个字符都不同” 类似，下一步滑动到右图位置，即 i 不变，j 回溯到 0。

【最长公共前后缀和 Next[ ] 数组】

不回溯 i 完全可行。
关键在于 P 的前缀和后缀。
计算每个 P[] 的前缀、后缀，记录在 Next[] 数组中，Next[j] 的值等于 P[0]~P[j-1] 这部分子串的前缀集合和后缀集合的最长交集的长度，把这个最长交集称为 “最长公共前后缀”。

【next数组的计算】

例：P=“abcaab”，计算过程如下表，每一行的红色子串是最长公共前后缀。

计算 Next[]：复杂度 O(m) 的方法，利用前缀和后缀的关系，从 Next[i] 递推到 Next[i+1]。

假设已经算出 Next[i]，它对应 P[0]~P[i-1] 这部分子串的后缀和前缀。

阴影部分 w 是最长交集，交集 w 的长度等于 Next[i]。

上半部分的阴影所示的后缀的最后一个字符是 P[i-1]；

下半部分阴影所示前缀的第一个字符是 P[0]，最后一个字符是 P[j]，j = Next[i]-1。

推广到 Next[i+1]，它对应 P[0]~P[i] 的后缀和前缀。此时后缀的最后一个字符是 P[i]，与这个字符相对应，把前缀的 j 也往后移一个字符，j=Next[i]。

判断两种情况：

1) 若 P[i]=P[j]，则新的交集等于 “阴影 w+P[i]”，交集的长度 Next[i+1]=Next[i]+1。

2) 若 P[i]≠P[i]，说明后缀的 “阴影w+P[i]” 与前缀的 “阴影w+P[j]” 不匹配，只能缩小范围找新的交集。

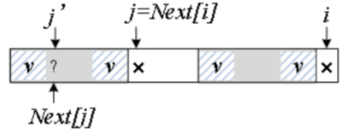
下图合并了前缀和后缀，画出完整的子串 P[0]~P[i]，最后的字符 P[i] 和 P[j] 不等。

把前缀往后滑动，也就是通过减小 j 来缩小前缀的范围，直到找到一个匹配的 P[i]=P[j] 为止。如何减小 j ? 只能在 w 上继续找最大交集，这个新的最大交集是 Next[i]，所以更新j'=Next[j]。

下图斜线阴影 v 是 w 上的最大交集，下一步判断：

若 P[i] = P[j']，则 Next[i+1] 等于 v 的长度加 1，即 Next[j']+1；

若 P[i] ≠ P[j']，继续更新 j'。

四、例题

1、小明的字符串（lanqiaoOJ题号1203）

【题目描述】

小明有两个字符串，分别为 S,T。请你求出 T 串的前缀在 S 串中出现的最长长度为多少。

【输入描述】

输入包含两行，每行包含一个字符串，分别表示 S，T。1≤|S|, |T|≤10^6，保证 S, T 只包含小写字母。

【输出描述】

输出共1行，包含一个整数，表示答案。

【思路】

本题求 T 的前缀在 S 中出现的最长长度。简单的思路是：枚举 T 的每个前缀，对每个前缀，用 KMP 到 S 中找这个前缀，在所有匹配到的前缀中找最长的，就是答案。
不过，其实并不需要做多次 KMP，只做一次 KMP 即可。
回顾 KMP 算法，是用 P 匹配 S，逐个移动 P 的指针 j，直到失配为止，失配之前的 P 的前缀在 S 中匹配到了。那么只要记录匹配到的最长前缀，就是题目要求的答案。这是 KMP 算法的裸题。

N=1000005
Next=[0]*N
def getNext(p):         #计算Next[1]~Next[plen]
    for i in range(1,len(p)):   
        j=Next[i]           #j的后移:j指向前缀阴影w的后一个字符
        while j>0 and p[i]!=p[j]:   #阴影的后一个字符不相同
            j=Next[j]               #更新j
        if p[i]==p[j]:
            Next[i+1]=j+1
        else:
            Next[i+1]=0
def kmp(s,p):
    ans=0
    j=0
    for i in range(0,len(s)):   #匹配S和P的每个字符,S的i指针，它不回溯，用for循环一直往前走。
        while j>0 and s[i]!=p[j]:   #失配了
            j=Next[j]           #j滑动到Next[j]位置
        if s[i]==p[j]:      #当前位置的字符匹配，继续
            j+=1
            ans=max(ans,j)
        if j==len(p):
            return ans      #最长前缀就是p的长度，直接返回
    return ans              #返回p在s中出现的最长前缀
s=input()
t=input()
getNext(t)
print(kmp(s,t))