【科普】快速读懂复杂网络

引言

随着近几年关于复杂网络（Complex network）理论及其应用研究的不断深入，已有大量关于复杂网络的文章发表在Science，ature，RL，NAS等国际一流的刊物上，侧面反映了复杂网络已经成为物理界的一个新兴的研究热点。人们开始尝试应用这种新的理论工具来研究现实世界中的各种大型复杂系统，其中复杂系统的结构以及系统结构与系统功能之间的关系是人们关注的热点问题。
在自然界中存在的大量复杂系统都可以通过形形色色的网络加以描述。一个典型的网络是由许多节点与节点之间的连边组成，其中节点用来代表真实系统中不同的个体，而边则用来表示个体间的关系，往往是两个节点之间具有某种特定的关系则连一条边，反之则不连边，有边相连的两个节点在网络中被看作是相邻的。例如，神经系统可以看作大量神经细胞通过神经纤维相互连接形成的网络[2]；计算机网络可以看作是自主工作的计算机通过通信介质如光缆、双绞线、同轴电缆等相互连接形成的网络[2]。类似的还有电力网络[3]、社会关系网络[2,4-5]、交通网络[6]、调度网络[7]等等。
复杂网络的研究由于其学科交叉性和复杂性的特点，涉及了众多学科的知识和理论基础，尤其是系统科学、统计物理、数学、计算机与信息科学等，常用的分析方法和工具包括图论、组合数学、矩阵理论、概率论、随机过程、优化理论和遗传算法等。复杂网络的主要研究方法都是基于图论的理论和方法开展的，并已经取得了可喜的成果。但近几年，统计物理的许多概念和方法也已成功地用于复杂网络的建模和计算，如统计力学、自组织理论、临界和相变理论、渗流理论等[8]，如网络结构熵的概念，并用它来定量地度量复杂网络的“序”。复杂网络模型在很多科学领域都得到广泛的应用。

参考文献：

[1] 孙玺菁, 司守奎. 复杂网络算法与应用[M]. 国防工业出版社, 2015.

[2] Watts D J, Strogatz S H. Collective dynamics of 'small-world' networks.[J]. Nature, 1998, 393(6684):440.

[3] Faloutsos M, Faloutsos P, Faloutsos C. On power-law relationships of the Internet topology[J]. Acm Sigcomm Computer Communication Review, 1997, 29(4):251-262.

[4] Hofman J M, Sharma A, Watts D J. Prediction and explanation in social systems.[J]. Science, 2017, 355.

[5] Ebel H, Mielsch L I, Bornholdt S. Scale-free topology of e-mail networks[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2002, 66(3 Pt 2A):035103.

[6] 吴文祥, 黄海军. 固定需求交通网络的一般系统最优模型与性质[J]. 管理科学学报, 2015, 18(12):58-67.

[7] 宣琦,吴铁军. 复杂open shop问题的网络模型及调度规则设计[J]. 浙江大学学报(工学版),2011,(06):961-968.

[8] Albert R, Barabási A. Statistical mechanics of complex networks[J]. Review of Modern Physics, 2002, 74(1):47-97.

1. 复杂网络的研究历史

1736，欧拉：哥尼斯堡七桥问题；1950，Erdos, Renyi: 随机图论；1998，Strogatz, Barabasi:小世界和无标度网络。
参考：https://zhuanlan.zhihu.com/p/35705787

从这十几年的研究来看，之所以称其为复杂网络，致少包含以下几层意思：首先，它是大量真实复杂系统的拓扑抽象；其次，它至少在感觉上比规则网络和随机网络复杂，因为我们可以很容易地生成规则和随机网络，但就目前而言，还没有一种简单方法能够生成完全符合真实统计特征的网络；最后，由于复杂网络是大量复杂系统得以存在的拓扑基础，此对它的研究被认为有助于理解“复杂系统之所以复杂”这一至关重要的问题。

2. 复杂网络的统计特征

2.1平均路径长度L

在网络中，两点之间的距离为连接两点的最短路径上所包含的边的数目。网络的平均路径长度指网络中所有节点对的平均距离，它表明网络中节点间的分离程度，反映了网络的全局特性。不同的网络结构可赋予L不同的含义。如在疾病传播模型中L可定义为疾病传播时间，通网络模型中L可定义为站点之间的距离等。

2.1度相关性

对于某一个网络而言，令D={d1,d2,…,dn} ，其中di 代表的是节点i=1,2,3…,n 的度值。N为网络的节点总数。用(i,j)∈E 来表示节点i 和节点j 之间的连边

2.1最大连通集团

网络一般由多个分支组成，一个分支指的是一个连通的子网络，“最大”代表着原网络中任何其它节点或边遭受到攻击时，形成大小不一的连通子图。把连通子图中阶数最大的一个称为最大连通分支，即最大连通子图，当网络演化成无限网络时，最大连通分支的阶数与整个网络的阶数之比对不同的网络会呈现出不一样的结果，这一比值是衡量网络稳定性的一个重要参数，同时也是网络渗流相变理论中的一个重要参考量。同时，也能从某些方面说明网络的鲁棒性好坏。

2.1度及度分布

在网络中，点的度是指与该节点相邻的节点的数目，即连接该节点的边的数目。而网络的度指网络中所有节点度的平均值。度分布P(k)指网络中一个任意选择的节点，它的度恰好为k的概率。

2.3聚集系数C

在网络中，节点的聚集系数是指与该节点相邻的所有节点之间连边的数目占这些相邻节点之间最大可能连边数目的比例。而网络的聚集系数则是指网络中所有节点聚集系数的平均值，它表明网络中节点的聚集情况即网络的聚集性，也就是说同一个节点的两个相邻节点仍然是相邻节点的概率有多大，它反映了网络的局部特性。

2.4介数

包括节点介数和边介数。节点介数指网络中所有最短路径中经过该节点的数量比例，边介数则指网络中所有最短路径中经过该边的数量比例。介数反映了相应的节点或边在整个网络中的作用和影响力。

2.5小世界效应

复杂网络的小世界效应是指尽管网络的规模很大(网络节点数目N很大)，但是两个节点之间的距离比我们想象的要小得多。也就是网络的平均路径长度L随网络的规模呈对数增长，即L～In N。大量的实证研究表明，真实网络几乎都具有小世界效应。

2.6无标度特性

对于随机网络和规则网络，度分布区间非常狭窄，大多数节点都集中在节点度均值的附近，说明节点具有同质性，因此可以被看作是节点度的一个特征标度。而在节点度服从幂律分布的网络中，大多数节点的度都很小，而少数节点的度很大，说明节点具有异质性，这时特征标度消失。这种节点度的幂律分布为网络的无标度特性。

3. 各种网络模型

3.1 规则网络

最简单的网络模型为规则网络，它是指系统中各元素之间的关系可以用一些规则的结构表示，也就是说网络中任意两个节点之间的联系遵循既定的规则，通常每个节点的近邻数目都相同。常见的具有规则拓扑结构的网络包括全局耦合网络（也称为完全图）、最近邻耦合网络和星型耦合网络。

3.2 随机网络

从某种意义上讲，规则网络和随机网络是两个极端，而复杂网络处于两者之间。节点不是按照确定的规则连线，如按纯粹的随机方式连线，所得的网络称为随机网络。如果节点按照某种自组织原则方式连线，将演化成各种不同网络。

3.3 小世界网络

规则的最近邻耦合网络具有高聚类特性，但并不是小世界网络。另一方面，ER随机网络虽然具有小的平均路径长度但却没有高聚类特性。因此，这两类网络模型都不能再现真实网络的一些重要特征，毕竟大部分实际网络既不是完全规则的，也不是完全随机的。作为从完全规则网络向完全随机网络的过渡，Watts和Strogtz于1998年引入了一个小世界网络模型，称为WS小世界模型。

3.4 无标度网络

很多网络（包括Internet和新陈代谢网络等）都不同程度拥有如下共同特性：大部分节点只有少数几个链接，而某些节点却拥有与其他节点的大量链接，表现在度分布上就是具有幂律形式，即P(k)~k—γ。这些具有大量链接的节点称为“集散节点”，所拥有的链接数可能高达几百、几千甚至几百万。包含这种集散节点的网络，由于网络节点的度没有明显的特征长度，故称为无标度网络。

3.5 自相似网络

自相似是相似中的一种特殊情况，它是指系统的部分和整体之间具有某种相似性，这种相似性不是两个无关事物间的偶然近似，而是在系统中必然出现并始终保持的。这种自相似是层次复杂网络共有的拓扑性质，而自相似又是分型的一个基本特征，所以复杂系统与各层次子系统之间的自相似性，可以利用分形加以描述。

4. 复杂网络主要研究内容及应用

4.1 主要研究内容

复杂网络模型：
典型的复杂网络：

• 随机网、小世界网、无标度网等；
• 实际网络及其分类。

网络的统计量及与网络结构的相关性：

• 度分布的定义和意义，聚集性、连通性的统计量及其实际意义等。

复杂网络性质与结构的关系：

• 同步性、鲁棒性和稳定性与网络结构的关系。

复杂网络的动力学：

• 信息传播动力学、网络演化动力学、网络混沌动力学。

复杂网络的复杂结构：

• 社团结构、层次结构、节点分类结构等。

网络控制：

• 关键节点控制、主参数控制和控制的稳定性和有效性。

4.2 复杂网络的应用

复杂网络与生物体的新陈代谢系统、大脑神经网络相结合；
复杂网络与生物传染病相结合、在流行病传播与免疫控制方面的研究；
复杂网络上的博弈；
复杂网络在交通网络与社会经济中的应用；
复杂网络在通信网络中的应用；
复杂网络在计算机网络与互联网中的应用；
复杂网络在传感器网络中的应用；
复杂网络在语言词汇网络和社会意见传播等方面的应用等。

• 技术网络：
  计算机互联网络已经发展成为一个巨大的复杂系统，网络的数以千万计的终端用户通过网关和路由器（网络节点）相连，形成一个非常复杂的不规则的拓扑结构而且，越来越多的信息按照协议通过互联网络由各种信息资源传给不同的终端用户(随着用户数量和网络连接的迅猛增加，网络拓扑结构更为复杂，导致网络传输速率下降和等待时间加长，从而使得网络拥塞网络的拥塞又使得人们不停的改进网络协议和操作系统、增加网络带宽、增加和优化网络资源，以利于网络更为有效合理的使用。
  
  现实世界中的许多系统都可以用复杂网络来描述，力系统是人类创造的最为复杂的网络系统之一。当前经典的网络模型与实际电力网络存在较大差异。从电力网络本身的演化机理入手，提出并研究了一种可以模拟电力网络演化规律的新型局域世界网络演化模型。
  

• 社会网络：
  朋友关系网作为一种典型的社会网络，受到了复杂网络领域诸多学者的关注。顾名思义，朋友关系网是根据人们之间的朋友关系所建立的网络，以人为节点，两人之间若有朋友关系则连接一条边。一些学者之前对朋友关系网的研究也获得了许多成果。
  
  引文网络是体现知识生产、传播过程的一个重要方面。随着知识量的迅速增长，引文网络已经形成了一个超大规模的网络系统。然而，科学计量学领域中关于大型引文网络的研究还非常少，关于引文网络中知识生产和传播过程的研究更是少有涉及。
  本文立足于科学学引文网络，整合复杂网络理论和社会网络分析方法，从宏观、微观和中观三个层面对科学学的引文网络进行研究，探讨网络的结构及其对知识的流动传播产生的影响。 对从SCI中下载的数据进行了权威控制并对其进行纠错，力图使研究最接近于真实情况。在此基础上对科学学引文网络的整体结构进行了研究，发现科学学引文网络同时具有复杂网络的“无标度”、“小世界”和“高集聚”的特性。科学学引文网络的整体结构适宜于知识快速流动，但是知识传播的路径还有待于进一步的优化。
  

• 交通运输网络：
  -在城市道路交通网络中，于恶劣天气、交通事件等可能造成一个或少数关键路段或路口失效(如堵塞)，些失效路段或路口会通过路段、路口间的相互关联引起其它路段或路口失效，成连锁效应，终导致整个网络或局部崩溃，就是级联失效。
  
  基于整个航空运输网络研究航班延误及其产生的次生衍生突发事件链式效应。以航班延误为中心，讨航班延误及其波及的发生发展过程，立基于阶段细分的航班延误波及模型；

根据导致航班延误的原因以及次生衍生事件链式效应规律，航班延误的理由及其波及导致的下游航班或下游机场航班延误等一系列次生衍生事件链，建航班延误次生衍生事件链式网络；

通过建立航空运输网络结构，拟航班延误及其次生衍生事件链式效应的传播扩散过程，精确预测航班延误引发的次生衍生事件，量分析航班延误波及效应的影响程度。有助于民航应急管理部门有针对性地预防和管控航班延误可能发生的次生衍生事件，而有效地缓解由航班延误波及引发的次生衍生事件的后果与影响，低航班延误的损失。

随着城市化进程的加速，人们出行日益增加，城市的交通拥堵问题越来越严重。公共交通是解决城市拥堵问题最为有效的途径，而城市公共交通网络容量是城市公共交通的一项重要研究。大量的研究如，如何定义城市公共交通网络容量；如何确定影响因素以及计算容量的大小。

• 生物网络：
  生态网络是对生态系统中物质、能量流动进行模拟的结构模型。生态网络分析是指对生态网络进行分析的方法和理论。它在年代后期开始引起人们的注意。其领域涉及生态网络流动分析、信息分析、随机分析、结构分析以及灵敏度分析等。它是系统生态学的重要分支。
  
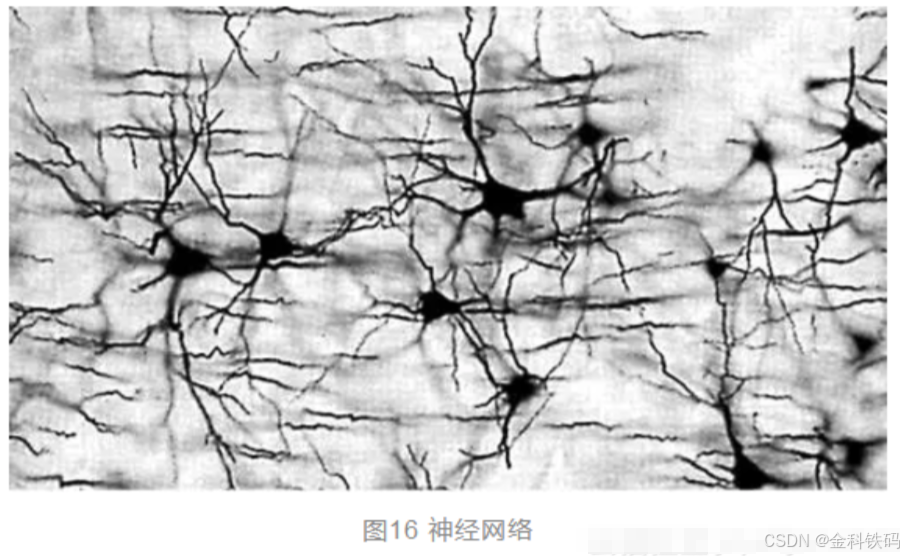
  人脑是由大量的神经元细胞组成的，神经元的工作产生了人脑的智能，人脑的研究导致了神经网络这一门学科的诞生，以说脑科学和神经科学的发展对神经网络研究的进展起到了很大的帮助和引领作用。模拟人类或者其他高级灵长类动物、哺乳动物、鸟类等的视觉、听觉、语言理解等功能的原理，是神经网络研究的初衷，这也是为什么神经网络领域的研究常常和脑科学以及神经学、认知学等领域存在交叉。

由此而发展起来的机器学习可以分为两大类：有监督学习和无监督学习。有教师监督的学习指的是所学习的数据样本是标注好的，学习模型在学习的时候知道要学习的结果是什么样，然后根据已知的结果去调节学习的过程和模型本身的参数，监督学习指的是数据样本没有标注，学习模型无法得知学习的最终结果，能按照一定的规则去学习未知的结果。