数据挖掘3-4-5规则详解

最近在准备数据挖掘的期末考试，在第三章数据预处理中的数据变换与离散化问题中，利用3-4-5规则进行概念分层，没看懂老师ppt，所以写下此篇博客，用以记录利用3-4-5规则进行概念分层的问题求解。

首先先明确3-4-5规则：

如果一个区间最高有效位上跨越3，6，7或9个不同的值，就将该区间划分为3个等宽子区间；

如果一个区间最高有效位上跨越2，4，或8个不同的值，就将该区间划分为4个等宽子区间；

如果一个区间最高有效位上跨越1，5，或10个不同的值，就将该区间划分为5个等宽子区间；

将该规则递归的应用于每个子区间，产生给定数值属性的概念分层；

 

问题：

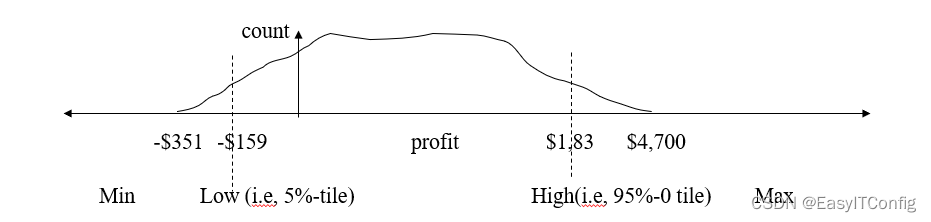
对该数据进行离散化（利用3-4-5规则构造概念层次数）

---

对该问题的求解主要掌握最高有效位的概念即可，下面以一个具体的例子来理解：

而对于本题来讲，共划分为2个问题：

• 对5%~95%的区间进行3-4-5规则
• 对0~5%、95%~1的区间进行3-4-5规则

由图中可以看出对于5%~95%的区间:

其low=-159，high=1838，故按照规则，其跨越-1、0、1三个数（(-159)/10^3 =-0.159=-1， 1838/10^3 =2），划分3个等宽区间，故可划分为(-1000,0)、(0,1000)、(1000,2000) 

对0~5%、95%~1的区间进行调整:

min=-351，max=4700，其中min向下取整-400属于（-1000，0）区间，故将左区间改为（-400，0），4700向上取整得5000，并没有该区间，故新增(2000,5000)区间，故最终区间为(-400,0)、(0,1000)、(1000,2000)、(2000,5000)
对上述区间再次进行划分形成较低层:

• (-400,0)中，跨-4，-3，-2，-1，划分4个等区间：(-400,-300),(-300,-200),(-200,-100),(-100,0)
• (0,1000)中，跨0，划分5个等区间：(0,200),(200,400),(400,600),(600,800),(800,1000)
• (1000,2000)中，跨1，划分5个等区间：(1000,1200),(1200,1400),(1400,1600),(1600,1800),(1800,2000)
• (2000,5000)中，跨越2，3，4，划分为3区间：(2000,3000),(3000,4000),(4000,5000)