傅里叶变换的简单介绍（Fourier Transform, FT）

定理1 组成三角级数的函数系

        1, cos x, sin x, cos 2x, sin 2x, ..., cos nx, sin nx, ...在[-Π，Π]上正交，即其中任意两个不同的函数之积在[-Π，Π]上的积分为0。

定理2 设f(x)是周期为2Π的周期函数，且

右端级数可逐项积分，则

定理3 （收敛定理，展开定理）设f(x)是周期为2Π的周期函数，并满足狄利克雷( Dirichlet )条件：

        （1）在一个周期内连续或只有有限个第一类间断点；

        （2）在一个周期内只有有限个极值点

则f(x)的傅里叶级数收敛，且有

其中,为f(x)的傅里叶系数 

一、傅里叶级数（Fourier Series）

1.1 三角函数形式的傅里叶级数

1.1.1 三角函数集

        三角函数集 {1, 𝑐𝑜𝑠𝑥, 𝑠𝑖𝑛𝑥, 𝑐𝑜𝑠2𝑥, 𝑠𝑖𝑛2𝑥, … … , 𝑐𝑜𝑠𝑛𝑥, 𝑠𝑖𝑛𝑛𝑥 }, (𝑛 = 1,2,3 … … , ∞), 内的函数在区间[−𝜋, 𝜋] 上彼此正交。

1.1.2 级数形式

周期信号 f (t),周期为T，基波角频率为ω = 2Π / T

在满足狄利克雷条件时，可展成

称为三角形式的傅里叶级数，其系数

1.2 指数函数形式的傅里叶级数

1.2.1 复指数正交函数集

 1.2.2 级数形式

1.2.3 系数 利用复变函数的正交特性

 周期信号f(t)的傅里叶级数有两种形式

① 三角形式

② 指数形式

 二、傅里叶变换

 2.1 直角坐标系内的二维傅里叶变换

        二元函数f(x,y)的傅里叶变换(即傅里叶谱或频谱)定义为

        其傅里叶逆变换定义为

 

         非周期函数可分解为连续频率的余弦分量的积分，F()是各频率成分的权重因子（weighting factor）。

 2.2 极坐标系内的二维傅里叶变换

2.2.1 定义式

2.2.2  傅里叶－贝塞尔变换

        式中是第一类零阶贝塞尔函数(is a Bessel function of first kind, zero order)，与无关，表明圆对称函数的傅里叶变换和逆变换仍为圆对称。

三、广义傅里叶变换

 3.1 极限意义下的傅里叶变换

如果f(x)和一个函数序列(x)具有以下关系

而且函数序列中的每一个函数(x)，其狭义傅里叶变换

存在，且在n趋于无穷时，函数序列（）也有确定的极限，则定义

3.2 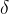函数的傅里叶变换 

 即(x)的傅里叶变换是常数1

且常数1的傅里叶逆变换等于(x)，因此存在

类似的还有

四、常用的傅里叶变换对