菲涅耳衍射和夫琅禾费衍射

一、菲涅耳衍射（傍轴近似）

1.1 空域表示

观察平面上复振幅分布：

采用傍轴近似：

　假定观察平面和孔径平面之间的距离 z 远远大于孔径 Σ 以及观察区域的最大线度。

菲涅耳近似的物理实质是用二次曲面来代替球面波的惠更斯子波。

菲涅耳衍射公式：

        尽管孔径有一定大小，而对观察点有真正贡献的只是孔径上 x=x0 , y=y0点附近的小区域。因此菲涅尔衍射是很容易实现的。

菲涅耳衍射的脉冲响应：

菲涅耳衍射的傅里叶变换表示：

1.2 空间频谱或角谱表示

菲涅耳衍射的传递函数：

二、夫琅禾费衍射（远场近似）

2.1 空域表示

脉冲响应为：

不再具有平移不变性.

 衍射光场分布为：

空域中，不再具有卷积形式.

夫琅禾费衍射仍是线性系统，但不是平移不变系统， 不再具有平移不变性.

2.2 频域表示

对此式左右两端作傅里叶变换，得

在频域中可表示成卷积形式。

三、夫琅禾费衍射与菲涅耳衍射的比较

3.1 衍射图样

（1）二者的积分号前面都有

该项对衍射光强的相位分布有影响，但对强度分布形式无影响。

（2）菲涅耳衍射的光场分布正比于

的傅里叶变换，因此，随着 z 的增加，观察平面上光场分布(及强度)发生变化，仅就z轴上的点而言，随 z的增加其亮暗是交替变化的.

        夫琅禾费衍射的光场分布正比于衍射屏出射光场U0(x0 , y0)的傅里叶变换，当 z 变化时，衍射图样只是按比例放大或缩小；图样形状不会发生变化，中心点不会出现亮暗交替变化.

3.2 关于近似条件

菲涅耳近似:

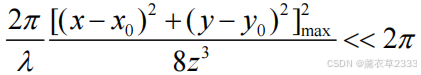
夫琅禾费近似：

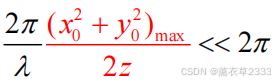
夫琅禾费近似是比菲涅耳近似更强的近似。

要在近距离上观察到夫琅禾费衍射，关键是要消除菲涅耳衍射积分公式中的

可有两种方法：

(1) 用会聚球面波照射，在其会聚点上放置观察屏；

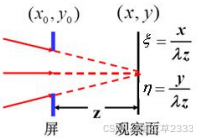
(2) 在衍射屏和观察平面之间放置一个会聚透镜，用平面波入射.

3.3 两者之间的关系

        在夫琅禾费衍射近似条件满足的范围内，菲涅耳衍射近似条件肯定满足，菲涅耳衍射的范围包含了夫琅禾费衍射范围. 可以利用菲涅耳衍射积分公式计算夫琅禾费衍射，反之则不行.

通常将光的衍射分为三种类型：瑞利-索末菲衍射、 菲涅耳衍射(近场衍射)和夫琅禾费衍射(远场衍射)。

四、关于脉冲响应及传递函数

4.1 菲涅耳衍射

具有线性平移不变性，有传递函数，空域中可以写成卷积形式，频域中可写成乘积形式。

4.2 夫琅禾费衍射

        夫琅禾费近似破坏了积分公式的平移不变性. 具有线性, 但不具有平移不变性. 不存在专门与夫琅禾费衍射对应的传递函数. 不能写成卷积形式, 也不能写成频谱乘积的形式.

        夫琅禾费衍射只不过是菲涅耳衍射的极限情况(即菲涅耳衍射区包含了夫琅禾费衍射区), 菲涅耳衍射的传递函数对夫琅禾费衍射仍然保持有效, 只是 z 值要足够大而已.

        由角谱理论得出的传递函数, 对菲涅耳衍射和夫琅禾费衍射都适用.