一阶问题举例:
高阶问题举例 :

常微分方程数值解:向前欧拉方法之一阶问题
clc,clear,close all;
a=0;%初始时刻
b=2*pi;%结束时刻
n=100;%离散点数量
x0=0;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
fun=inline('sin(x)+y','x','y');
y0=1;%计算
y(1)=y0;
for i=1:n %迭代
f=feval(fun,x(i),y(i));
y(i+1)=y(i)+h*f;
end
plot(x,y,'o');hold on
n=1000;
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
for i=1:n
f=feval(fun,x(i),y(i));
y(i+1)=y(i)+h*f;
end
plot(x,y,'-');
常微分方程数值解:向前欧拉方法之高阶问题
clc,clear,close all;
a=1;%初始时刻
b=10;%结束时刻
n=100;%离散点数量
x0=1;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
y0=[1,10,30];%计算
y(1,:)=y0';
for i=1:n %迭代
f=feval('fun_3rd',x(i),y(i,:));%x是标量,y是向量
%feval()函数执行指定的函数。
%将想要执行的函数以及相应的参数一起作为feval()的参数,
%feval()的输出等于想要执行的函数的输出。
f=f';
y(i+1,:)=y(i,:)+h*f;
end
plot(x,y(:,1),'o');%所有的行的第一列
龙格库塔方法(精确度高):一阶问题
clc,clear,close all;
a=0;%初始时刻
b=2*pi;%结束时刻
n=1000;%离散点数量
x0=0;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
fun=inline('sin(x)+y','x','y');
y0=1;
%计算
y(1)=y0;
for i=1:n %迭代
k1=feval(fun,x(i),y(i));
k2=feval(fun,x(i)+h/2,y(i)+h*k1/2);
k3=feval(fun,x(i)+h/2,y(i)+h*k2/2);
k4=feval(fun,x(i)+h,y(i)+h*k3);
y(i+1)=y(i)+h*(k1+2*k2+2*k3+k4)/6;
end
plot(x,y,'o');龙格库塔方法(精确度高):高阶问题
%龙格库塔方法
%高阶问题,内置函数
%[a,b]=ode45('fun_3rd',[1,10],[1 10 30])%x的范围,y的初值
%plot(a,b(:,1))
clc,clear,close all;
a=1;%初始时刻
b=10;%结束时刻
n=100;%离散点数量
x0=1;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
y0=[1,10,30];
%计算
y(1,:)=y0';
for i=1:n %迭代
k1=feval('fun_3rd',x(i),y(i,:));
k1=k1';
k2=feval('fun_3rd',x(i)+h/2,y(i,:)+h*k1/2);
k2=k2';
k3=feval('fun_3rd',x(i)+h/2,y(i,:)+h*k2/2);
k3=k3';
k4=feval('fun_3rd',x(i)+h,y(i,:)+h*k3);
k4=k4';
y(i+1,:)=y(i,:)+h*(k1+2*k2+2*k3+k4)/6;
end
plot(x,y(:,1),'o');
改进欧拉方法:一阶问题
%向前欧拉法的改进方法
%改进欧拉方法
%一阶问题
clc,clear,close all;
a=0;%初始时刻
b=2*pi;%结束时刻
n=100;%离散点数量
x0=0;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
fun=inline('sin(x)+y','x','y');
y0=1;
%计算
y(1)=y0;
for i=1:n %迭代
k1=feval(fun,x(i),y(i));
k2=feval(fun,x(i)+h,y(i)+h);
y(i+1)=y(i)+h/2*(k1+k2);
end
plot(x,y,'o');
改进欧拉方法:高阶问题
%高阶问题
clc,clear,close all;
a=1;%初始时刻
b=10;%结束时刻
n=1000;%离散点数量
x0=1;%初值
h=(b-a)/n;%步长
x=x0 + [0:n]*h;%离散点数组
y0=[1,10,30];
%计算
y(1,:)=y0';
for i=1:n %迭代
f1=feval('fun_3rd',x(i),y(i,:));%x是标量,y是向量
f1=f1';
f2=feval('fun_3rd',x(i)+h,y(i,:)+h);
f2=f2';
y(i+1,:)=y(i,:)+h/2*(f1+f2);
end
plot(x,y(:,1),'o');%所有的行的第一列偏微分方程数值解:一维热传导方程

%偏微分方程数值解
%1.空间有多大
%2.时间有多长
%边界条件和初值
%显示向前欧拉算法
clc,clear,close all;
A=0.5;
xf=2;%边界点
T=0.1;%最后到达的时刻
M=50;%空间上分段,空间离散个数
N=100;%时间上分段,时间离散个数
fun0=inline('sin(pi*x)','x');%初值
bx0=inline('0');%左边界条件
bxf=inline('0');%右边界条件
dx=(xf-0)/M;%空间步长
dt=(T-0)/N;%时间步长
x=[0:M]'*dx;%空间离散点
t=[0:N]'*dt;%时间离散点
r=A*dt/dx/dx;
r1=1-2*r;
for i=1:M+1 %离散初始时刻的值
u(i,1)=feval(fun0,x(i));
end
for n=1:N+1 %边界条件
u([1,M+1],n)=[bx0(t(n));bxf(t(n))];
end
for k=1:N
for i=2:M
u(i,k+1)=r*(u(i+1,k)+u(i-1,k))+r1*u(i,k);
end
end
mesh(t,x,u)








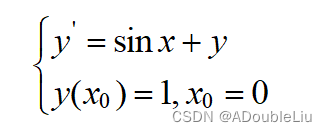















 654
654











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










