【LeetCode】547.省份数量(Number of Provinces)

题目描述

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the i^th city and the j^th city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

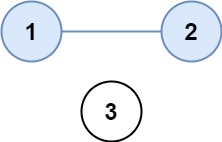
Input：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output：2

Example 2:

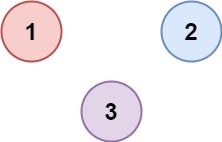
Input：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output：3

Constraints:

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] is 1 or 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

题目来源：https://leetcode-cn.com/problems/number-of-provinces/

题目大意

输入一个二维数组isConnected，若isConnected[i][j] = 1表明第$i$个城市和第$j$个城市是直接相连的，若isConnected[i][j] = 0表明第$i$个城市和第$j$个城市不是直接相连的。所有直接相连或间接相连的城市构成一个省，题目要求我们返回输入中省的数量。

解题方法

方法一：并查集

思路
根据本题题意，对于输入的$n\times n$二维矩阵isConnected，可构建出如下的图模型：

• 将每座城市看作图中的一个节点，分别用编号$0,\cdots ,n-1$来表示；
• 如果isConnected[i][j] = 1，则表明编号为$i$、$j$的节点之间存在一条无向边，无权值；
• 题目要求我们求解的省份数量，其实就是找出图中连通块的数量。

基于上述建立的图模型，本题可以用并查集来求解，而且可以直接套用朴素并查集的模板。编号$0,\cdots ,n-1$代表$n$个节点，使用一维数组$p$来存储并对这些节点进行初始化，然后遍历二维数组isConnected中的每个元素，isConnected[i][j] = 1则合并编号为$i$、$j$的节点，最后，统计数组$p$中满足 $p[x]==x$ 的个数并返回。并查集中只有根节点才会满足$p[x]==x$这一等式，根节点的个数就代表图中连通块的数量。

代码

class Solution {
    int[] p;

    public int find(int x){
        if(p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    public void union(int x, int y){
        p[find(x)] = find(y);
    }

    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        p = new int[n];
        for(int i = 0; i < n; i ++) p[i] = i;

        for(int i = 0; i < n; i ++){
            for(int j = 0; j < n; j ++){
                if(i != j && isConnected[i][j] == 1) union(i, j);
            }
        }

        int res = 0;
        for(int i = 0; i < n; i ++){
            if(p[i] == i) res ++;
        }
        return res;
    }
}

复杂度分析

• 时间复杂度：$O(n^{2}logn)$，其中$n$为节点（或城市）的数量，需要遍历isConnected中的所有元素，时间复杂度是$O(n^2)$，使用了路径压缩后，并查集操作的最坏时间复杂度是$O(logn)$（平均情况下的时间复杂度是$O(\alpha (n))$，其中$\alpha (n)$是一个很小的常数），因此总时间复杂度是$O(n^{2}logn)$。
• 空间复杂度：$O(n)$，其中$n$为节点（或城市）的数量，需要使用一维数组$p$来存储每个节点的父节点。