《Graph Neural Networks for TopologicalFeature Extraction in ECG Classification》论文阅读

最新推荐文章于 2025-05-17 22:15:01 发布

汤汤upup

最新推荐文章于 2025-05-17 22:15:01 发布

阅读量414

点赞数

分类专栏：论文翻译与学习文章标签： python matplotlib

本文链接：https://blog.csdn.net/m0_55245520/article/details/132580588

版权

论文翻译与学习专栏收录该内容

7 篇文章

订阅专栏

基于图神经网络的心电分类拓扑特征提取

论文地址：Graph Neural Networks for Topological Feature Extraction in ECG Classification | SpringerLink

代码地址：GitHub - KamyarZeinalipour/ts2g: Converting time-series to graph using three different method which are natural visibility graph, horizontal visibility graph, and quantile graph

一、摘要

心电图(ECG)是评估心血管系统功能的可靠仪器。最近，人们非常重视对心电图的精确分类。虽然心电情况有许多相似之处，但很少有人关注使用图神经网络对心电进行分类。在这项研究中，我们提供了三种不同的技术来分类心跳使用深度图神经网络来准确地分类心电信号。我们建议使用不同的方法从心电信号中提取拓扑特征，然后使用图神经网络的一个分支图同构网络对心电进行分类。在PTB Diagnostics数据集上，我们测试了这三种建议的技术。结果表明，三种方法对心律失常的分类预测准确率分别为99.38、98.76和91.93%。

二、介绍

心电图（ECG）一种可以使用特殊设备从人体监测的生物物理信号。它储存着关于心脏如何运作以及心脏是否受到异常状况影响的关键信息。心脏病专家和医疗从业者经常使用心电图检查心脏健康。与许多其他时间序列数据一样，识别和分类心电信号中各种波形和形态的困难是人工分析的根本问题。这项任务需要一个人花很长时间才能完成，而且容易出错。值得注意的是，准确检测心血管疾病至关重要，因为它们占全球所有死亡人数的三分之一左右。数以百万计的人患有心律不齐，这在某些情况下可能是致命的。因此，精确和低成本的心律不齐诊断是非常需要的。

文献中的许多研究都研究了利用机器学习方法来可靠地检测ECG数据中的异常，以克服人类分析所确定的挑战。这些方法大多包括的步骤如下：首先进行心电信号准备，然后从这些信号中获得手工特征，通常是信号窗口的统计汇总，并用于最终分类任务的后续分析。在基于计算机的应用中，已经使用了强大可靠的算法将心电信号分为两类或多类，其中包括模糊c-means、k近邻、深度神经网络、卷积神经网络、高阶统计量、朴素贝叶斯分类器、支持向量机、加权ELM。

本研究的主要贡献如下:

第一，我们提出结合不同的方法来开发一种新的心电分类方法。为此，我们使用三种不同的方法将心电信号转换成图，然后将结果图馈送到一个称为图同构网络(GIN)的图神经网络分支进行图分类。

第二，我们在一个众所周知的数据集(PTB Diagnostic ECG)上进行了实验比较，这证明了所提出方法的能力。

第三，我们共享了公共代码，用于使用我们将在本研究中讨论的不同方法将时间序列转换为图形;因此，其他研究人员可以跟随我们的脚步。

本文的其余部分安排如下:第二节提出了建议的方法，第三节展示了在ECG分类任务上建议的技术的实验，以及与文献中可比工作的比较，最后，第四节通过结论结束了本文。

三、方法

为了对心电信号进行分类，我们采用了三种变换方法，将时间序列变换为图；这些方法包括自然可见性图、水平可见性图和分位数图，然后将相应的图输入到图同构网络中，创建一个用于脑电图分类的模型。这是我们在调查中使用的全部步骤。

1、从时间序列到复杂网络

在这一部分中，我们描述了在我们的研究中实现的复杂网络的时间序列映射方法的文献中取得的关键结果。这些映射方法基于可见性概念和转换概率。

（1）自然可见图

Lacasa等人最初在2008年基于可见性原则提出了第一个将时间序列转换成图的解决方案。这种方法被称为自然可见性图(Natural Visibility Graph, NVG)，图中的每个节点对应于同一序列的时间序列数据，如果在各自的数据点之间存在一条可见性线，即在时间序列中，如果在两个对应的数据点之间可能画出一条直线，且不截取时间序列中两个数据点之间的数据“高度”，则两个节点相连。这种方法是建立在假设每个时间序列数据被认为是高度等于相应的数值同时当检查其他数据时，顶部的一部分可见。我们把时间序列中的每个数据看作图中的节点，如果在垂直平面内其中一个相对于另一个数据可见，则他们之间有边相连，也就是说，如果两个柱状图的顶部有一条直线，不与其他柱状图相交。一个时间序列与生成的网络的映射例子如图左侧图2.1所示，序列中的每个数据对应一个网络节点，如果其关联的数据高度满足Eq. 2.1可见性条件，则两个节点连接，另一方面，时间序列图中的蓝线表示可见性线(以及图中的连接)，如图所示，生成的图包含与时间序列数据(观测)数量相同的顶点。形式上，每个顶点都是一个观测值(ta, ya)，两个节点(ta, ya)和(tb, yb)是链接的(具有可见性)。如果ta < tc < tb的任何附加观测值(tc, yc)满足:

$y_c<y_b+(y_a-y_b)\frac{t_b-t_c}{t_c-t_a}$

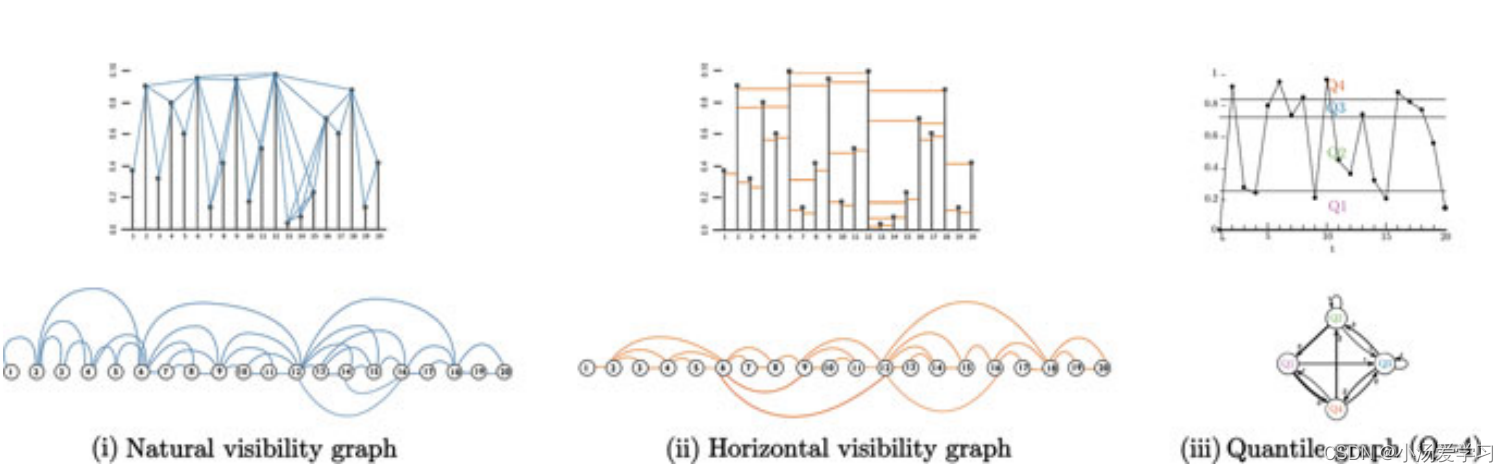
此图包括三个时间序列及其对应的图形，演示了将时间序列转换为图形的不同技术。玩具时间序列在图的上半部分，对应的图形在图的下半部分

（2）水平可见图

Luque等人在2009年提出了一种更直接的技术，称为水平可见性图(HVG)，以降低NVG相关的计算成本。根据该方法，如果可以在时间序列中绘制一条水平线，将两个数据对应的两条竖线连接起来，且不截取中间数据的任何高度，则在此选项中连接图中的两个节点。我们在图2.1的中间部分展示了该算法的基本演示，使用玩具时间序列和由此产生的水平可见性图;橙色线表示所有观测值之间的水平可见性线，序列中的每个数据对应一个图节点，如果两个节点对应的数据高度大于它们之间所有数据高度的总和，则两个节点相连。形式上，如果满足以下条件，两个节点(ta, ya)和(tb, yb)被链接并且是水平可见的。

$y_a,y_b>y_c$

对于所有使ta < tc < tb的tc。

（3）分位图

Campanaro等于2011年提出了分位数图(QG)。该方法不同于以往的可视性方法，它收集了相关的时间序列信息，如随时间的振荡。时间序列被分成Q个分位数，q1, q2，…qQ，每个分位数qi代表网络中的一个网络节点vi。因此，图的节点数量与分位数的数量相同。一个加权有向链接(va, vb, w(A,b))连接两个顶点va和vb，其中权重w(A,b)反映了来自分位数qa的观测值(tn, yn)之后是来自分位数qb的观测值(t(n+1)， y(n+1))的次数。

形式上，设M是时间序列X∈T到图g∈g的过渡，其中X = {X (T)| T∈N, X (T)∈R}， g = V, E分别是节点(顶点)V和边E的集合。假设X的基本离散化不受其值分布的影响。对X进行排序并在Q−1个区间内打破该排序，确定时间序列的Q个分位数，该分位数由将X划分为Q−1个等大小区间的切点定义。每个分位数的定义如下:

$q_i=x(\frac{T*i}{Q})$

考虑i = 1,2，…， Q每个X值映射到相关联的qi，对于i = 1,2，…一旦Q的分位数确定，然后将相关网络的节点vi∈V分配给每个分位数qi。在一个加权弧 $(v_i,v_j,w_{(i,j)}^k)\in E$ 的网络中，当存在qi和qj的两个值x(t)和x(t + 1)时，两个节点vi和vj通过E连接，其中qi和qj的值t = 1,2，…， T，其中k为时差k = 1，…， kMax，在本研究中我们考虑时差等于1的情况。加权有向邻接矩阵中的每个权值wk (i,j)，记为AK，是分位数中某个值在时间t时qi出现的次数，之后是分位数qj在时间t + k时的一个点。因此，沿着同一弧线的连续过渡会提高相关权值。加权有向邻接矩阵AK经过充分归一化后形成马尔可夫转移矩阵WK，其中 $\sum w_{(i,j)}^k=1$ 。在图2.1的右侧，我们使用一个玩具时间序列来描述这个投影和相关的网络;从T = 20个时间点，Q = 4个分位数的均匀白噪声X来说明。在时间序列图中，不同的颜色反映了与不同分位数相关的区域。分位数之间的重复转换导致图边的权重越大，线越粗。

2、图同构网络

在本文中，对于图分类任务，我们使用图神经网络的一个分支图同构网络(GIN) ；图同构网络的灵感来自于Weisfeiler-Lehman检验与图神经网络之间的紧密联系，Weisfeiler-Lehman检验是一种有效的判别一大类图的检验。假设G = (V, E)是一个图，其节点特征向量为Xv。对于v∈V，节点分类和图分类是图中特别感兴趣的两个组成部分，在本研究中我们应用了图分类任务，其中给定一组图 $\{G_1,...G_N\}$ 以及他们的标签 $\{y_1...y_N\}$ 如果目标是学习一个表示hG，它有助于预测整个图的标签yG = f (hG)。图神经网络学习一个节点hv和hG的表示向量，该表示向量是基于图的拓扑结构和节点特征Xv的整个图的表示向量。现代gnn使用邻域聚合方法，通过聚合其邻居的表示来更新节点的表示迭代；经过k次聚合迭代后，节点k−hop网络邻域的结构信息被包含在其表示中。通过将其作为可学习参数或固定标量，GIN以以下方式更新节点表示:

其中 $h_v^{(k)}$ 表示第k次迭代层的节点v特征向量。我们指定 $h_v^{(0)}=X_v$ 作为起始值，N(v)是与v相邻的一组节点。GIN的节点嵌入可以直接用于节点分类、链路预测和图分类等任务。研究者为图分类任务提出了如下的读出函数，该函数从单个节点嵌入创建整个图的嵌入:

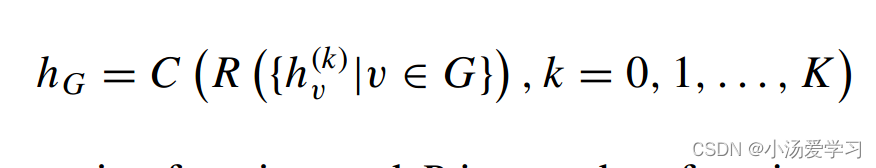
其中C是连接函数，R是读出函数。

四、实验

在本研究中，我们使用PTB诊断心电图数据库作为标记心电图记录的数据源。在我们所有的研究中，我们使用ECG导联II重新采样到125 Hz的采样频率作为输入。PTB诊断数据集包含290人的心电图记录，其中148人被诊断为心肌梗死(MI)， 52人是健康样本，其余的人患有其他七种疾病。在每个记录中以1000 Hz的频率捕获12个导联的ECG信号。在本研究中，我们使用预处理的PTB诊断心电图数据。本文提出了一种简单而有效的心电信号预处理方法，该方法涉及使用输入心电拍。从心电信号中提取心跳的步骤如下:

1. 将连续心电信号分割为10s窗口长度，选择一个10s窗口长度。

2. 将0-1范围内的幅值归一化。

3.借助一阶导数的过零点定位局部最大值的集合。

4. 在局部最大值的标准化值上使用0.9的阈值来找到可能的r -峰值候选集。

5. 计算R-R时间间隔的中位数作为窗口(T)的标称心跳周期。

6. 对于每个r峰，选择一个长度为1.2 T的信号部分。

7. 用零填充每个选定的部分到预定义的固定长度。

值得注意的是，该方法在从不同形态的信号中提取R-R区间方面非常成功。此外，它还能够准确识别心率的变化，这是心电信号分析的关键一步。对于异常样本的数量远远超过正常样本，我们通过简单地复制和粘贴正常数据来复制正常样本，以解决图神经网络预测更大样本类别的倾向。本文提出的方法的第一个任务是将心电信号转换成复杂的网络。

我们为研究中的心电信号创建了三种不同类型的复杂网络。第一种方法是自然可见图(NVG)，第二种方法是水平可见图(HVG)，分位数图(QG)是我们用来将心电信号转换为图的第三种方法，此外，应用分位数图方法，我们必须为这一步选择分位数的数量。因此，我们使用整个数据集将时间序列转换成2 ~ 30个不同分位数的分位数图，并将图输入到图同构网络中，然后选出性能最好的分位数，我们的研究取q = 24。图2.2给出了一个心电信号的例子，当分位数数为24时，它的自然可见度图、水平可见度图和分位数图如图2.2所示。在第二阶段，我们尝试训练一个对时间序列对应图进行分类的模型，并将转换后的时间序列图输入到一个名为图同构网络的图神经网络中，开发一个对时间序列对应图进行分类的模型。

所有的实验都是在Python中进行的；为了使用上述三种方法将时间序列转换为图形，我们用Python开发了一个应用程序。我们利用[16]作者发布的官方图同构网络(GIN)软件对图进行分类。我们对图同构网络(GIN)(公式2.4和2.5)的模型和图分类任务的配置进行了评估。随后，我们实现LIB-SVM进行10倍交叉验证。在交叉验证中，我们给出了整个10倍的平均验证精度。5到8个GNN层(由输入层组成)应用于所有设置，所有mlp都有两个层。每个隐藏层都经过批处理归一化[22]，并使用Adam优化器，初始学习率为0.01，每50个epoch学习率下降0.5。超参数调优如下，隐藏神经元个数为64个，批大小为32、64、128个，密集层后的dropout ratio为0 ~ 0.5，epoch数为300 ~ 400。选择交叉验证精度在10倍平均值上最大的历元。在图2.3中，我们绘制了使用本研究中使用的不同变换方法训练的训练集性能。

训练集性能与每个提出的方法相关联。我们可以看到NVG和HVG在训练集上都比QG-24有更好的表现，NVG和HVG几乎可以完美的拟合训练集

表2.1将本文中描述的实验与文献中使用我们在调查中使用的相同数据集解决相同分类问题的其他方法进行了比较。

我们可以看到，使用NVG图的方法性能最高，准确率为99.38%，其次是使用HVG图的方法，准确率为98.76%，第三是使用QG-24的方法，准确率为91.93%。因此，我们可以得出结论，该方法适用于心电信号的分类。

五、总结

我们的主要贡献是建议使用不同的NVG、HVG和QG集成映射方法，创建一个更丰富的特征集，定义一个时间序列，通过实现一个名为图同构网络的图神经网络，使用相关的复杂网络对时间序列进行分类。从本文得到的结果可以得出结论，这些不同的映射技术可以有效地用于使用图同构网络对心电信号进行分类。这是第一次进行如此全面和系统的调查。通过在实验中使用图同构网络，我们可以从本文的研究结果中推断出这种映射方法可以适当地用于心电信号的分类。在本文中，我们尝试将时间序列映射到自然可见性图、水平可见性图和分位数图，然后将这些图输入到图同构网络中，以便对心电信号进行分类。第一种方法使用NVG图获得了99.38%的准确率，第二种方法使用HVG图获得了98.76%的准确率，第三种方法QG-24获得了91.93%的准确率。未来的研究可以考察其他gnn在心电信号分类方面的表现。当前的单变量映射可以推广到多变量设置。例如，我们可以研究多层复杂网络，它允许多个不同的变量(例如，ECG和EEG信号可以在同一网络的单独层上表示)和空间特征在单个复杂网络中组合;之后，我们可以使用图神经网络对两个或多个时间序列的组合进行分类。另一方面，该方法也可以应用于时间序列分类中的其他任务，如语音识别。