【蓝桥杯准备打卡-基础算法笔记DP篇】-2.【完全背包】

1.问题描述：

有 N种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

2.问题的解决思路：

2.0 思路概要

前面说过解决dp问题的关键在于 状态表示和状态计算，我们逐步分析解决。

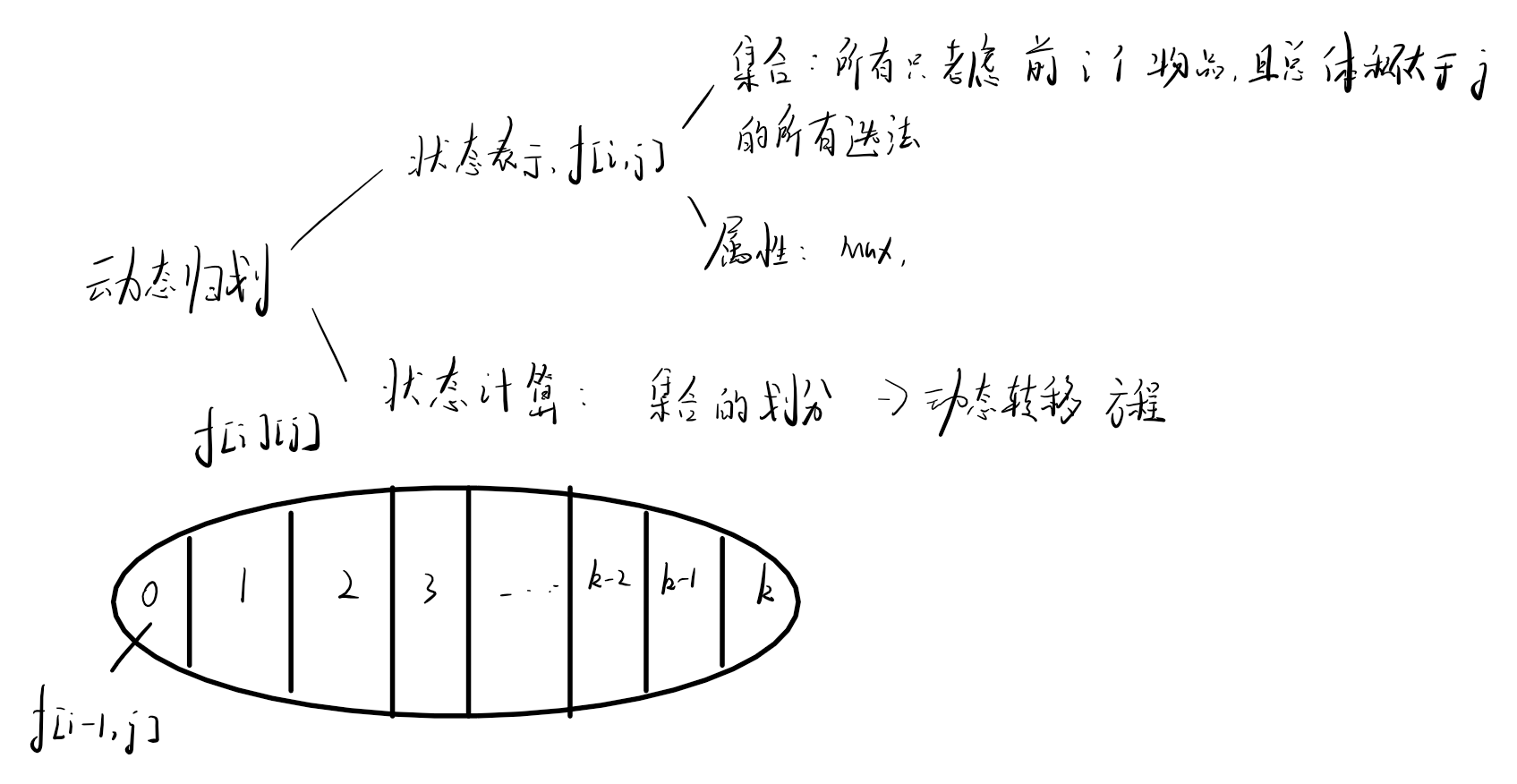
2.1 状态表示

状态表示 可以 分栏为 集合定义以及集合属性

集合定义： 根据题意，我们规定集合dp【i】【j】表示 所有只从前0到i种物品种选，而且总体积 不大于j的选法

集合属性：我们定义集合的属性值 为 满足上述要求的集合所有选法中，造成背包价值最大的选法。

2.2 状态计算

集合的划分：

我们把集合dp 【i】【j】划分为** k+1**个子集，分别表示 背包种 所拥有 第 i 种 物品的数量

子集的表示：

其中，绿色 框 所表示的 子集意义 则为 所有只从前0到i种物品种选，而且总体积 不大于j的所有选法，这一前提下，**不包含第i种物品的选法 **，也就是 **所有只从前0到i-1种物品种选，而且总体积 不大于j的所有选法，根据集合定义，我们得知 **绿色 子集表示为 dp[i-1][j]**

最右侧的 紫色框 表示集合 意义为 所有只从前0到i种物品种选，而且总体积 不大于j的所有选法，这一前提下，包含第i种物品选了k次 的选法 **

我们依然采取曲线救国的方式：从紫色 集合 中 同时去除 k个第i种 物品，则这个时候可以紫色框 根据 状态定义，可以表示为

dp[i-1][j - k*v[i] ]

而 这个集合的 属性值（所有选法中的背包最大价值）和去除 物品之前，相差了 第i个物品价值的 k 倍 也就是 k*w[i],那么紫色 集合 泛指的包含k个第 i种个物品集合的选法中最大价值可以表示成

**dp[i-1][j - k*v[i] ]+ k*w[i]**

动态转移方程

容易想到 背包中能塞入 第i种 物品 的数量 k倍,其不难超过当前规定的背包体积j，满足方程

kv[i]<=j

显然 原 集合** dp[i][j] = max{dp[i-1][j - kv[i] ]+ kw[i] | kv[i]<=j}**

3.代码和转移方程的优化

3.1 朴素版本，时间复杂度O(nm2)

#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int dp[N][N], v[N], w[N];
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k * v[i] <= j; k ++ )
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
    cout << dp[n][m] << endl;

3.2 状态转移方程的优化

思想一：代数优化

dp[i][j] = max{dp[i-1][j - kv[i] ]+ kw[i] | kv[i]<=j}

扩展开来（下面的等于号不是 属性值意义上的等于，仅表示集合的组成，不严谨，能看懂就行）

dp[i][j]=dp[i-1][j ]+dp[i-1][j - v[i] ]+ w[i] + dp[i-1][j - kv[i] ]+ kw[i] + dp[i-1][j - 2v[i] ]+ 2w[i] .....+{dp[i-1][j - kv[i] ]+ kw[i]

同理，我们可以知道dp[i][j-v[i]] 也可以拆解成 （为什么要拆这个，这就是代数优化比较玄学的地方了，想不到，易理解）

dp[i][j-v[i]]=dp[i-1][j - v[i] ]+ w[i] + dp[i-1][j - kv[i] ]+ kw[i] + dp[i-1][j - 2v[i] ]+ 2w[i] .....+{dp[i-1][j - kv[i] ]+ k*w[i]

关于为什么刚好只差一项，因为两个方程中的k 分别满足， k v[i]<=j 以及 kv[i]<=j - v[i] ，这时候 k的最大值差距为1

如下图所示

思想二：递推图

我们同样可以换一种方式去理解，

根据状态转移方程 我们可以知道 ，dp【i】【j】所表示的 框 由 其上方 黄色框 最大值和其左上方 所有蓝色框+对应的k倍 价值 的最大值 中 的最大值 为 红色框的属性值，对吧

而上图中蓝色框中的最大值，恰巧表示下图绿色框的值

显然，优化的核心，在于我们利用了 以及前面得到了计算结果，因为 解决朴素版本题目代码 在计算 红色框 之前，我们一定要先求出 绿色框，而 我们求红色框的时候 ，又要重新比较k个蓝色， 这是不必要的，我们只需呀拿 绿色框 比较即可，他象征了 k个蓝框的最大值 了。

根据以上两个思路 ，我们都可以得到 优化后的状态转移方程：

dp[i][j] = max{dp[i][j -v[i]] +w[i], dp[i-1][j] }

3.3 二维到一维 ：滚动数组优化自我滚动

和01背包如出一辙，我们可以发现每次跟新的值 有且 仅根当前这一排的 和前一排 的属性值有关联，所以，可以优化为一维数组

dp[j] = max{dp[j -v[i]] , dp[j] }

3.4 采用正序循环 的解释

为什么01背包 是逆序循环，而 完全背包是正序循环呢，我们罗列一下 状态转移方程

01背包： dp[j] = max{dp[j -v[i] ] + w[i] , dp[j] }

完全背包：dp[j] = max{dp[j -v[i] ] + w[i] , dp[j] }

好像一样是么，那么他们的区别就在于循环顺序了，为什么?

其实 二维 优化到 一维 也就导致 我们 循环顺序的改变，那么我们看看一维化前的状态转移方程对比

01背包： dp[i][j] = max{dp[i-1][j -v[i]] +w[i], dp[i-1][j] }

完全背包：dp[i][j] = max{dp[i][j -v[i]] +w[i], dp[i-1][j] }

发现了微妙的不同吧，我们用图片清晰的描述一下

你看，鄙人前一篇文章讲述了01背包为何 逆序，我们这边讲讲 为什么 完全背包 不能逆序

逆序的话，我们红框 的值 由 绿色框 和黄色 决定，但是绿色框 的属性 我们还没有计算出来，所以不能逆序，只能正序来依次地推

3.5 代码参考

#include<iostream>
using namespace std;

const int N = 1010;

int n, m;
int dp[N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ){
        int v, w;
        cin >> v >> w;
        for(int j = v; j <= m; j ++ ){
                dp[j] = max(dp[j], dp[j - v] + w);
        }
    }
    cout << dp[m] << endl;
}